基于Hermite插值的高精度数值积分公式

龙爱芳，胡军浩

（中南民族大学 数学与统计学学院，湖北 武汉430074）

随着科学的进步，计算机技术的发展，很多领域涉及到定积分的计算，因此研究高精度的数值积分公式是有实际意义的.数值积分常见的有梯形公式和Simpson公式，它们的计算虽无需提供导数值，但代数精度不高.梯形公式有一次代数精度，Simpson公式有3次代数精度［1-6］.文献［7-8］虽给出一个高精度的数值求积公式，但必须提供求积节点的一阶导数值.文献［9］给出了Newton-cotes求积公式的渐近性，虽可大大提高数值求积公式的代数精度，但同样必须提供n+1阶导数值，文献［10］的求积公式没有承袭性.本文从Hermite插值多项式出发，构造了具有误差量级为O（h5），且不需要计算导数值，只需要提供求积节点函数值的高精度数值求积公式.

1 高精度数值求积公式

1.1 Hermite插值多项式的构造

构造满足插值条件f（xk）＝p（xk），f（xk+1）＝p（xk+1），f′（xk）＝p′（xk），f′（xk+1）＝p′（xk+1）次数不超过3的Hermite插值多项式的p（x）.即

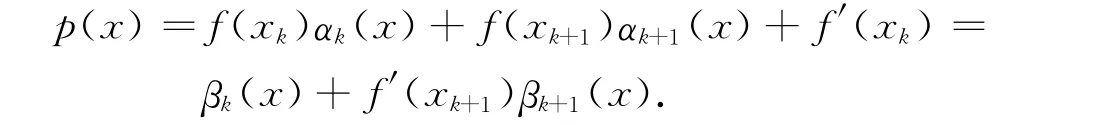
上式中：αk（x），αk+1（x），βk（x），βk+1（x）为插值基函数，它们分别满足

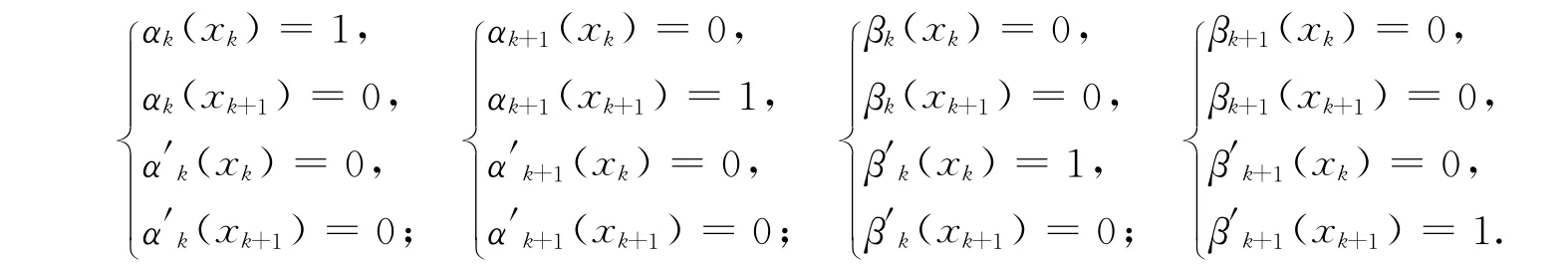
αk（x），αk+1（x），βk（x），βk+1（x）的表达式分别为

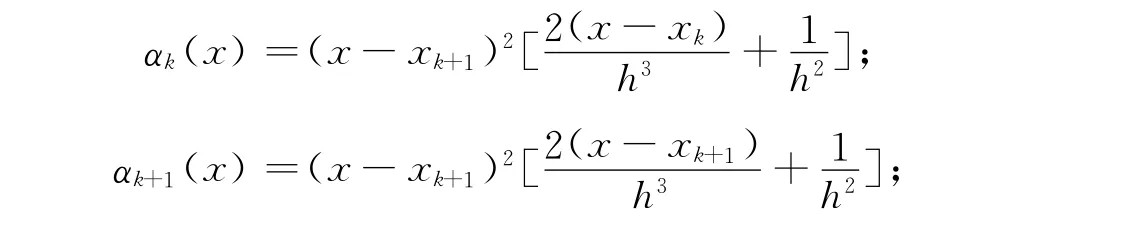
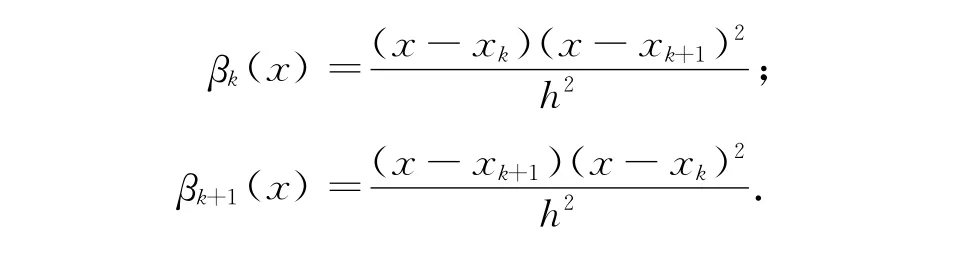
其中：h＝xk+1-xk.

构造的插值多项式余项表达式为

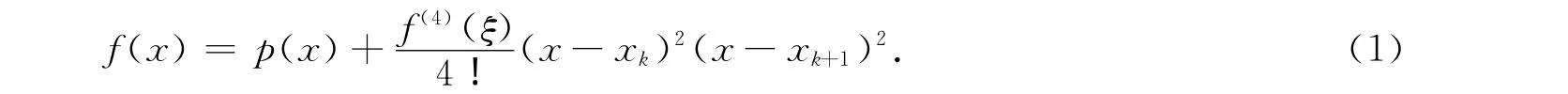
式（1）中：ξ在xk与xk+1之间，并且与x有关.

1.2 数值求积公式的构造

对式（1）两边求积分，应用广义积分中值定理，可得到积分中值定理.

定理1 设函数f（x）在区间［x，xk+1］有4阶连续导函数，则

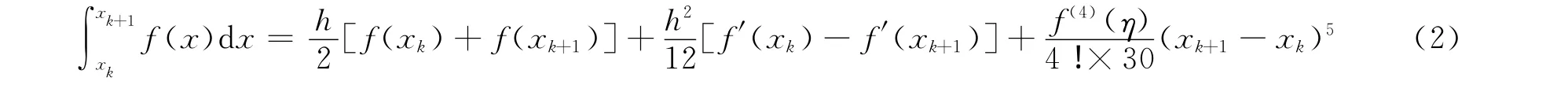
成立，η在xk与xk+1之间.

由式（2）得到带有一阶导数的数值求积分公式，即

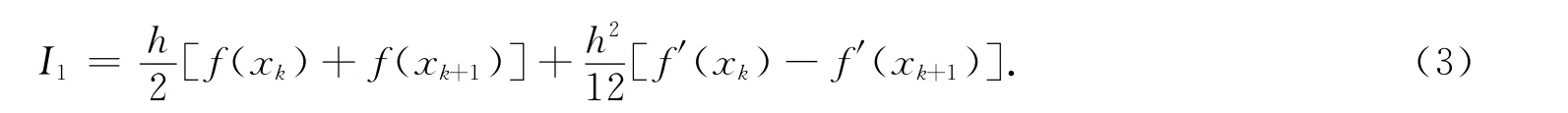
由式（2）可知，数值求积公式（3）具有3次代数精度.在式（2）中，令xk＝a，xk+1＝x，则有

为了提高数值求积公式的代数精度，分析定理1中间点η的渐近性，则可得到定理2.

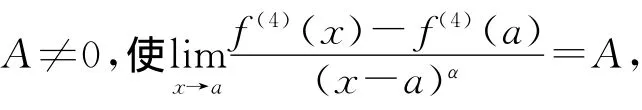
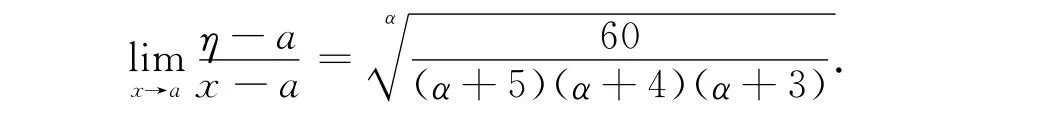
证明 令

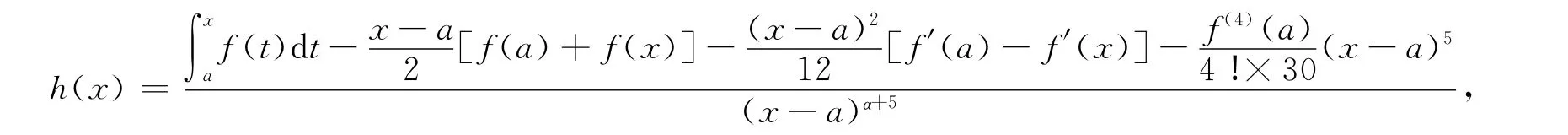
应用3次洛必达法可得

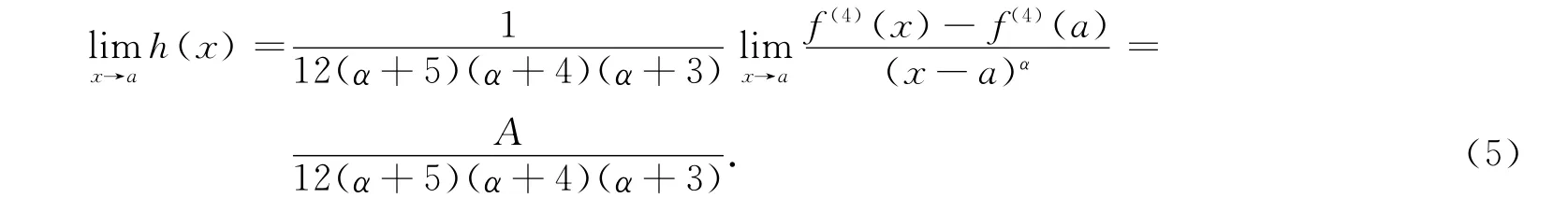
应用式（4）可得

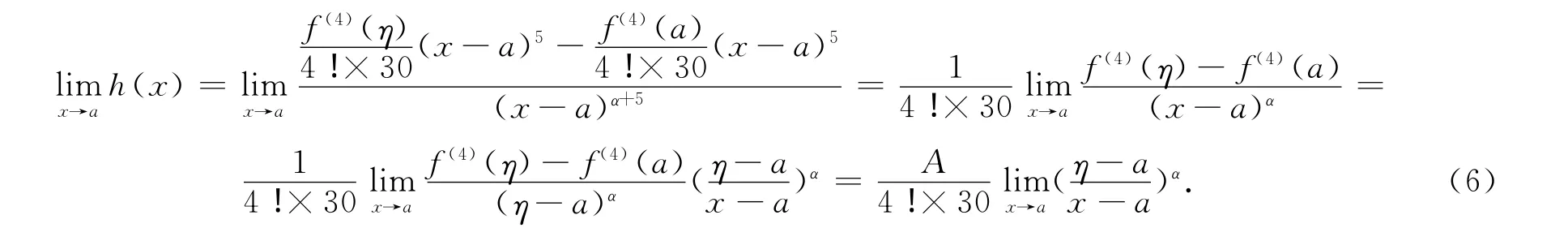
应用式（5），（6）可得

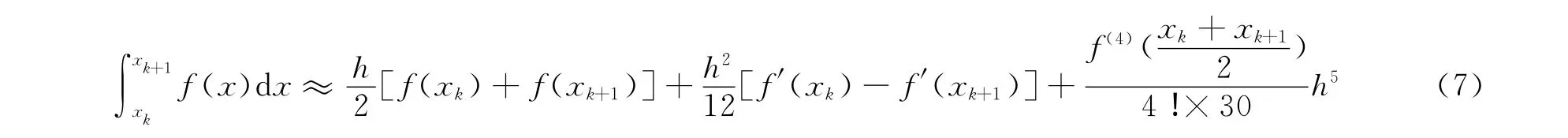
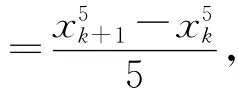
由式（7），可得到具有5次代数精度的第2个数值求积公式，记为

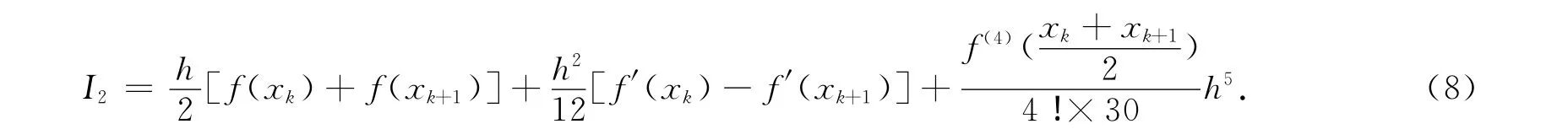
应用复化求积得

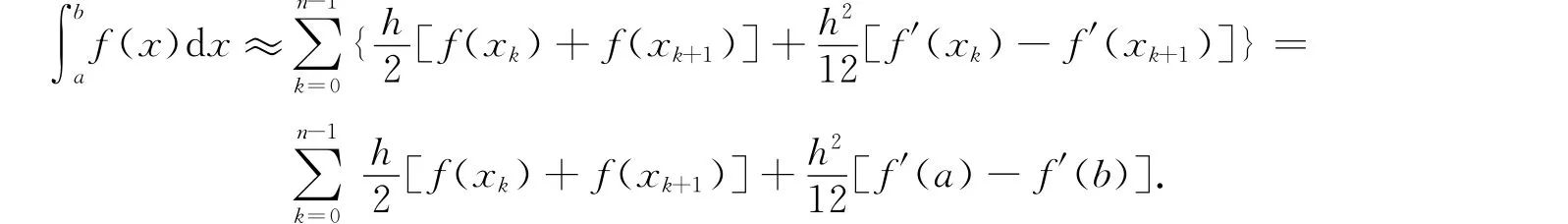
为了避免求导数，对上式的数值求积公式进行修正，应用公式

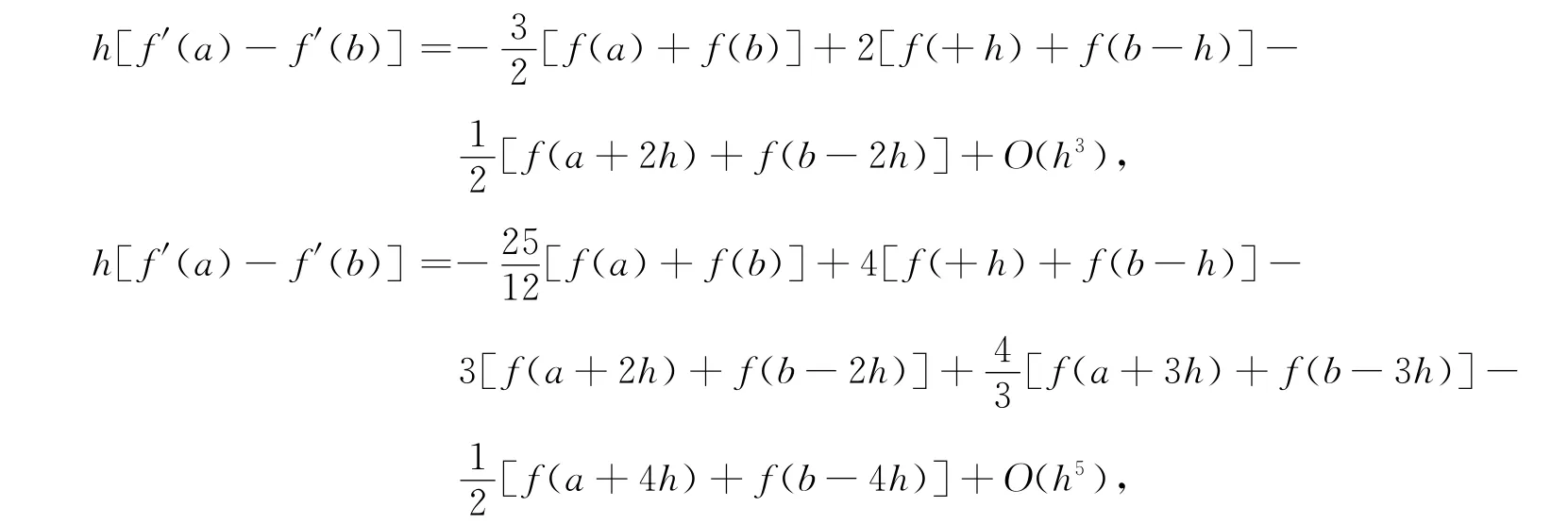
得到只需计算求积节点函数值，无须提供求积节点导数值的两个数值求积公式，分别为

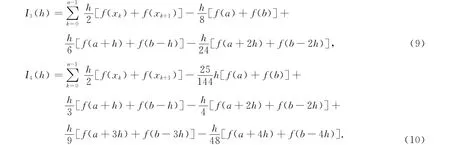
公式（9），（10）的误差量级分别为O（h4），O（h5）.

2 数值试验

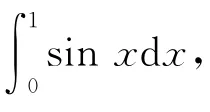
应用梯形公式、求积公式（3），（8）计算，计算结果如表1所示.应用复化梯形公式、求积公式（9），（10）计算，计算结果如表2所示.

表1 梯形公式、求积公式（3），（8）的计算结果Tab.1 Numerical experiment of trapeziod formula and formula（3），（8）

表2 复化梯形公式，求积公式（9），（10）的计算结果Tab.2 Numerical experiment of compound trapeziod formula and formula（9），（10）

从计算结果看，公式（3）与公式（8）比梯形公式的精度高很多，但必须提供一阶导数或四阶导数；而公式（9）和公式（10），却不用计算导数，计算的节点函数值的个数与复化梯形公式一样.因此，计算量与复化梯形公式相当.复化梯形公式的误差量级为O（h2），而公式（9）的误差量级为O（h4），公式（10）的误差量级为O（h5）.因此，公式（9）和公式（10）是非常有效的，无须计算导数的两个数值积分公式.

［1］ 李庆杨.数值分析［M］.武汉：华中科技大学出版社，1986：83-106.

［2］ 李庆杨.数值计算原理［M］.北京：清华大学出版社，2000：251-282.

［3］ 李毅夫.Simpson公式余项中间点渐进性定理及Simpson公式的改进［J］.贵州师范大学学报：自然科学版，2007，25（4）：67-69.

［4］ 程海来.关于Simpson公式的两点注记［J］.数学的实践与认识，2007，27（21）：91-93.

［5］ 杜跃鹏，肖泽昌.改进Simpson公式及误差分析［J］.高师理科学刊，2008，28（4）：27-29.

［6］ 刘彬清.一类高斯求积公式的极限性质［J］.工程数学学报，2003，20（4）：137-139.

［7］ 吴新元.一个高精度数值积分公式［J］.计算物理，1988，5（4）：473-477.

［8］ 郑华盛.高精度数值积分公式的构造及其应用［J］.数学的实践与认识，2007，37（15）：141-148.

［9］ 刘彬清.Newton-cotes数值求积公式的渐近性［J］.上海大学学报：自然科学版，2002，8（6）：503-506.

［10］ 刘彬清.一类高斯求积公式的极限性质［J］.工程数学学报，2003，20（4）：137-139.