三阶微分方程的Legendre-Petrov-Galerkin谱元方法

吴胜，庄清渠

（华侨大学 数学科学学院，福建 泉州362021）

作为数值求解偏微分方程的3大主要方法之一，谱元方法由于具有高精度，及对复杂区域的适应性的优点，已经被广泛应用于分子动力学模拟、复杂流体计算、量子计算、电磁场计算和数值天气预报等领域［1-7］.文献［8-9］分别研究了四阶微分方程的谱方法和谱元法.文献［10］用Legendre-Petrov-Galerkin和Chebyshev配点法求解三阶微分方程，由于配点法强烈依靠选取的配置点，容易产生数值不稳定的现象.文献［11］则利用对偶Petrov-Galerkin法求解三阶微分方程.文献［12］使用Petrov-Galerkin方法对修正的KdV方程进行数值求解.文献［13］用有限差分方法和Chebyshev方法求解带边值条件的KdV方程，数值结果表明Chebyshev方法是比较有效的.文献［14］研究了KdV方程的多区域Legendre-Petrov-Galerkin谱元方法，其实质是带时间三阶方程的谱元法，然而，其数值结果用的都是两区域的计算，并不是真正的谱元法计算，也没有具体的计算过程.本文研究三阶微分方程的Legendre-Petrov-Galerkin谱元法，主要考虑方程的数值计算.

1 格式的建立

记Λ＝（-1，1），考虑如下的三阶微分方程

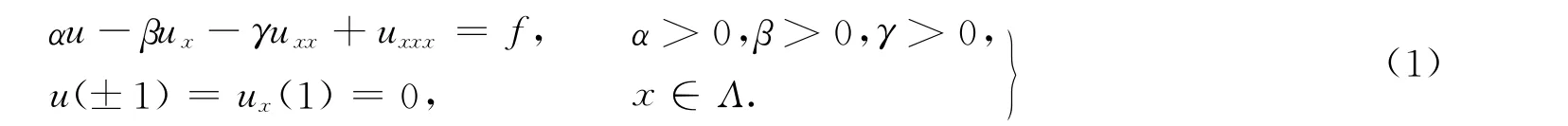
为了用Legendre-Galerkin谱元法对该问题进行数值逼近，需要将区间Λ剖分成K（K≥2）个子区间，即

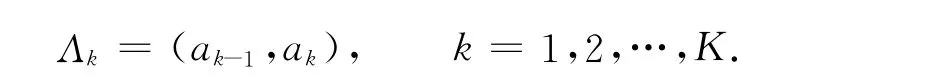
上式中：-1＝a0＜a1＜…＜aK＝1.

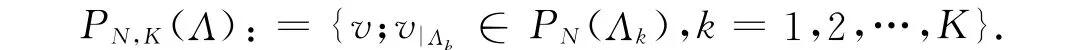
上式中：PN（Λk）表示在Λk上次数不超过N的全体多项式所组成的空间.用¯N表示离散参数（N，K），定义试探函数空间和检验函数空间为

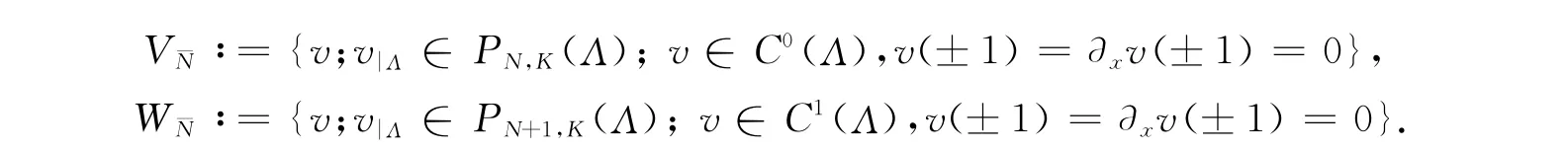
为了方便表达，对任意的1≤p≤∞，定义Lp（Λ）＝｛v；‖v‖Lp＜∞｝，其中

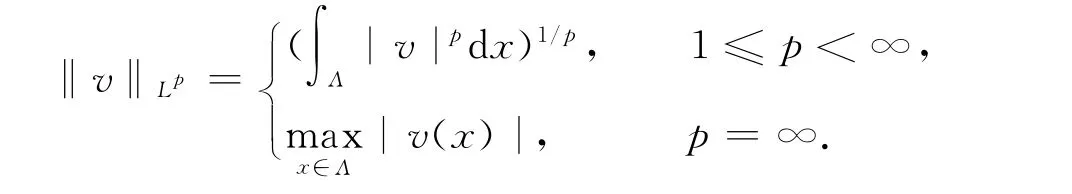
其中：（·，·），‖·‖和｜·｜分别表示空间L2（Λ）的内积、范数和半范，（u，v）＝∫Λu（x）v（x）dx.问题（1）的Legendre-Petrov-Galerkin谱元逼近形式为：找∈，使得

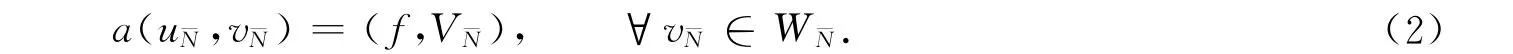
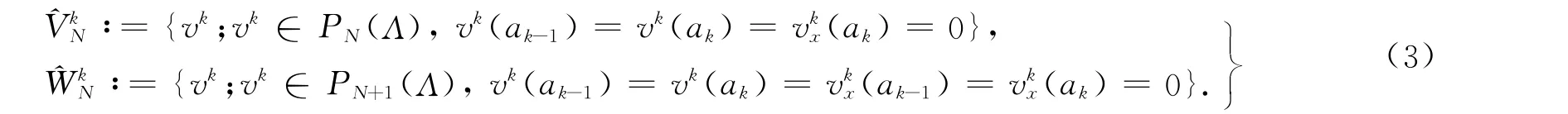
当j＝0，1，…，N-3；k＝1，2，…，K，基函数定义为

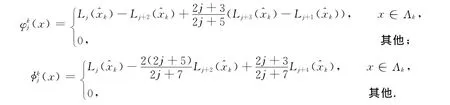
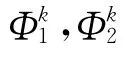
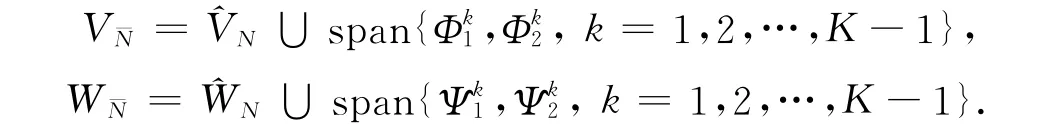
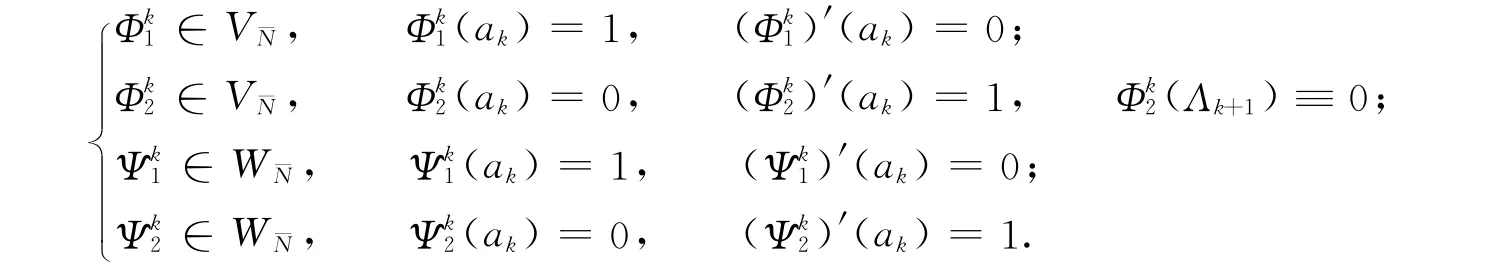
通过验证可知函数

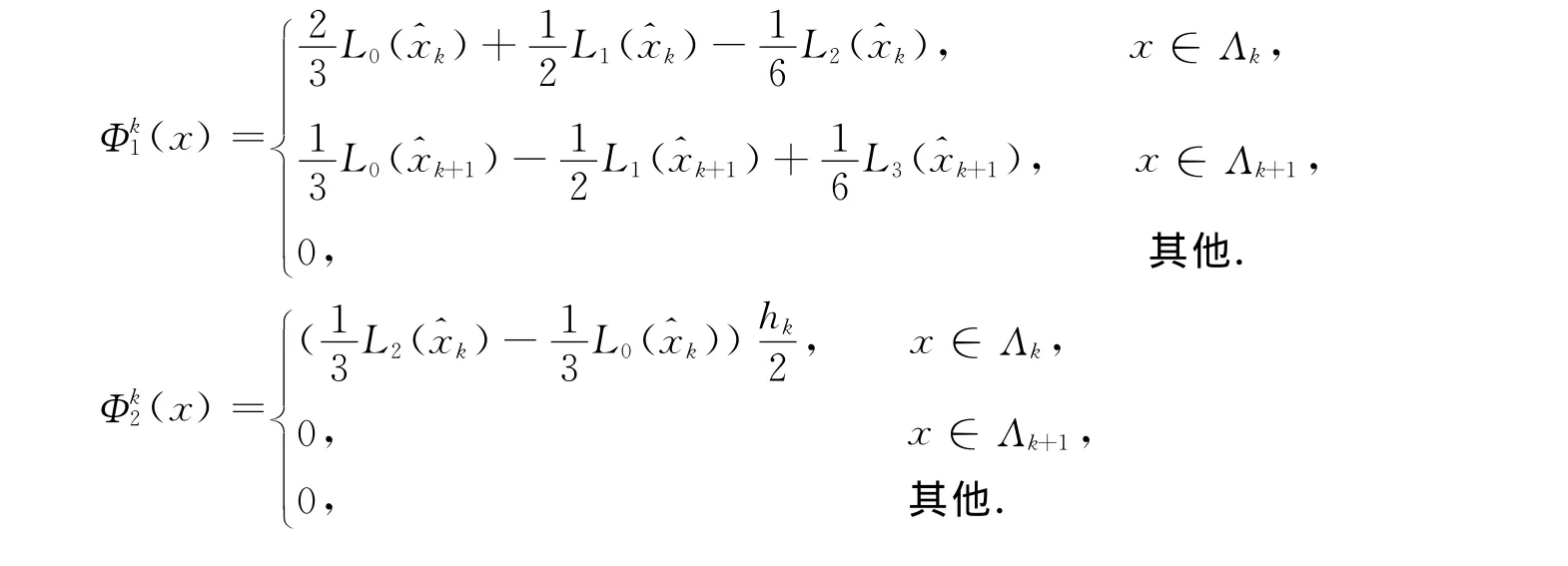
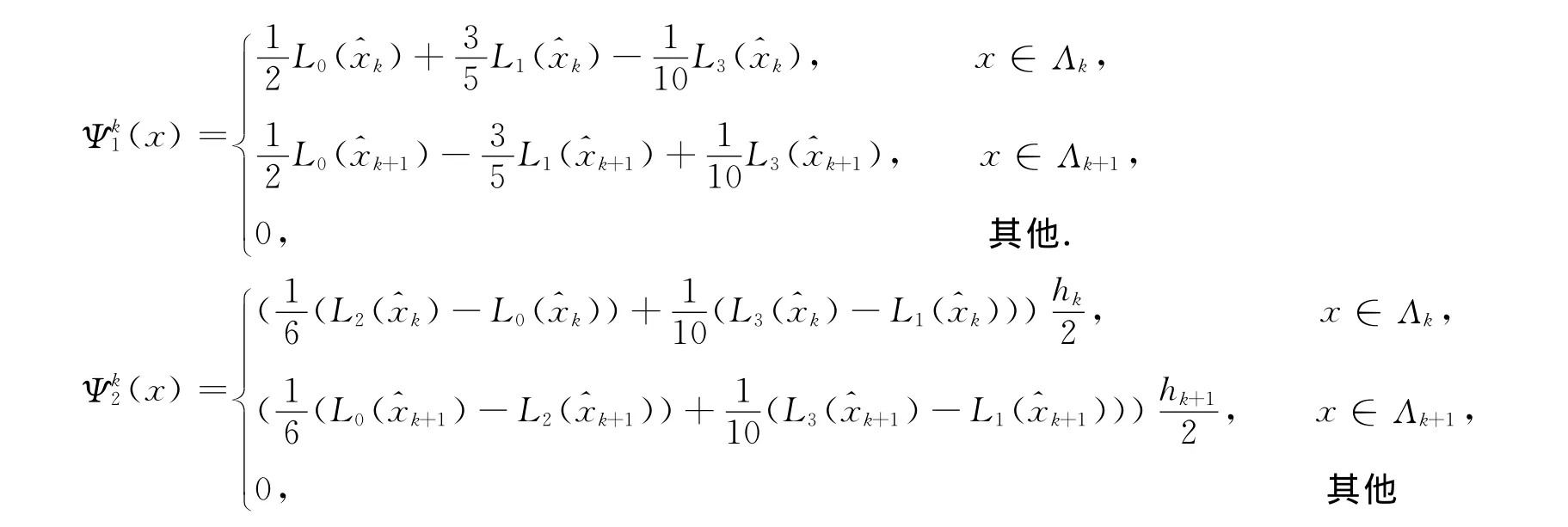
满足所要求的条件，其中：k＝1，2，…，K-1.

最后，将文献［9］用于求解四阶方程的Legendre谱元逼近法的计算思想推广到式（2）的计算中，详细计算过程有以下4个步骤.

1）构造关于双线性形式a（·，·）的正交补.令，∈是问题的解则和在a（·，·）意义下是正交的，即

2）求解各子区间内部节点上的子问题，找＾u¯N∈＾V¯N，使得

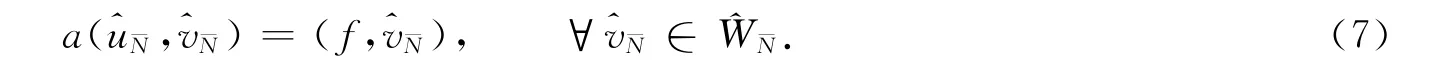
3）求解单元交界节点处的子问题，即求（，）（i＝1，2，…，K-1），

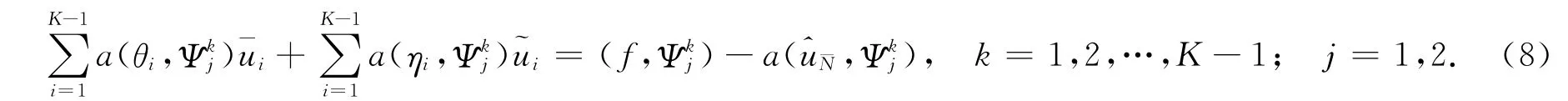
4）由式（7），（8）可得

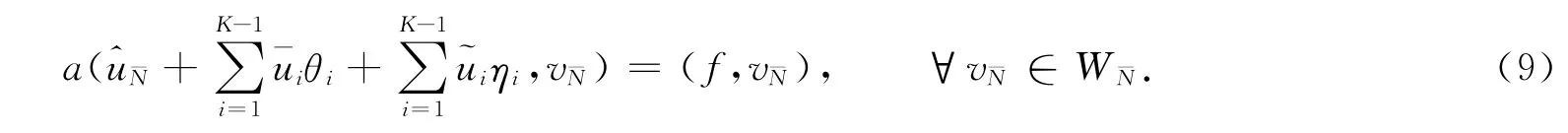
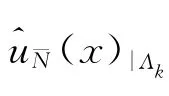
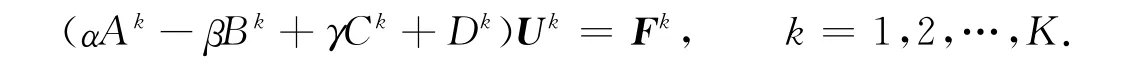
式（6）所对应的线性系统也可类似表达.

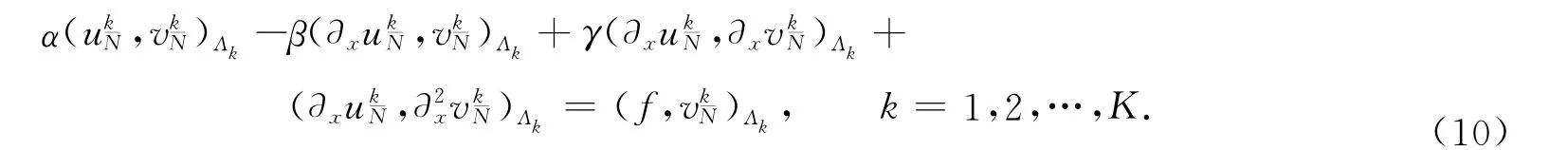
具有唯一解，而且解满足

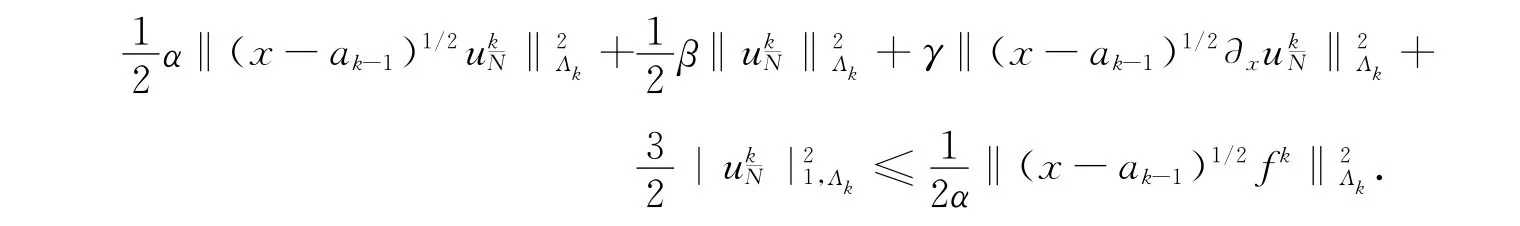
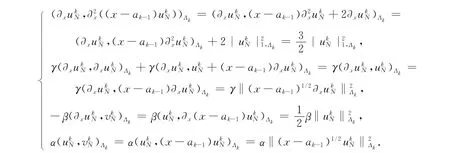
由三角不等式，可得

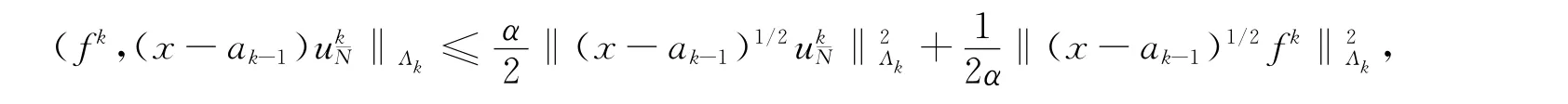
利用Lax-Milgram引理，可知结论成立.

2 数值实验

下面给出一个数值例子说明Legendre-Petrov-Gelarkin谱元逼近形式（2）的精度及有效性，在问题（1）中，取α＝β＝γ＝1.

例1 考虑问题（1）在区间（-1，1）上，有如下形式的解析解，即

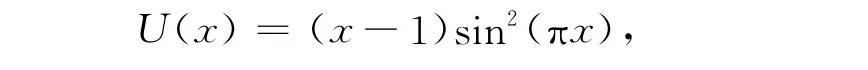
其中：右端项为f（x）＝（x-2）sin2（πx）-［π（x+1）+4π2（x-1）］sin（2πx）-2π2（x-4）cos（2πx）.

在半log尺度下，当h＝1／2时，L2-误差及H1-误差随N的变化情况，如图1（a）所示.从图1（a）可知：随着N的增大，误差（ε）随N呈指数衰减.说明对于光滑解，数值解具有所谓的谱收敛.在log-log尺度下，当N＝10时，L2-误差及H1-误差随h的变化情况，如图1（b）所示.从图1（b）可知：误差关于h呈代数衰减.

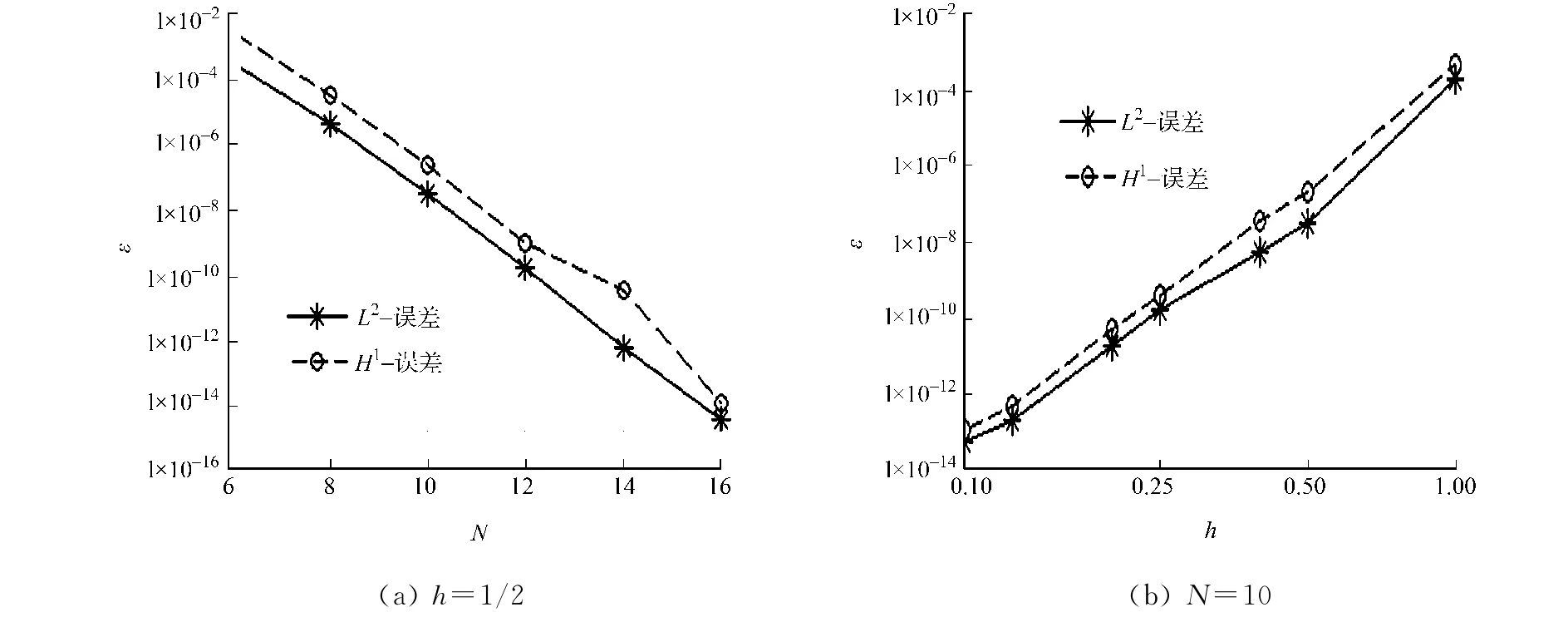
图1 误差的变化Fig.1 Change of the error

3 结束语

用Legendre-Petrov-Galerkin谱元法求解三阶微分方程，将计算区间剖分成一系列的小区间，相应地将问题转化成一系列的子问题.构造恰当的试探函数和检验函数，并对得到稀疏的线性系统再进行求解.数值结果表明：方法是高精度的，将其应用于求解具有高频振荡解的问题也是可行的.

［1］ CANUTO C，HUSSAINI M Y，QUARTERONI A，et al.Spectral methods：Fundamentals in single domains［M］.Berlin：Springer-Verlsg，2006：401-470.

［2］ CANUTO C，HUSSAINI M Y，QUARTERONI A，et al.Spectral methods：Evolution to complex geometries and applications to fluid dynamics［M］.Berlin：Springer-Verlsg，2007：237-357.

［3］ SHEN Jie，TANG Tao.Spectral and high-order methods with applications［M］.Beijing：Science Press of China，2006：183-298.

［4］ KARNIADAKIS G，SHERWIN S J.Spectralhp element methods for computational fluid dynamics［M］.London：Oxford University Press，2005：187-348.

［5］ JOHN W，HILLIARD J E.Free energy of a nonuiform systerm I：Interfacial free energy［J］.J Chem Phys，1958，28（2）：258-267.

［6］ MICHELSON D M，SIVASHINSKY G I.Nonlinear analysis of hydrodynamic instability in laminar flames-II：Numberical experiments［J］.Acta Astronautica，1977，4（11／12）：1207-1221.

［7］ SIVASHINSKY G I.Nonlinear analysis of hydrodynamic instability in laminar flames-I dervation of basic equations［J］.Acta Astronautica，1977，4（11／12）：1177-1206.

［8］ SHEN Ting-ting，XING Kang-zheng，MA He-ping.A legendre petrov-galerkin method for fourth-order differential equations［J］.Computers and Mathematics with Applications，2011，61（1）：8-16.

［9］ ZHUANG Qing-qu.A legendre spectral-element method for the one-dimensional fourth-order equations［J］.Appl Math Comput，2011，218（7）：3587-3595.

［10］ MA He-ping，SUN Wei-wei.A legendre-petrov-galerkin and chebyshev collocation method for third-order differential equations［J］.SIAM Journal on Numberical Analysis，2000，38（5）：1425-1438.

［11］ SHEN Jie.A new dual-petrov-galerkin method for third and higher odd-order differential equations：Application to the KdV equation［J］.SIAM Journal on Numberical Analysis，2004，41（5）：1595-1619.

［12］ ISMAIL M S.Numberical solution of compulex modified korteweg-de vries equation by petrov-galerkin method［J］.Applied Mathematics and Computation，2008，202（2）：520-531.

［13］ SKOGESTED J O，KALISCH H.A boundary value problem for the KdV equation：Comparison of finite-difference and Chebyshev methods［J］.Mathematics and Computers in Simulation，2009，80（1）：151-163.

［14］ 王振华，马和平.三阶微分方程的多区域Legendre-Petrov-Galerkin谱方法［J］.应用数学与计算数学学报，2011，25（1）：11-19.