求解车辆路径问题的改进蚁群算法
2013-10-11王占锋杜海莲安素芳张翠军
王占锋,杜海莲,安素芳,张翠军
(1.石家庄经济学院 信息工程学院,河北 石家庄050031;2.河北师范大学 电子系,河北 石家庄050023)
1959年,Dantzig和Ramser提出车辆路径优化问题 .这是一个经典的NP-hard组合优化问题,采用传统的数学方法求解往往找不到正确的解,而只有解决了车辆路径优化这个难题,现代物流业配送的效率及性能才能得到提高[1].由于车辆路径问题属于NP-hard问题,利用传统的精确算法无法找到正确的配送路径,实际应用中往往采用启发式算法[2-3].蚁群算法是一种新型的启发式蚂蚁群体仿生优化算法,它利用正反馈原理达到算法的最终收敛来搜索最优解,性能较高,其缺点是求解时程序容易较早收敛,停滞[4].遗传算法是一种仿生型优化算法,其优点是全局搜索能力较强,缺点是没有使用系统中的反馈信息.本文将遗传算法和蚁群算法融合,提出一种改进的蚁群算法,求解车辆路径优化问题.
1 数学模型的建立
令配送中心的编码为0,n个需要配送商品的客户的编码依次为1,2,…,n.设编码为i的客户的需要配送的货物量为gi(i=1,2,…,n),设m辆汽车可以完成所有配送任务,qmax为每辆配送汽车的最大载重量;编码分别为i和j的客户之间的运输距离di,j(i=0,1,2,…,n;j=0,1,2,…,n).数学模型的建立需要定义如下3个主要变量[5-7].
1)变量xi,j,k.如果车辆k驶过客户i和j之间的道路,xi,j,k取值为1,否则xi,j,k取值为0;
2)变量yk,i.如果车辆k为编号为i的客户配送任务,yk,i取值为1,否则yk,i取值为0;
3)变量di,j.客户i和客户j之间运输成本定义为行驶时间、运输距离或运输费用等,文中将di,j定义为客户i和j之间的运输距离.
建立的数学模型中,目标函数的作用是使所有汽车的运距(行驶距离)之和z最短,即

同时,建立的约束条件是约束配送汽车的最大载重量,即
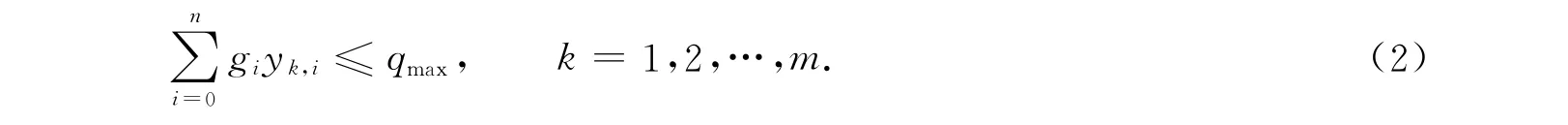
为保证只允许一辆车k完成编号为i的客户的运输任务,即
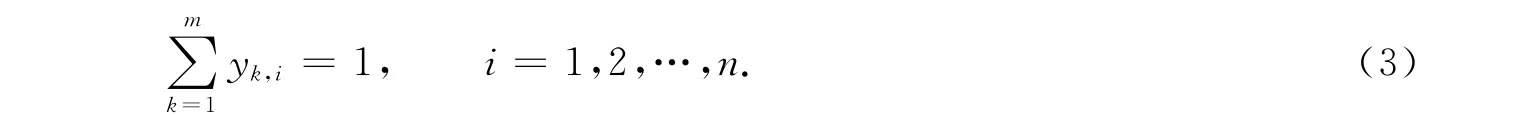
为限制只允许一辆汽车经过某一客户,则有
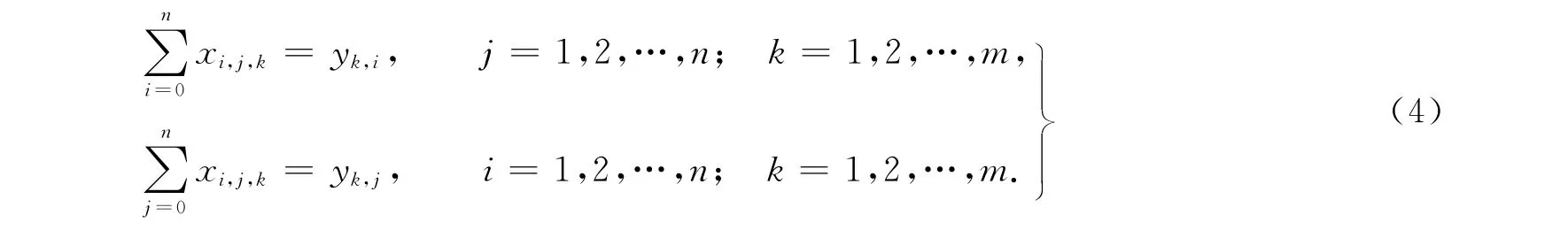
2 应用蚁群算法求解车辆路径
使用蚁群算法求解车辆路径优化问题,需定义如下变量[8-10]:
1)ηi,j为定义为边(i,j)的能见度;2)τi,j(t)为时刻蚂蚁残留在边(i,j)上的信息素;3)Δτi,j(t)为蚁群经过一次迭代后,边(i,j)上的信息素增值;4)Lk为经过一次迭代后,编号k的蚂蚁经过所有的客户点后爬行的路径长度;5)α为启发因子,表示信息素影响蚂蚁选择路径的相对重要性(α≥0);6)β为期望启发因子,表示能见度影响蚂蚁选择路径的相对重要性(β≥0);7)ρ为信息素挥发系数(0≤ρ≤1),1-ρ定义为信息素的残留系数;8)Q为经过一次迭代后,蚂蚁在经过所有客户后,在路径上所释放的信息素总量;9)tabuk为客户禁忌表,表示已完成配送任务的客户所构成的集合;10)allowedk为允许编号k的蚂蚁移动时可以移向的客户所构成的信息表;12)tourk为经过一次迭代后,编号k的蚂蚁所经过的所有客户编号所构成的集合.
文中车辆路径采用自然数编码,即首先计算客户之间、客户与配送中心之间的距离di,j,并初始化每个客户的货物需求量,同时通过计算确定配送货物需要的最少车辆数.蚂蚁从配送中心出发,其选择概率的计算式为
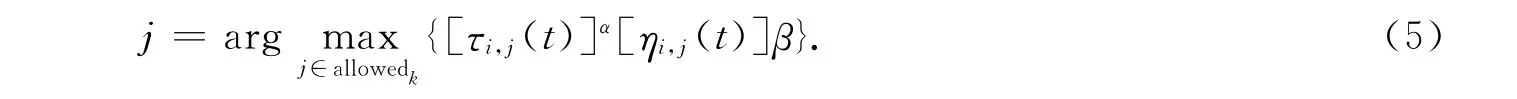
从allowedk中选择下一个配送客户,直到汽车已配送客户的货物量之和超过其最大载重时,汽车驶回配送中心,形成一条子路径,将若干条子路径构成车辆配送问题一个正确解[11-12].
allowedk,τi,j(t),ηi,j(t),α,β等参数前文已经提到,这里i为蚂蚁所在的客户点编号,j表示下一个移动概率最大的客户编号.这种路径选择规则与基本蚁群算法类似,但平衡了信息素和能见度的作用,更接近于实际的蚁群系统.
车辆路径的适应度函数[13-15]定义为

式(6)中:δ为正常数;k为编号k的蚂蚁;z为蚂蚁经过所有客户后爬行的路径长度.
3 应用改进后的遗传变异算子优化路径
改进后的遗传算法是根据概率mp1(0<mp1<1)的大小来执行不同的逆转变异.这样扩大了父个体基因信息的选择来源,从而增大了子个体的多样性,防止算法过早收敛[16-20].
改进后的遗传变异算子有如下2个步骤.
1)随机选择父个体p1上一位基因r1,假设r1=1.
2)随机生成一个实数 ,范围在 (0,1)区间,令r和mp1比较,然后执行以下不同的步骤:如果r≤mp1,从父个体p1中随机选取不同于r1的一个基因作为r2;如果r>mp1,重新选择另外一个父个体p2,从父个体p2中选取r2,令父个体p1中r1和r2之间的编码逆转,产生下一代子个体o1.
将第一阶段得到的局部最优解编码作为父代基因信息,然后使用改进的逆转变异算子,得到下一子代的基因信息,符合条件的车辆配送路径 .从生成的子代中选出目标函数最优者,即得到车辆路径的全局最优解.
4 仿真测试及结果分析
以车辆路径Eil22问题为例,测试算法性能.物流中心使用一些载重为6t的汽车,对21个客户配送货物,物流中心编号为0,客户编号分别为1,2,…,20,21,要求使用车辆最少,行车路线最短.客户坐标及客户的需求量,如表1所示.
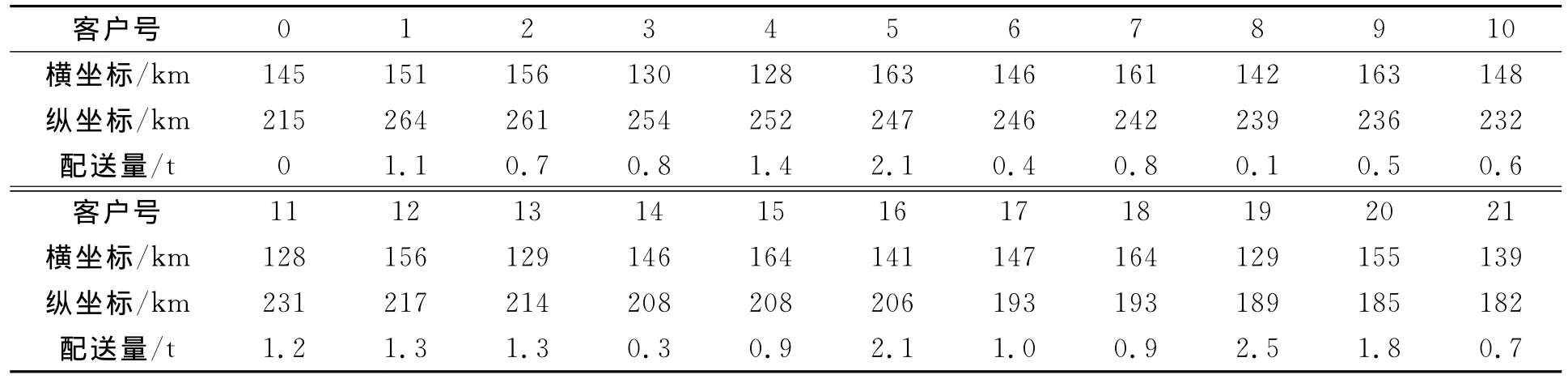
表1 客户坐标及配送量表Tab.1 Coordinates and distribution of customers
改进后蚁群算法求解客户车辆路径测试结果,如表2所示.参数设置:Nc,max=10,α=1,β=3,ρ=0.5,Q=1,Nc,max1=100,P=0.6,m=21(蚂蚁数与客户数相同),逆转变异概率mp1=0.3.算法共运行10次,运行后最优解为0-9-7-5-2-1-6-8-0-14-16-21-19-0-12-15-18-20-17-0-10-3-4-11-13-0,路径长为377.3km.

表2 改进后蚁群算法求解客户车辆路径问题测试结果Tab.2 Test results of customers vehicle routing problem based on improved ant colony algorithm
从表2可知:算法运行一次的平均时间为0.295s,找到最短路径的概率为60%,其他几次找到的配送路径距离与最优解差值很小,与文献[5-6]中的算法相比,算法性能有很大的提高.
另外,分别使用遗传算法和改进后的蚁群算法对文献[4-5]中8个客户的数据进行实验 .其中:配送中心编号为0,8个客户分别编号为1,2,…,8.使用遗传算法求解车辆路径问题的路径中达到最优解(最优解总长度为67.5)的次数占总数的50%,平均路径长度为68.55.
使用改进后的蚁群算法对文献[4-5]中的8客户的配送问题进行仿真实验.参数设置:Nc,max=10,α=1,β=3,ρ=0.5,Q=1,Ncmax1=200,P=0.6,m=8逆转变异概率mp1=0.3.程序运行10次,其中7次找到了最短路径,平均路径长度为68.05.通过实验结果对比,可以看出改进后的蚁群算法要比使用遗传算法求得的最短车辆路径的概率要高,算法性能有明显的提高.
5 结论
文中车辆配送路径采用了客户和配送中心使用自然数编码的方法,并将遗传算法中的逆转变异算子融合到现有的蚁群算法中,对使用蚁群算法求得的最优解进行二次优化,得到配送路径最优解的基因表达式.
仿真实验证明,求解车辆路径优化问题时,使用文中改进后的蚁群算法有如下优点:1)避免了单纯使用遗传算法求解车辆路径优化问题时,选择、交叉、变异等遗传操作的复杂性,程序运行速度较慢,性能较低的现象;2)与现有的求解车辆路径优化问题的蚁群算法相比,具有更快的运行速度,找到最优解的概率更高;3)应用文中所改进的蚁群算法时,操作上切实可行,避免了蚁群算法过早收敛,求解效率和性能都较高.
[1] 潘正君,康立山,陈毓屏.演化计算[M].北京:清华大学出版社,1998.
[2] 段海滨 .蚁群算法原理及其应用[M].北京:科学出版社,2005.
[3] DORIGO M,MANIEZZO V,COLOMI A.The ant system:Optimization by a colony of cooperating agents[J].IEEE Transactions on Systems,Man,and Cybernetics:Part B,1996,26(1):29-41.
[4] 姜大立,杨西龙,杜文,等.车辆路径问题的遗传算法研究[J].系统工程理论与实践,1999,19(6):40-44.
[5] 王占锋,张翠军,许冀伟,等.求解非满载车辆调度问题的改进遗传算法[J].计算机工程与设计,2008,29(15):3991-3993.
[6] WANG Zhan-feng,DU Hai-lian,HU Ji-chao,et al.An improved genetic algorithm for vehicle routing problem of non-full load[C]∥3rd International Symposium on Intelligent Information Technology Application.Washington D C:IEEE Computer Society,2009:173-175.
[7] 樊建华,王秀峰.基于免疫算法的车辆路径优化问题[J].计算机工程与应用,2006,42(4):210-212,217.
[8] 张翠军,刘坤起.求解一般车辆优化调度问题的一种改进遗传算法[J].计算机工程与应用,2004,40(33):207-208,211.
[9] 戴树贵,陈文兰,潘荫荣,等.多配送中心车辆路径安排问题混合蚁群算法[J].四川大学学报:工程科学版,2008,40(6):154-158.
[10] BULLNHEIMER B,HARTL R,STRAUSS C.An improved ant system algorithm for the vehicle routing problem[J].Annals of Operation Research,1999,89(13):319-328.
[11] BRYSY O,DULLAERT W.A fast evolutionary metaheuristic for the vehicle routing problem with time windows[J].International Journal of Artifical Intelligence Tools,2002,12(2):143-157.
[12] 柳林,朱建荣.基于混合蚂蚁算法的物流配送路径优化问题研究[J].计算机工程与应用,2006,42(13):203-205.
[13] GLOVER F.Tabu search:a tutorial[J].Interfaces,1990,20(4):74-94.
[14] 丁建立,陈增强,袁著祉.遗传算法与蚂蚁算法的融合[J].计算机研究与发展,2003,40(9):1351-1356.
[15] 陈陵,沈洁,秦玲,等.基于分布均匀度的自适应蚁群算法[J].软件学报,2003,14(8):1379-1387.
[16] 张翠军,张敬敏,王占锋.基于车辆路径问题的蚁群遗传融合优化算法[J].计算机工程与应用,2008,44(4):233-235.
[17] 刘志硕,申金升,柴跃廷.基于自适应蚁群算法的车辆路径问题研究[J].控制与决策,2005,20(5):562-566.
[18] 唐连生,程文明,张则强,等.基于改进蚁群算法的车辆路径仿真研究[J].计算机仿真,2007,24(4):262-264.
[19] 徐强,宋海洲,田朝薇.解TSP问题的蚁群算法及其收敛性分析[J].华侨大学学报:自然科学版,2011,32(5):587-591.
[20] 杨四海.TSP的等价解及其对免疫遗传算法的干扰[J].华侨大学学报:自然科学版,2007,28(1):27-29.
