变系数5阶Korteweg-de Vries方程的Lax对和自-Bäcklund变换研究

王嘉谋，王尚户，何莉敏

(内蒙古科技大学数理与生物工程学院，内蒙古包头014010)

随着研究领域和研究深度不断扩展，众多科研工作者逐渐发现常系数非线性发展模型并不能刻画众多复杂非线性现象的传播特性，故为描述孤立波在不同介质中的演变特性，人们纷纷提出众多含有变系数的模型，如变系数 Korteweg-de Vries(KdV)方程、变系数 Schrö dinger方程、变系数Kadomtsev-Petviashvili方程、变系数 Gardner方程等.文中则以在很多物理环境中广泛应用的变系数5阶KdV方程为研究对象，其形式如下［1-2］:

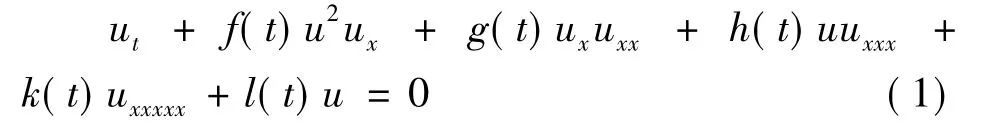
式中:u(x，t)为孤立波的振幅;f(t)，g(t)，h(t)，k(t)和l(t)分别为实解析函数.方程(1)可用于描述量子力学、非线性光学、江河等领域中存在非均匀传输介质孤立子的传播，包括如下特殊情况:

1) 当f(t)= α，g(t)= β，h(t)= γ，k(t)=1和l(t)=0时，方程(1)变为常系数5阶KdV方程:

式中:α，β和γ为任意的非零实常数，而当α =30，β =20和γ =10时，方程(2)为Lax方程［3］;当α =β = γ =5时，方程(2)为Sawada-Kotera方程［4］;当α=β=25和 γ =10时，方程(2)为Kaup-Kupershmidt方程［5］;当 α =2，β =6 和 γ =3时，方程(2)为Ito方程［6］.上述前3个方程都是Lax可积的，故具有无穷守恒律，而由于Ito方程并不是完全可积的，故只有有限的守恒律.

2)当l(t)=0时，方程(1)变为

通过齐次平衡方法和从变系数模型到常系数模型的变换，在文献［2］中已经推出该方程的Lax对、Darboux变换和一系列解析解.

文中首先利用Ablowitz-KaupN-ewell-Segur(AKNS)变换推导出方程(1)的Lax对，进而构造自-Bäcklund变换和一系列的孤子解，最后分析讨论不同变系数函数项对孤立波传播演变特征的影响.

1 变系数5阶KdV方程可积性质

1.1 推导Lax对

根据AKNS系统［7-8］，可假设方程(1)具有如下形式的Lax对，即其线性本征值问题为

式中:

式中:φ =(φ1，φ2)T为实列向量;λ 为与x和t无关的谱参数;h(t)，l(t)，A(x，t，λ)，B(x，t，λ)和 C(x，t，λ)为需确定的解析函数，进而通过相容性条件

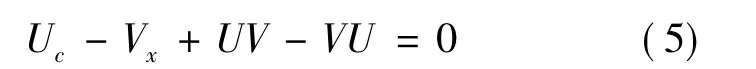
可确定各待定函数并推出方程(1).

为确定方程(1)的Lax对，可将函数A(x，t，λ)，B(x，t，λ)和 C(x，t，λ)按如下形式展开

式中:ai(x，t)，bi(x，t)和 ci(x，t)为解析函数.将上述各函数带入相容性条件式(5)中，并分别取谱参数各幂次的系数为零，可得

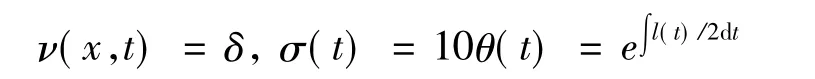
约束条件为

而

式中:δ为任意实常数，进而由λ的零次幂可推得

而上式即为方程(1)在约束条件(6)下的简化形式，并具有较好的可积性质，如Lax对、Bäcklund变换、非线性叠加公式和孤子解等.

1.2 Bäcklund变换

作为一种行之有效的方法，人们可通过构造Bäcklund变换构造出众多的非线性偏微分方程的孤子解，Bäcklund变换主要包括两种不同的形式:两个不同方程解之间的联系和同一个方程两个不同解之间的关系［9］.

为推出方程(7)的自-Bäcklund变换，可设θ=φ1/φ2，故方程(4)变为

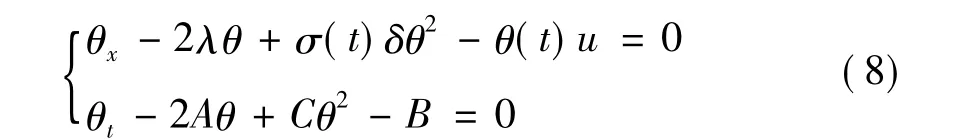
并可以证明式(8)在如下变换下具有不变性:

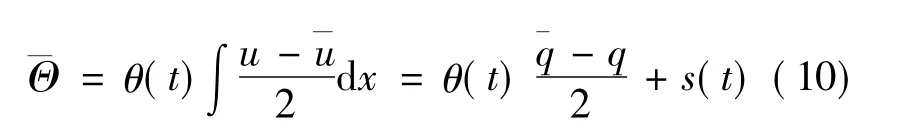
式中:u= － qx= －，而 s(t)为积分函数.将式(10)代入式(8)中的第1式，可得方程(7)自 -Bäcklund变换中的x部分，

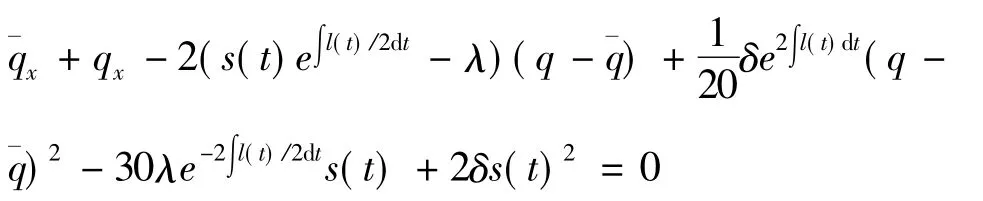
将式(10)代入式(8)中的第2式，经过一系列的处理和运算，可得方程(7)自-Bäcklund变换中的t部分，

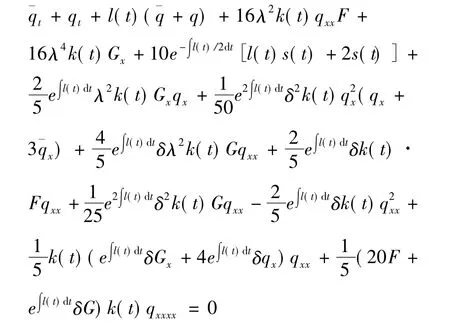
式中:F=e∫l(t)/2dtδs(t)－ λ，G=－q.

为了简单，可取 s(t)= λe－∫l(t)/2dt/δ和 δ=20/ε，方程(7)的自 －Bäcklund变换可简化为

2 方程(1)孤子解

一般地，利用自-Bäcklund变换(11)，可由方程(7)的一个已知解推导新的解析解.若取¯u为方程(7)的平凡解，并代入到自-Bäcklund变换(11)中，可得

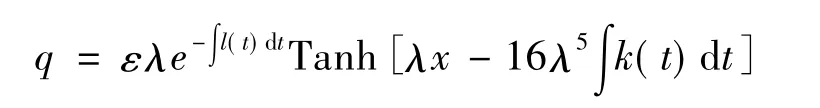
进而可推出5阶KdV方程(7)的单孤子型解

式中: － ελ2e－∫l(t)dt和1/λ 代表孤立波的振幅和波宽.

为刻画孤子解在实际物理环境下的传播形态，需结合物理背景参数，对式(12)中的参数进行适当选取.

当 ε = －1，λ =0.5，k(t)=1和l(t)=0时，方程(7)具有行波解，其波形和速度在传播过程中可保持不变，具有很好的孤子特性(图1).

图1 方程(7)行波解的传播演变特征Fig.1 Solution of equation(7)is travelling-wave case with the parameters as shown in the paper

当 ε = －2，λ =0.5，k(t)= －2sin(2t)和l(t)=0时，方程(7)具有非行波解，其速度在传播过程中随时间不断发生周期性变化，但孤波的振幅可保持稳定不变，如图2a).而当 ε =－2，λ =0.5，k(t)=0和l(t)=sin(2t)时，方程(7)则具有振幅不断变化的非行波解，即不断周期性变化，而传播速度却可保持稳定不变，如图2b).当 ε =－ 2，λ =0.5，k(t)=－ 2sin(3t)和 l(t)=1.5sin(t)时，方程(7)则具有振幅和速度随时间不断变化的非行波解(图3).

图2 方程(7)随时间不断变化的非行波解的传播特征Fig.2 Solitonic solution of equation(7)is beyond the travelling wave

图3 方程(7)随振幅和速度时间不断变化的非行波解Fig.3 Non-travelling wave solution of equation(7)shows that the amplitude and velocity of the wave is periodically variable with the evolution of time

3 结论

文中以含有变系数函数的5阶KdV方程为研究对象，首先利用AKNS系统推出该方程存在孤子解得约束条件和Lax对，进而构造出方程的自-Bäcklund变换和一系列孤子解，并给出了变系数函数项对孤子传播特征的影响，通过分析讨论可知方程(7)在一定的约束条件下具有丰富的孤子解.基于本文获得的变系数5阶KdV方程的Lax对，可进一步构造方程的非线性叠加公式、Darboux变换、多孤子解、无穷守恒律等可积性质，为描述复杂孤波的传播特性奠定较好的基础.

References)

［1］Güdtas ü，Hereman W.Symbolic computation of conserved densities for systems of nonlinear evolution equations［J］.J Symb Comput，1997，24:591-621.

［2］Chen B，Xie Y C.An auto-Bäcklund transformation and exact solutions of stochastic Wick-type Sawada-Kotera equations［J］.Chaos，Solitons and Fractals，2005，23:243-248.

［3］Las P D.Integrals of nonlinear equations of evolution and solitary waves［J］.Commun Pur Appl Math，1968，21:467-490.

［4］Sawads K，Kotera T.A method for finding N-soliton solutions of the KdV equation and KdV-like equation［J］.Prog Theor Phys，1974，51:1355-1362.

［5］Kupershmidt B A.A super Korteweg-de Vries equation:an integrable system［J］.Phys Lett A，1984，102:213-215.

［6］Ito M.An extension of nonlinear evolution equations of the K-dV(mK-dV)type to higher orders［J］.J Phys Soc Jpn，1980，49:771-778.

［7］Ablowitz M J，Kaup D J，Newell A C，et al.Nonlinear evolution equations of physical significance［J］.Phys Rev Lett，1973，31:125-127.

［8］Ablowitz M J，Kaup D J，Newell A C，et al.The inverse scattering transform-Fourier analysis for nonlinear problems［J］.Stud Appl Math，1974，53:249-315.

［9］Konno K，Wadsti M.Simple derivation of Bäcklund transformation from riccati form of inverse method ［J］.Prog Theor Phys，1975，53:652-1656.