星载激光测高仪辅助卫星摄影测量浅析

岳春宇 郑永超 陶宇亮

（北京空间机电研究所，北京100076）

1 引言

卫星摄影测量立体测绘，是通过地面控制点和卫星遥感影像中的同名关系进行空中三角测量，获取地面的三维信息。利用辅助信息尽量减少地面控制点是卫星摄影测量的发展趋势。激光测高仪是一种能够精确获得地面三维信息的主动遥感手段，可以有效弥补 CCD传感器反隐身能力、目标定位能力和三维探测能力等不足。使用激光测高仪辅助空中三角测量立体测图，把激光距离观测值解算得到的地面高程信息作为控制元素，可以参与影像平差计算，提高数字地面模型精度。另外，当激光测高获得的高程点精度足够高时，可以为测绘成图提供地面控制，为后续的全球观测提供基础和保障。

空中三角测量由地面控制点坐标根据摄影光线关系求解影像内外方位元素，再由影像方位元素和影像中的同名关系，交会计算得到地面点坐标，从而获得地物空间信息。采用卫星立体影像进行空中三角测量平差测图对于影像的定位精度有较高要求。一般通过地面控制点来对卫星进行在轨检校，标定卫星成像时的内外方位元素，在影像的重叠区内寻找同名点，根据卫星成像几何模型计算地面点的三维信息。

实际立体测绘空三计算中，有如下问题需要解决：

1）部分地区控制点布设困难。在进行空三计算时，西部无人区及国外很多地区无法布设地面控制点。

2）部分地区同名点获取困难。对于纹理重复及匮乏地区很难自动获取同名信息，在这些区域通过交会计算无法得到高精度的高程信息。

3）植被覆盖等遮掩、以及阴影导致无法获取地面信息。如部分地区在有森林等植被覆盖时无法通过交会计算获得地表高程。

对于上述问题，激光测高仪获取的测高数据与立体测绘相机获取的影像数据相结合可以很好地解决。

1）激光测高仪可以获得较高精度的地表高程信息，当通过检校使激光测高数据平面精度达到一定要求时，可以作为地面控制点，避免了人工野外布设控制点的工作，减少作业成本，同时可以获得大量国外地区的地面控制。

表1 高程控制点布设比较Tab.1 Comparison of elevation control point layouts

2）激光测高仪不需要获取同名信息，直接根据测得的卫星到地面点的距离及卫星的位置和飞行姿态计算得到该点高程信息。

3）激光具有穿透植被冠层的能力，根据激光回波数据可以获得地表距离数据和非地表距离数据，根据回波波形分析，去掉非地表数据既可以获得被遮挡的地表的高程信息。

2 星载激光测高仪辅助卫星摄影测量方案

传统的摄影测量光束法区域网平差立体测图的地面控制方案需要在平差区域的四角布设4个平面高程控制点，且同时在区域两端布设两排高程控制点，如图1所示[1]。其中三角表示平面高程控制点，圆点表示高程控制点。

图1 空三立体测图地面控制示意图Fig.1 Control points in aerotriangulation

文献[2]采用四角点布设地面控制点对4幅北美港口丘陵地区IKONOS影像进行立体测图实验，平面和高程精度分别为0.440m和0.939m，满足1︰10 000成图精度要求。而进一步实验中，增加控制点数对成图精度提高改善不明显。从而得出了4个角点布设地面控制点即可满足实际应用的结论，对我国卫星影像空三测图具有重要参考意义。据文献[3]报道，在我国第一颗高精度民用测绘卫星“资源三号”发射后，采用平面精度 1m，高程精度2m的高精度参考影像对其影像进行标定。空三平差结果平面精度为4m，高程精度为2m，满足1︰50 000测图需求。而文献[4]则利用4个精度优于0.1m的GPS地面点作为控制点，另外14个GPS点作为检查点，对“资源三号”卫星影像进行空三测图，得到的平面精度为2.93m，高程精度为2.07m。

上述成果表明，目前对于高分辨率遥感卫星影像，只需要少数高精度控制点或采用较高精度的参考影像或检校场，即可获得满足需要的观测定位精度。在实际应用中，可以在立体测绘相机两测安置激光测高仪，以一定频率对地发射光束，即可获得较高精度分布在影像两端的高程点。或者安装多波束激光测高仪，在相机成像区域获得均匀分布的高程点。图2为两种激光测高仪辅助测绘方案示意图，黑圆圈表示激光测高仪光斑足印。

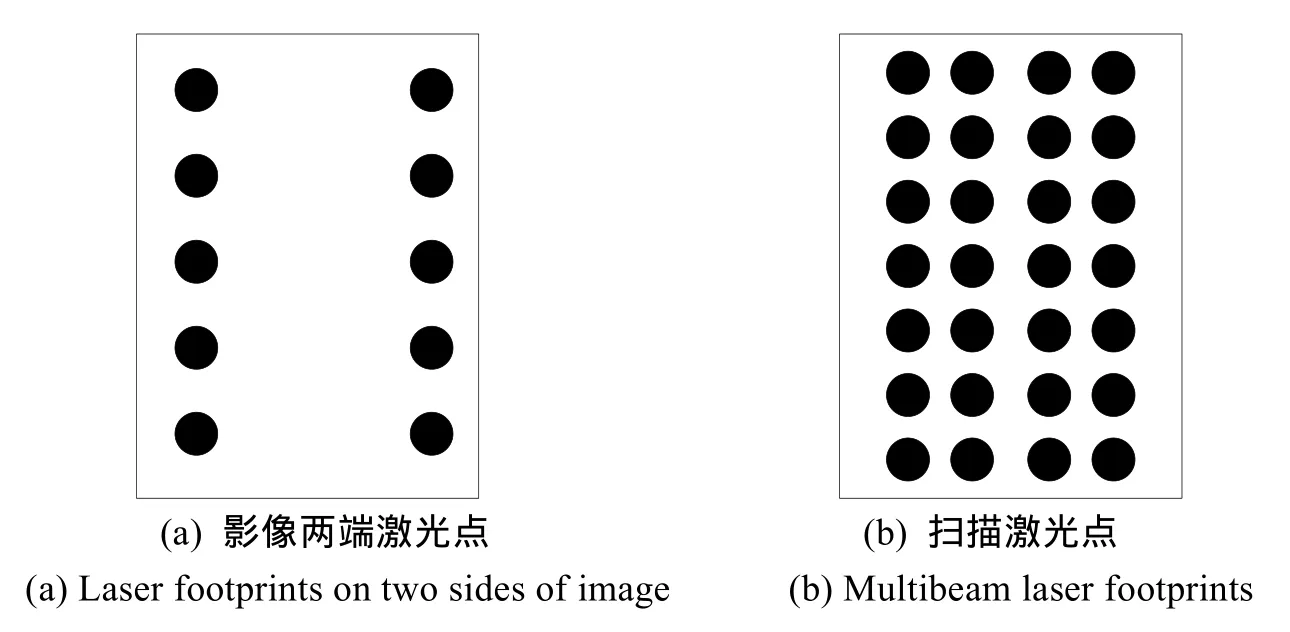
图 2 星载激光测高仪辅助测绘方案激光点分布示意图Fig.2 Laser footprints of space-borne laser altimeter supported aerotriangulation

星载激光测高仪高程精度可达分米级，而水平精度相对较低。如唯一在轨对地观测的星载激光测高系统GLAS，高程精度为0.15m，平面精度为几十米[5]。但是激光测高仪与测绘相机相比，外方位角元素对高程坐标的误差传播系数仅为其几十分之一[6]。通过激光测高数据与参考DEM匹配，或地面布设角反射器标定激光足印位置，改善激光测高仪的水平精度，在相同辅助定向参数情况下，激光测高观测可显著改善对地观测的高程精度，作为地面控制点参与空三平差计算。

卫星影像摄影测量观测方程为

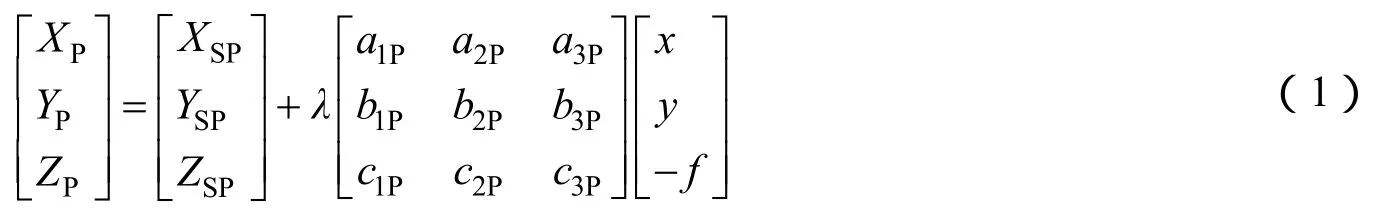
激光测高仪对地观测方程为

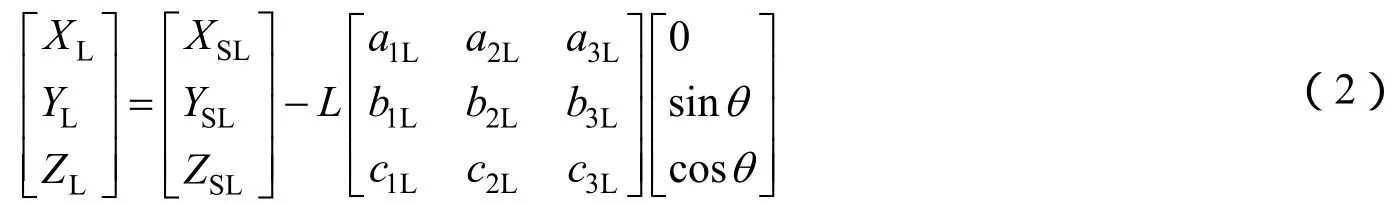
把测绘相机与激光测高仪的方位元素和两种观测方法获得的地面坐标作为观测值引入到联合平差模型，在无控制点且外方位元素视为观测值时，星载激光测高仪辅助空中三角测量光束法平差误差方程为

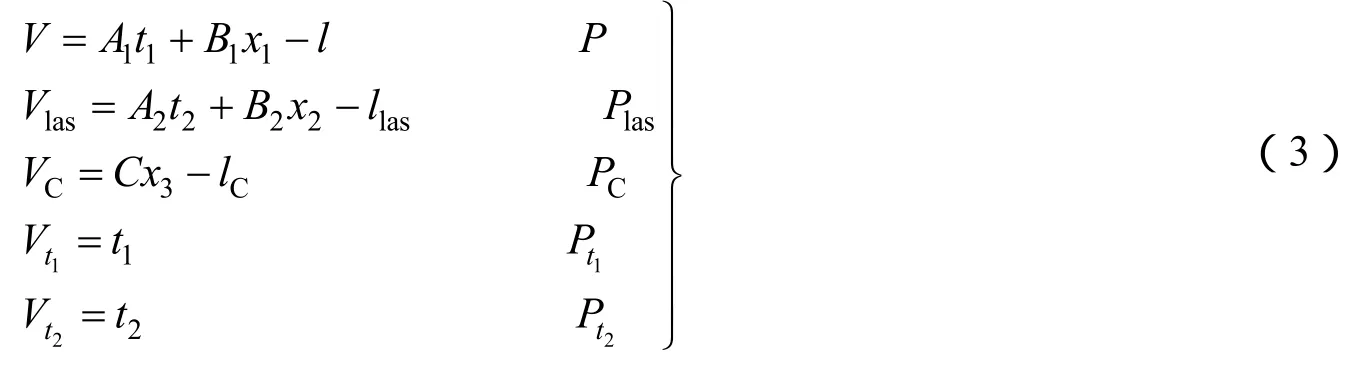
式中 第一个方程是立体相机影像像点坐标误差方程；第二个方程是激光测高仪投影坐标误差方程；第三个方程是立体相机和激光测高仪外方位元素之间关系的观测误差方程；第四个方程是立体相机外方位元素观测误差方程；第五个方程是激光测高仪外方位元素观测误差方程；为各方程观测值改正数向量；t1、t2分别为相机和激光测高仪外方位元素向量；x1、x2分别为相机和激光测高仪对地观测坐标值向量；x3为立体相机和激光测高仪外方位元素之间关系的观测向量；C为系数矩阵；l、lasl、Cl分别为第一、第二和第三个方程的观测值残差；分别为各误差方程观测值的权。联合平差时一般根据各观测值的方差定权，初始权值为方差的倒数，各方程中观测值的方差由仪器标称及先验知识获得。

卫星搭载的激光测高仪可以在立体测绘相机成像时同步获得均匀分布的大量精度较高的高程控制点，避免了部分地区布设控制点困难的问题。激光测高数据和影像数据同时获取，辅助定向参数相同，经过系统偏差检校即可快速配准实现三维量测[6]。在有地面控制测图时，高程控制点可以作为高程多余观测，提高平差精度和稳定性；在无控制点或缺少控制点的情况下，则可以直接作为控制点，进行无地面控制测图。

3 星载激光测高仪辅助卫星摄影测量精度分析

3.1 理论精度分析

图3为激光测高仪对地观测原理图[6]。S为激光测高仪的空间位置，P为所观测的地面点，L为距离测量值，θ为激光测高仪指向角，(φ, ω, κ)为激光测高仪外方位角元素。

图3 激光高仪几何定位原理Fig.3 Geometric positioning of space-borne laser altimeter

若(X, Y, Z)为观测得到的地面坐标，(XS, YS, ZS)为激光测高仪的外方位元素。由于激光测高仪观测方程是非线性的。为了便于计算，同时对引起测高误差的因素进行分析，对激光测高观测方程式（2）用泰勒公式展开成线性形式。

假定距离测量值与轨道高度相等，为500km，L=500km，φ = ω = κ ≈ 0，激光测高仪指向星下点，即θ=0。则式（4）中地面坐标( X, Y, Z )的精度为：

激光测高仪的外方位元素为卫星平台辅助定向参数，与立体测绘相机一致。当今高分辨率遥感卫星外方位线元素测定精度可达到分米级，对定位精度影响较小[7]，外方位角元素测定精度达到1″以上。仅以平坦地区为例，参考GLAS系统的误差补偿方法[8]，假设激光测高仪指向角误差为1″，激光测距误差为 0.3m，其中包括大气延迟、固体潮、以及光斑大小等对测距影响的补偿。则 ΔXS=ΔYS=ΔZS=0.1m，Δφ=Δω=Δκ=Δθ=1″，ΔL=0.3m。此时计算得到 δX=2.43m, δY=2.43m, δZ=0.32m。当卫星影像地面分辨率为5m以上时，激光测高仪水平误差在一个像素内，可以忽略。

3.2 仿真实验分析

采用某真实卫星影像，加入仿真激光测高数据，使用测绘相机与激光测高仪的方位元素和两种观测方法获得的地面坐标作为观测值引入联合平差，根据式（3）进行解算，验证星载激光测高仪辅助卫星摄影测量立体测绘的定位精度。仿真数据原始定位精度见表2第一栏，激光测高观测精度假设与3.1中一致，为δX=2.43m, δY=2.43m, δZ=0.32m。由于目前星载激光测高仪工作频率较低，无法在观测区域大量获取测高值，实验中只在平差区域四角生成激光测高仪观测值。实验结果见表2第二栏激光观测参与平差精度。

表2 实验结果Tab.2 Experiment results m

由表2可以看出，在3.1假设的理想状态下，当激光测高数据参与立体影像空三平差后，地面定位精度有了显著提高。

经上述分析可知，激光测高仪的高程观测精度在理想条件下主要与其测距精度有关，所以可以有效地提高高程观测精度。激光测高仪的平面精度中沿轨方向精度优于垂直于轨道方向的精度，受外方位角元素的影响较大，经过与参考 DEM匹配或地面标定后则可以有效提高平面精度，直接作为控制点参与测图平差计算。

4 结束语

本文论述了星载激光测高仪辅助卫星摄影测量立体测绘的原理和意义。根据实际生产实验中的经验和原则，给出了星载激光测高仪辅助空中三角测量立体测绘方案，对星载激光测高仪的观测定位精度进行了分析,并进行了星载激光测高仪辅助空中三角测量仿真实验。分析结果表明，星载激光测高仪的高程精度主要与测高仪测距精度相关，相对于立体测绘相机，受其他因素影响较小。而激光测高仪测距精度较高，所以激光测高仪辅助空中三角测量立体测图能够提供大量高精度高程观测值，参与平差计算，有效地提高成图精度。但是激光测高仪的平面精度，主要是垂直轨道方向的精度受轨道平台影响较大，尤其是外方位角元素的定姿精度。另外地形起伏以及激光足印光斑对激光测高仪的水平精度也有较大影响，后续的研究可以从卫星地面检校或者激光脚点定位来改进测高仪平面精度，从而提高星载激光测高仪的地面观测精度，进而实现无控测图及全球观测。

References)

[1]袁修孝，朱武，武军郦，等. 无地面控制GPS辅助光束法区域网平差[J]. 武汉大学学报（信息科学版），2004, 29(10):852-857.YUAN Xiuxiao, ZHU Wu, WU Junli, et al. GPS-supported Bundle Block Adjustment Without Ground Control Points[J].Geomatics and Information Science of Wuhan University, 2004, 29(10): 852-857.(in Chinese)

[2]张过，李德仁，袁修孝，等. 卫星遥感影像的区域网平差成图精度[J]. 测绘科学技术学报，2006, 23(4): 239-241.ZHANG Guo, LI Deren, YUAN Xiuxiao, et al. The Mapping Accuracy of Satellite Imagery Block Adjustment[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(4): 239-241. (in Chinese)

[3]李德仁，王密. “资源三号”卫星在轨几何定标及精度评估[J]. 航天返回与遥感，2012，33(3): 1-6.LI Deren, WANG M i. On-orbit Geometric Calibration and Accuracy Assenssment of ZY-3[J]. Spacecraft Recovery & Remete Sensing, 2012, 33(3): 1-6.(in Chinese)

[4]唐新明. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报，2012，41（2）:191-198.TANG Xinming. Triple Linear-array Imaging Geometry Model of ZY-3 Mapping Satellite and Its Validation[J]. Acta Geodaeticaet Cartographica Sinica, 2012, 41(2): 191-198. (in Chinese)

[5]Sungkoo Bae，Charles Web，Bob Schutz. GLAS PAD Calibration Using Laser Reference Sensor Data[C]. In AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Providence, RI, USA, 2004: 1-10.

[6]余俊鹏，孙世君. 卫星摄影测量观测技术发展的若干思路[C]. 第二十三届全国空间探测学术交流会，厦门，2010：1-6.YU Junpeng, SUN Shijun. Some Strategies about Satellite Photogrammetry[C]. The 23rdNational conference on space explorer, Xiamen, 2010: 1-6.(in Chinese)

[7]余俊鹏，孙世君，毛建杰. 卫星遥感影像外方位元素的误差传播研究[J]. 航天返回与遥感，2011, 32(1): 18-23.YU Junpeng, SUN Shijun, MAO Jianjie. Study on Error Propagation of Exterior Orientation Elements of Satellite Remote Sensing Imagery[J]. Spacecraft Recovery & Remete Sensing, 2011, 32(1): 18-23. (in Chinese)

[8]范春波，李建成，王丹，等. ICESAT/GLAS激光脚点定位及误差分析[J]. 大地测量与地球动力学, 2007, 27(1):104-106.FAN Chunbo, LI Jiancheng, WANG Dan, et al. ICEsat/GLAS Laser Footprint Geolocation and Error Analysis[J]. Journal of Geodesy and Geodynam ic, 2007, 27(1): 104-106. (in Chinese)