某型教练机机载天线与雷达罩的射线入射角的计算

张超超

（中航工业洪都，江西南昌330024）

0 引言

雷达罩是电磁波的窗口，其作用是保护天线，防止环境对雷达天线工作状态的影响和干扰，从而减少驱动天线运转的功率，提高其工作可靠性，保证雷达天线全天候工作。雷达罩的存在，延长了天线的使用寿命，简化了天线的结构，减轻了结构的重量。雷达罩作为雷达系统的重要组成部分，其性能好坏直接影响到雷达系统的能。可以说，雷达罩与天线同等重要。要求雷达罩对天线的电磁辐射特性的影响最小，并且满足战术技术指标的要求。雷达罩技术综合了材料、工艺、机械、电磁、空气动力学和结构力学等学科的知识，设计和制造难度较大。由于雷达罩工作在一种复杂的特殊环境中，对材料的要求十分苛刻，主要使用玻璃纤维复合材料。国外出现了抵御反辐射导弹袭击的防弹天线罩，能抗高速破片和冲击波的打击。

由于空基天线罩是空基电子系统不可缺少的组成部分，其电磁特性的优劣与系统的整体性能密切相关，长期以来，带罩天线的特性分析和天线罩的结构设计一直受到人们广泛的关注。解析法(AM)以几何光学(GO)为基础，通过射线对罩壁入射角的加权平均等效来计算各站位点的罩壁厚度，方法简便有效，并适用于非均匀壁厚天线罩的设计，是一种工程中普遍采用的设计方法。

本文主要运用投影、向量、曲线拟合等数学思想，通过MATLAB工具计算分析机载天线的入射角大小，与雷达罩的标准指标进行比较，确定雷达罩的电性能是否最佳。并应用于某型教练机XXX火控雷达罩。

1 问题来源描述

某型教练机火控雷达罩如图1所示，其雷达罩表面点的三维坐标见图2。

图1 某型教练机火控雷达罩

图2 原始数据点的三维空间分布

将椭圆处放大，我们可以清晰地看到4种颜色的点，即为4个数据文件在空间中的表示，如图3所示。

现需要求得初始点（即为机载天线上的点）到所给数据点的连线与所给数据点所在切面的法线所成的夹角，要求对于所给范围内任意的初始点，每个数据点对应的角度小于70°。但是切面无法求得，故而把问题转化为求初始点到所给数据点的连线与所给数据点所在拟合曲线的切线的法线所成的夹角,如图4所示。

图3 椭圆处放大图

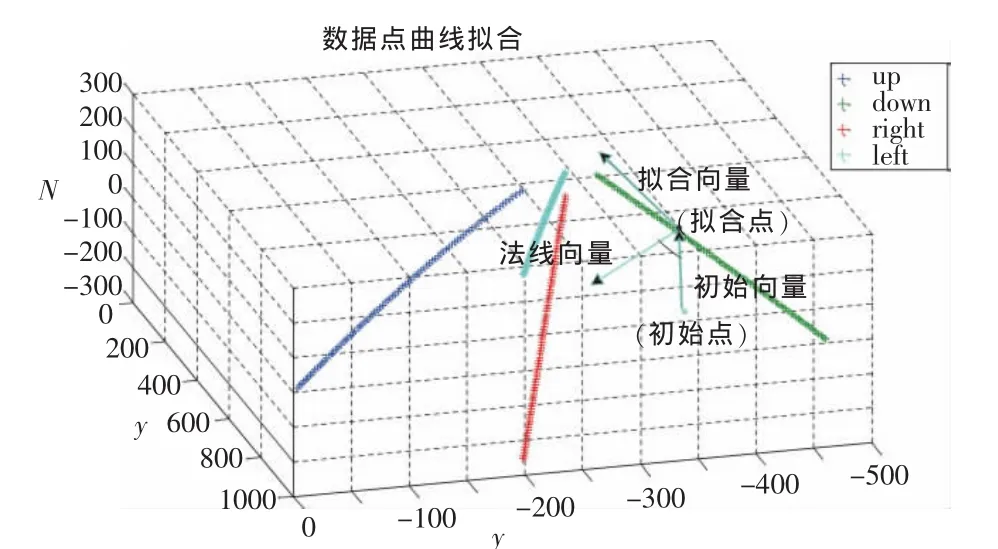
图4 所求夹角示意图

2 问题详细解决方案

2.1 数学思想

2.1.1 二维空间的曲线拟合

曲线拟合(curve fitting)（见图5）是指选择适当的曲线类型来拟合观测数据，并用拟合的曲线方程分析两变量间的关系，用解析表达式逼近离散数据的一种方法。

图5 二维曲线拟合

在科学实验或社会活动中，通过实验或观测得到量x与y的一组数据对(xi,yi)(i=1,2,…,m)，其中各xi是彼此不同的。人们希望用一类与数据的背景材料规律相适应的解析表达式，y=f(x,c)来反映量x和y之间的依赖关系，即在一定意义下“最佳”地逼近或拟合已知数据。f(x,c)常称作拟合模型，式中c=(c1,c2,…cn)是一些待定参数。当c在f中线性出现时，称为线性模型，否则称为非线性模型。

最小二乘法是曲线拟合的核心算法，是一种数学优化技术，它通过最小化误差的平方和找到一组数据的最佳函数匹配。很多其他的优化问题也可通过最小化能量或最大化熵用最小二乘形式表达。

比如从最简单的一次函数y=kx+b讲起，已知坐标轴上有些点(1.1,2.0),(2.1,3.2),(3,4.0),(4,6),(5.1,6.0),求经过这些点的图像的一次函数关系式。当然这条直线不可能经过每一个点，我们只要做到5个点到这条直线的距离的平方和最小即可，这就需要用到最小二乘法的思想。

2.1.2 空间曲线投影

空间曲线投影就是通过空间曲线每一点向坐标作垂线，这个垂线与坐标面的交点集合就是投影，投影是一条曲线，如果想投影到xy平面，只需令。

一个简单的例子：空间直线方程：x=y=z，投影到xy和xz平面后，如图6所示。

图6 在xy、xz平面的投影

2.2 设计解决方法

2.2.1 角度求解方法

众所周知，要求得两条线段之间的角度，有很多种方法，最简单的比如：用量角器、三角形的余弦公式。显然用量角器的方法过于笨重和简单，余弦公式过于复杂，在这里都不方便。这是抽象的数据，而且需要批量式的得到入射角，所以需要用到工程化编程的思想，把问题细化、简单化，把这个问题转化为求两条线段之间夹角。

为了使得到的结果更加高效、快速、简便，在这里运用数组的思想，把三维数据点坐标放到一个数组中，即一个向量，通过求解两个向量之间的夹角（见图7）来得到所需结果。

求得，即

在MATLAB中可通过内置的函数dot，norm，

求得α角。

图7 两向量之间的夹角示意图

2.2.2 三维空间的拟合曲线

二维空间的拟合曲线方程在MATLAB上可以通过polyfit，polyval命令得到，但是没有关于三维空间拟合曲线的求解函数。运用投影的思想，我们先将三维空间曲线投影到xy平面，得到xy平面的拟合曲线方程，有了拟合曲线方程，通过求导法，就能得到关于xy平面在拟合点的切线斜率，同理，再将三维空间曲线投影到xz平面，得到关于xz平面在拟合点的切线斜率，由此可得，关于空间曲线在拟合点的切线向量为

有了拟合曲线方程，就可以通过原始数据的x坐标，求出拟合点的坐标，然后得到初始点到拟合点的向量vectorinitial，我们称之为初始向量。

曲线拟合后，“问题来源描述”一节中的椭圆处放大见图8。

图8 曲线拟合后，椭圆处放大图

2.3 最终计算结果及分析

通过向量求角公式，可以得到初始向量与切线向量的夹角α，但是我们需要的最终计算结果是初始向量与切线的法线做成的夹角vectorα，所以还需要做一个判断，如果α＜90°，则vectorα=90°｜α，如果α＞90°，则vectorα=α｜90°。

最终角度结果趋势见图9。

图9 最终角度结果趋势图

由图可知，雷达罩长度60之后，4条数据线都超过了70°，故此雷达罩没达到要求。整个计算过程所需时间如图10所示，t_end=8.3118s。

图10 最终计算时间

2.4 误差分析

因为初始点与拟合点的差异，误差必然是存在的。经初步分析，如果初始点与拟合点距离越大，数据点所覆盖的雷达罩跨度越短，允许的角度上限α越小， 那么误差越大。令k=1，则误差在允许范围内。 误差分析见图11。

图11 误差分析图

3 结语

对型号雷达罩进行初始数据录入后，再对机载天线与雷达罩的射线入射角进行计算分析。该方法具有普遍性，几乎对所有型号教练机的雷达罩都能适用；而且还具有快速性，对于大量的成批数据，从数据导入，图形、误差分析，到最终结果一目了然只需短短8.3秒就能完成；同时还具有实用性，雷达罩价格昂贵，将该方法应用于检测性能环节上，可以有效判断其性能是否符合指标，减少废品率，从而节约成本，有效控制了机载雷达罩的选择，保证了飞机质量。以后还可以作进一步的改进，如提供友好的人机交互界面、完整的数据输入和图形显示，以方便用户的使用，提高工作效率；或者通过后台编程，把此功能直接嵌入到CATIA中，让用户在使用CATIA分析飞机雷达参数时直接得到所需结果；使误差分析更准确或者将误差降至更低。

[1]万国宾，赵惠玲.机载天线与天线罩的设计与电磁特性分析.制造业自动化，2009.

[2]陈杰.MATLAB宝典,2007.1.