小干扰稳定分析中特定模式降阶法的快速实现

刘 畅，崔 惟，王克文

（郑州大学 电气工程学院，河南 郑州 450001）

0 引言

在电力系统小干扰稳定分析中，特征值分析法[1]是得到广泛应用的有效方法之一。通过求解系统状态矩阵的特征值、特征向量，不仅可直接判断系统的稳定性，还能得到更多的系统信息，为稳定器设置提供指导[1-4]。

求解全维特征值的QR算法具有鲁棒性强、收敛速度快等优点，但矩阵阶数较高时，结果可能存在较大误差。因此，多种部分特征值方法[5-10]相继提出。子空间迭代法[5-6]计算模数较大的一组特征值及特征向量，包括同时迭代法和 Arnoldi法[6]；而降阶选择模式法[7-10]则是将系统矩阵降阶处理，使得降阶系统的特征值包含原系统的主导特征值，以较小计算量得到所需的特征子集，如AESOPS法[7]、选择模态分析法[8-9]等。

概率特征值分析法可以考虑更多的系统运行方式，并得到特征值的统计特性。为了和概率特征值分析法[11]配合使用，文献[12]描述了特定模式降阶法。其大体计算思路与选择模态法[9]类似，由于采用了改进Rayleigh商逆迭代的完整表达，可以直接得到较准确的特征值和特征向量，而迭代初值的确定仍基于全系统状态矩阵的QR计算。文献[13]进而考核了降阶系统下特征值灵敏度的计算误差。文献[12]主要在算法方面实现了降阶系统特征值、特征向量的准确计算，计算效率方面考虑不多。

本文进一步完善特定模式降阶分析法，提高该方法计算振荡模式特征值的效率，通过研究降阶过程，从共享保留机组集、迭代算式调整以及并行计算等方面改进，并用70机和105机算例进行验证。

1 特定模式降阶法

小干扰稳定分析中重点关注的是机电振荡模式或阻尼不足的模式。省级电网状态矩阵的计算规模是几千阶，用QR算法计算包括机电模式在内的全维特征值、特征向量，作为准确计算的初值。

计算第k个特定模式λk时，将状态空间方程中的变量分为两部分：

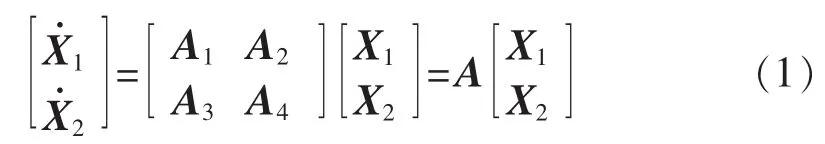
其中，X1为与模式λk强相关机组的状态列向量，X2为待消去的状态列向量，A1、A2、A3、A4为状态矩阵的分块子矩阵。

由式（1）消去 X2，得：

其中，I为单位矩阵，p为微分算子。

通过 B（p）将式（2）简记为：

文献[9]证明了当p=λk时降阶系统的2个重要性质：λk同时为原系统和降阶系统的特征值；若降阶前、后λk的右特征向量分别为Uk0和Ukr，则Ukr等于Uk0中对应X1的元素。因此，降阶系统不会畸变原系统的振荡模式特征值及特征向量相应元素[9]。因此，当 p=λk时，有：

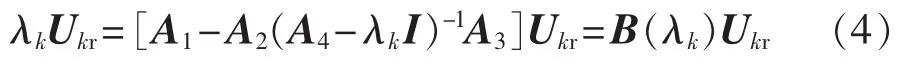
显然 B（λk）是 λk的函数，所以由 B（λk）只能准确计算特定模式λk，其余特征值存在不同程度的偏差。

振荡模式的特征值 λk是复数，B（λk）也是复矩阵。为简化表达，记降阶矩阵如式（5）所示，并略去特征值的下标k。此外，下文中V和U均对应于降阶后矩阵的左、右特征向量。

文献[12]采用三重迭代格式，主要迭代算式如式（6）—（8）所示。

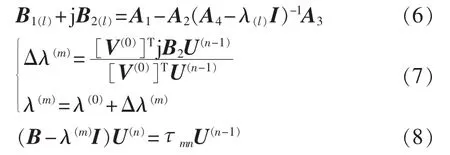
其中，l、m和n分别为外层、次外层和内层的迭代次数，λ（l）为特定模式特征值， τmn为归一化系数。

外层迭代中，先按式（6）计算降阶矩阵，然后用QR 法求解实部 B1（l），得到对应 λ（l）的特征值 λ（0）和左、右特征向量 V（n-1）、U（n-1）。

而次外层迭代中，将虚部 jB2（l）作为B的复数形式的变化量，按式（7）计算特征值修正量。其中，初始值 V（0）的采用保证了算式的完整表达[12]。

内层迭代，按式（8）计算对应的右特征向量 U（n）。

2 降阶中保留机组集的共享

计算降阶矩阵的外层迭代式（6）中计及特征值的影响，且式（7）采用完整表达，因此特定模式降阶法得到的特征值具有较高的计算精度。但对于省网规模电力系统，需关注的机电模式或弱阻尼模式较多，计算量仍很可观。为减少计算量，进行如下尝试。

尝试1：共享降阶矩阵。初值接近的多个特征值采用式（6）形成的同一降阶矩阵；导致不同初值往往收敛于同一结果，不可行。

尝试2：修正降阶矩阵。先按一个特征值形成降阶矩阵；分析初值接近的其他模式时，按特征值偏差量修正降阶矩阵，由于泰勒级数固有的截断误差，计算误差偏大。

尝试3：共享保留机组。降阶计算时需要确定各模式的保留机组，对应于式（1）中的X1。分析各模式的保留机组情况，对保留机组相同或相近的模式，采用同一保留机组，即共享式（6）中的 A1、A2、A3、A4。 部分减少降阶矩阵的重复计算量。

与λk强相关的机组构成λk的保留机组。强相关机组的确定可依据参与因子或特征值对PSS增益的灵敏度[12]。出于计算速度的考虑，本文采用参与因子评判各机组的参与度。

3 降阶算法的改进实现

3.1 计算效率的改善

降阶过程中的主要计算量由三部分组成：式（6）的复矩阵求逆，式（8）的线性方程组求解，各算式中的矩阵乘法和加法运算。

a.实数化表达。

为避免复数运算中类型自动转换产生的运算量和相应的累计误差，将算式转换为实数表达。

b.采用稀疏技术。

小干扰稳定分析中系统矩阵A的稀疏度与系统结构参数、运行参数和控制方式等因素有关。尽管A的稀疏度不如节点导纳矩阵，但随着系统规模的扩大，稀疏度有所提高。

除特征向量、逆阵（A4-λ（l）I）-1和部分原始参数矩阵外，对矩阵进行稀疏存储。

在稀疏存储基础上进行矩阵乘法和加法运算，并利用因子表技术[1]求解式（8）的线性方程组。

c.利用OpenMP功能方便实现并行计算。

OpenMP是为共享存储的多处理机编写并行程序而开发的应用编程接口[15-16]，由编译器自动完成串行程序的并行化处理，可与Fortran、C或C＋＋结合工作，只要在源代码中插入编译指导语句，并进行少量修改，就可以方便实现并行计算[15-16]。

对于省级电力系统，分析的机电模式较多，利用OpenMP的并行计算模式便于同时使用多核CPU。

3.2 用顺序高斯消去法进行复矩阵求逆

式（6）中的（A4-λ（l）I）-1表示对复矩阵求逆，将其按实、虚部分开，并设其逆矩阵为C＋jD，则有：

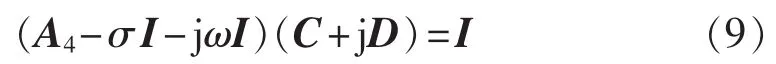
写成实矩阵形式为：

其中，σ、ω 分别为特征值 λ（l）的实部、虚部数值。

对式（10）中的矩阵C和D，可通过反复求解线性方程组得到。然而，式（10）的系数矩阵虽然稀疏，却不能保证对角优势，因此文献[12]、[13]中按主元消去法解线性方程组。

特征值的虚部对应振荡频率，当考虑0.1～2.5 Hz范围的机电振荡模式[1]时，ω 取值 0.628～15.7 rad／s，虚部的绝对值不至于太小。所以对式（10）重新排列，将特征值虚部置于对角位置，如式（11）所示。

这样排列之后，可以采用顺序高斯消去法形成因子表，提高计算效率。

3.3 顺序消去和主元搜索相结合的内迭代计算

式（8）为内迭代算式，其作用是通过迭代得到特征值 λ（m）的右特征向量 U（n）。

由于在内迭代时，矩阵 B-λ（m）I恒定，利用因子表技术提高求解速度。仿照式（11），将式（8）按实、虚部展开，对应特征值虚部的子矩阵置于对角元位置，有：

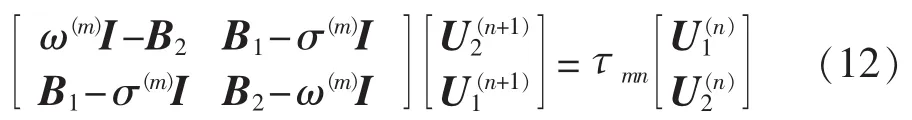
与式（11）相比，式（12）中的对角元素不是仅由特征值虚部构成，不能保证对角优势。

将顺序消去和主元消去结合，在某对角位置出现元素绝对值较小的情况下，搜索该列剩余行的主元，将待消去行与主元所在行交换。如此形成的因子表，既避免了计算失败，又不需要每次消去时都搜索主元。编程实现时考虑到数据类型的精度，将消去法的主元门槛值设为10-5，并利用一维数组记录行交换信息。

3.4 矩阵相乘的稀疏处理

针对次外层迭代算式（7），编程时按三元组（矩阵非零元素值、对应行号及列号）压缩存储矩阵虚部jB2，然后和特征向量相乘；式（6）中，（A4-λ（l）I）-1是稠密矩阵，将 A2、A3稀疏存储后再和（A4-λ（l）I）-1进行计算。由于仅有非零元素参与运算，提高了速度和精度。

3.5 并行计算的采用

随着电力系统规模的扩大，机电振荡模式的数目相应增加。本文借助OpenMP实现多模式特征值的并行计算，对计算程序稍加修改即可实现。

下列示例为Fortran程序中采用OpenMP三线程并行计算的一种格式，其他线程数类似。

OpenMP功能使并行计算的实现变得简单，尤其是在多核微机上同时使用多个CPU。当BLOCK1、BLOCK2和BLOCK3计算程序相同但特征值初值不同时，能同时进行3个降阶模式计算。对于在一个降阶模式计算中使用并行计算技术，需要进一步的算式处理，本文尚未考虑。

4 算例分析

算例数据来源于某省网系统等值，算例1中发电机数为70台；算例2为105台，接近省网规模。发电机采用五阶模型，励磁调节系统、原动机调速系统采用原有模型。系统矩阵A的有关信息如表1所示。

表1给出了状态矩阵阶数、矩阵非零元个数等信息，而算例中稀疏度较高的原因，不仅与运行方式有关，还在于程序中将绝对值小于10-12的元素当作零元素处理。

表1 系统状态矩阵信息Tab.1 Information of system state matrix

本文计算程序在Visual Studio 2008平台的Intel Fortran 11环境下编写，所有变量都采用双精度数据类型；在个别模块（如QR计算）采用记录有效数字位的方法进行乘除运算，减小舍入误差。程序在主频为2.13 GHz的双核计算机上编译运行。

用QR法算出状态矩阵的初始特征值、特征向量，用特征方程校核，最大偏差小于10-7，因此本文按准确值处理。所以算例中只需按最外层迭代算式（6）形成降阶矩阵一次，然后反复进行次外层迭代和内层迭代。

4.1 共享保留机组的分析

研究机电模式时，先根据阈值（本文取各模式最大参与因子绝对值的10%）确定各模式中的强相关机组；然后将强相关机组相同或较为相近的模式归为一类；对每一类包含的若干模式，同时保留与之强相关的所有机组，得到该类各模式降阶分析时可共享的保留机组。

在算例1中，依据强相关机组相同或相近模式归为一类的原则，将69个机电模式分成7类，如表2所示。以表中第1行数据为例，当计算第1类的15个机电模式时，只需采用可共享的17台强相关机组，而不必每次重新确定需保留的机组。

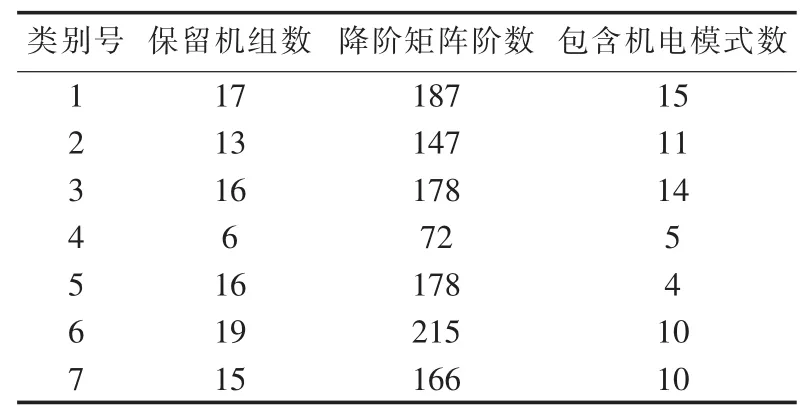
表2 算例1中保留机组信息Tab.2 Information of retained generators in case 1

由上述结果可知，只需要较少的保留机组，就可以实现对所有机电模式的强相关机组划分。在减少降阶计算量的同时，使各模式的分析更加简洁。

4.2 稀疏技术的使用效果

形成降阶矩阵的外迭代算式（6）中，计算量是矩阵求逆和相乘。为验证改进效果，用2种方法实现。

方法1：按本文所述，用稀疏技术计算逆阵，用三元组法处理矩阵运算。

方法2：以主元消去法计算逆阵，满阵存储矩阵并进行相应运算。

表3列出算例1中弱阻尼模式的计算数据。比较计算结果，2种方法所得到的降阶阵数值一致；而稀疏技术的采用，使方法1能较好地节省时间，算例1中求逆和乘法运算的平均时间为5 s（表3中第3、4列之和）。

表3 算例1中弱阻尼模式降阶阵计算数据Tab.3 Calculation data of order reduction matrix under low damping mode in case 1

对于降阶阵实部的QR计算、次外层迭代式（7）、内层迭代式（8），由于矩阵阶数低，耗时较短。算例1中平均用时1.5 s。

因此，对于包含外层迭代、降阶阵实部QR计算、次外层迭代、内层迭代的3重运算，按方法1的稀疏技术进行计算时，算例1的平均耗时约为6.5 s。

4.3 并行计算效果分析

方法3：在采用稀疏技术的基础上，按3.5节的格式编程，实现并行计算。由于算例分析中采用双核计算机，仅可以实现双线程计算。

表4给出了在算例1中方法1和方法3的计算耗时。算例1计算69个模式，在总耗时中计及了确定共享保留机组的时间，但不含程序运行中数据输入、输出时间。

表4 算例1中方法1和3的用时比较Tab.4 Comparison of computation time between method 1 and method 3 in case 1

采用并行计算后，降阶法的计算时间有明显改善。

4.4 算例2

算例2含105台发电机，状态矩阵为1177阶。

类似地，将104个机电模式共分成9类，各类中保留机组的数目在9～21台之间，即计算单个机电模式时的发电机数不超过21台。

仅采用稀疏技术时，即方法1，平均1个振荡模式的计算时间是25.1 s，计算104个机电模式的总耗时为2 612.6s。

进一步结合双线程并行计算，即方法3，平均1个模式的计算时间是13.1 s，计算104个机电模式的总耗时是1358.3 s。

为考核计算效果，本文在算例分析中计算了所有机电模式。对实际系统，仅需计算关注的振荡模式，计算用时会成比例降低；如果进一步采用更多线程，例如利用4核或8核微机，计算时间将进一步减少。

5 结论

特定模式降阶法采用完整表达形成降阶矩阵，能够得出精度较高的特征值。本文对该方法进行了改进。通过研究降阶过程，提出了机电模式共享保留机组集以减少降阶计算量。调整迭代算式采用顺序消去或将顺序消去和主元消去结合，提高计算速度；在矩阵运算中稀疏处理，以节省计算时间。引入OpenMP的并行计算功能，实现多核计算机上对降阶的快速计算。针对省级电力系统的规模，在70机和105机算例中具体讨论了机电模式共享保留机组集的情况，并详细分析了采用稀疏技术和并行计算的改进效果。