赣州市水资源配置方案研究

邱熠晨，栗圆圆

（赣州市水利电力勘测设计研究院，江西 赣州 341000）

1 概述

赣州市位于江西省南部，简称赣南，与广东、福建、湖南接壤，是江西省最大的行政区，现辖1区2市15县，面积3.94万km2，人口918万。赣州市河流众多，集水面积在50 km2以上的有253条，流域分区主要为长江流域赣江上游水系和珠江流域的东江水系、北江水系及韩江。多年平均径流总量336.53亿m3。2010年赣州市供水总量为33.29亿 m3，其中蓄水工程 16.77亿m3，引水工程 10.01 亿 m3，提水工程 4.55 亿 m3，地下水水井供水 1.96 亿 m3。 总用水量为33.29 亿 m3，其中生活用水 4.56 亿 m3，农田灌溉用水 21.84 亿 m3，林牧渔业用水 2.61 亿 m3，工业用水 4.03 亿 m3，生态环境用水0.25 亿 m3。

本文以2010年 《赣州市统计年鉴》、《赣州市水资源公报》为主要信息来源，对赣州市初始水资源配置进行研究，运用层次分析法及单元系统模糊优选模型相结合的方法确定赣州市初始水资源配置方案，使配置方案既有利于提高赣州市整体经济效益和社会效益，又能让不同行政区域普遍接受。

1 层次分析法进行水资源配置

水资源流域性的特点决定了水资源必须按流域进行统一管理。通常情况一个流域涉及几个不同行政区域，在不同的行政区域间合理分配有限的水资源是流域管理的重点研究方向，如何使水资源配置做到既兼顾效率又体现公平是当前学者和决策者研究的热点和难点问题。

层次分析法（AHP）是美国学者 T.L.Satty 于 1973年提出的一种系统分析方法[1]，该法是从定性分析到定量分析综合集成的典型系统工程方法，目前被广泛应用于多因素权重的确定。

2.1 水资源初始分配的方法

水资源的初始分配通常分为两个层次：第一层次为从流域到行政区域的分配；第二层次为从行政区域到不同用水部门的分配。本文主要探讨水资源第一层次的分配。在运用层次分析法分配水资源的过程中，其初始分配原则、指标体系的构建是十分重要的。

2.1.1 初始分配原则

赣州市的水资源分配需要考虑社会、经济、环境等多方面因素，影响这些因素的指标有很多。本文对水资源进行初始分配采用有效性、公平性和可持续性原则[2]，即通常所说的三性原则。

2.1.2 指标体系构建

结合赣州市各地区水资源量及社会经济的特点，其指标体系主要包括经济发展、投资贡献、水量贡献、用水指标、水质状况、绿化面积等[3]。赣州市水资源初始分配指标体系层次结构见图1。

2.1.3 各个指标相对权重

各指标相对权重的计算可通过各层次指标进行相互对比，确定相对重要性并赋值；再根据赋值来构造判断矩阵，用和法确定矩阵的最大特征值，该值所对应的特征向量即为各层次、各指标的权重，最后检查其权重是否满足一致性要求。各矩阵构造及指标权重具体计算如下：

1）目标～准则层次判断矩阵及层次指标权重

该层次涉及指标包括有效性、公平性和可持续性指标。在进行比较时通常考虑公平性更为重要，经指标相互比较后赋值构建判断矩阵Q1。如下：

建立方程：Q1ω1＝λω1，采用和法计算可得 ω1＝3.005。经对判断矩阵进行一致性检验可知，CR＝0.0043，满足判别要求。

2）准则～指标层次判断矩阵及层次指标权重

①有效性～指标层次仅涉及经济发展指标。由于只涉及一个指标，权重数ω2＝1。且认为满足一致性要求。

②公平性～指标层次涉及指标包括投资贡献、水量贡献及用水量指标。经指标相互比较赋值后构建判断矩阵Q3。如下：

建立方程 ：Q3ω3＝λω3，采用和法计算可得ω3＝3.0003。经对判断矩阵进行一致性检验可知，CR＝0.00026，满足判别要求。

③可持续性～指标层次涉及指标包括水质状况及绿化面积指标，其判断矩阵Q4如下：

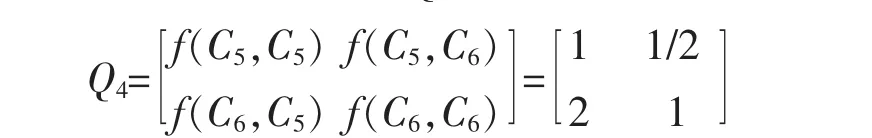
建立方程 Q4ω4＝λω4，经和法计算可得 ω4＝1，由阶数为2可知该矩阵是一致的，满足判别要求。

3）指标～分指标层次判断矩阵及层次指标权重

①经济发展～分指标层次涉及指标包括国内生产总值、农业总产值及工业总产值指标，其判断矩阵Q5如下：

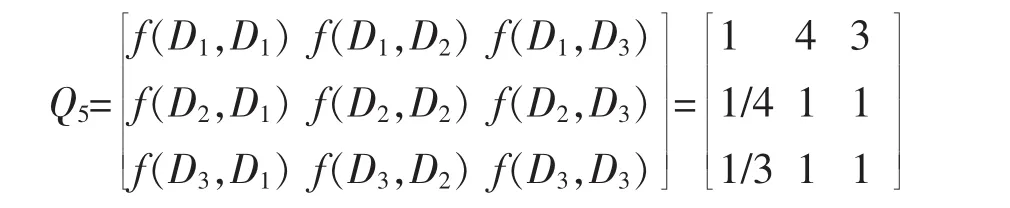
建立方程：Q5ω5＝λω5，采用和法计算可得 ω5＝3.009。经对判断矩阵进行一致性检验可知，CR＝0.0077，满足判别要求。

图1 赣州市水资源初始分配指标体系层次结构图

②投资贡献～分指标层次仅涉及固定资产投资指标。由于仅涉及一个指标，权重数ω6＝1。满足一致性要求。

③水量贡献～分指标层次仅涉及多年平均降水量指标。由于仅涉及一个指标，权重数ω7＝1。且满足一致性要求。

④用水指标～分指标层次涉及指标包括工业万元增加值用水量、城镇公共用水量、居民生活用水量及农业用水量指标，其判断矩阵Q8如下：

建立方程：Q8ω8＝λω8，采用和法计算可得 ω8＝4.021。经对判断矩阵进行一致性检验可知，CR＝0.012，满足判别要求。

⑤水质状况～分指标层次仅涉及工业废水排放未达标率。权重数ω9＝1。且满足一致性要求。

⑥绿化面积～分指标层次仅涉及森林覆盖率。权重数ω10＝1。且满足一致性要求。

根据上述分析计算，可求得最终各指标的相对权重，详见表1。

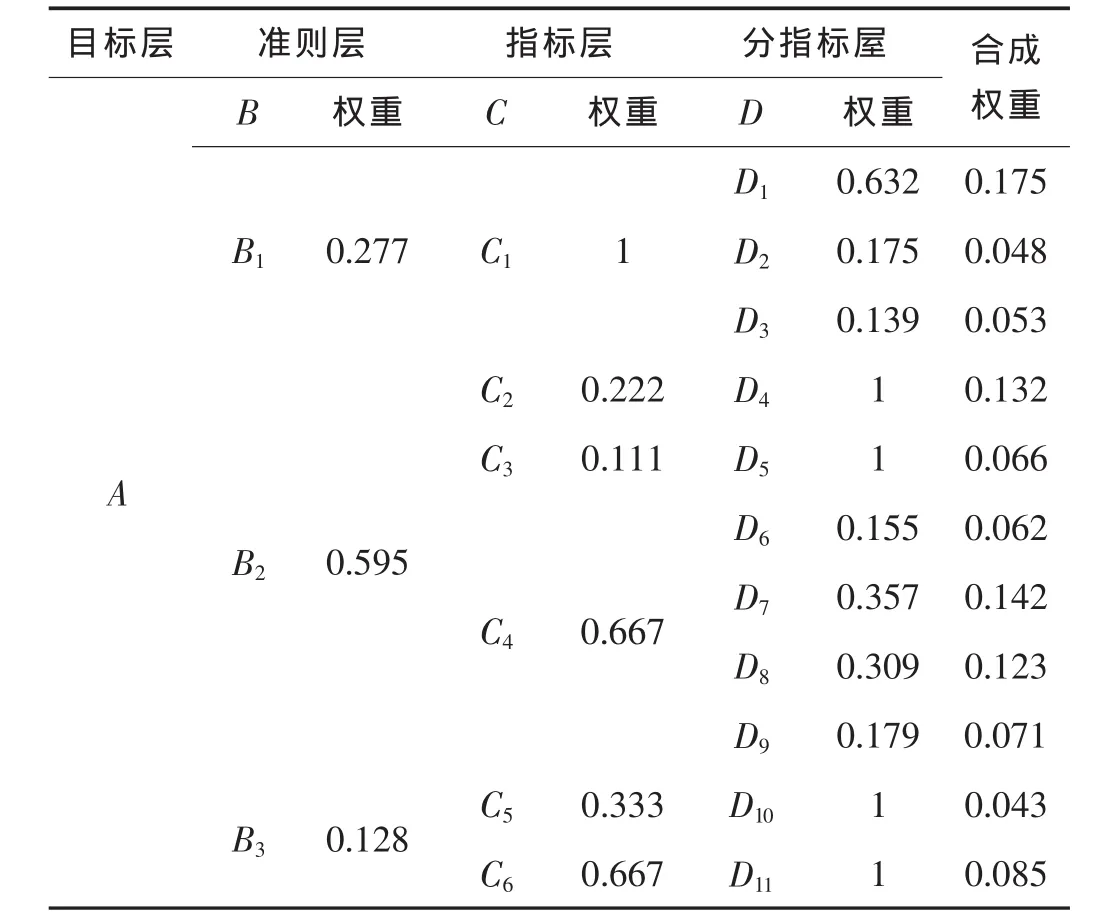
表1 初始水权分配各层指标权重

2.1.4 建立单元系统模糊优选模型

设立方案集 E＝（E1，E2，…En）＝（区域 1，区域 2，…，区域n）。对于定量目标，越大越优型的优属度公式如下：

越小越优型的优属度公式如下：

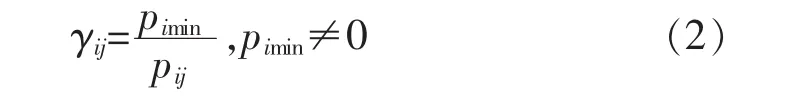
式中：pij—j方案目标特征值；

γij—j方案i目标的相对优属度。

上述优属度矩阵可以得到优等方案g与劣等方案b。系统中的每个方案分别以一定的隶属度属于优等方案或劣等方案。

方案j的相对优属度μj值按如下公式计算：

式中djg为方案j与优等方案的距离，本文计算采用广义欧氏距离[4]：

djb为方案j与劣等方案的距离，本文计算采用广义欧氏距离：

最后将最高层次方案对于优的隶属度向量归一化，可得到赣州市各县（市）水资源初始分配权重，将水资源初始分配的总向量与分配权重相乘，即为各地区分配得到的初始水资源量。

2.2 第一层次初始分配

赣州市下辖18个县市区，初始水资源分配总量为48.3 亿 m3。 根据上述分析，准则集 D＝（D1，D2，..D11）和方案集 E＝（E1，E2，..E18）。

2.2.1 相对优属度及各地区水量配置权重的计算

目标特征值Pij的值参见表2。

由公式（1）可求得相对优属度的矩阵，计算结果见表3。

由表 3 可得，优等方案向量 g＝（1，1，… ，1）T，劣等方案向量 b＝（0.1，0.15，0.17，0.07，0.07，0.05，0.06，0.07，0.03，0.06，0.11，0.2，0.13，0.07，0.01，0.05，0.1，0.13）T将优等方案向量与劣等方案向量分别代入公式（4）、（5）即可得djg与djb，再由公式（3）可求得各方案的相对优属度的值 μj，将向量（μ1，μ2，…μn）归一化，可得到水资源初始分配到各县市权重见表 4。

表2 目标特征值

表3 相对优属度矩阵

表4 赣州市水资源量对各县市的分配及其排序

2.2.2 水资源量的分配

赣州市可分配水资源总量为48.3亿m3，将各县市的权重数与可分配水资源总量相乘即得各地区水资源量分配结果，详见表4。

3 结果分析

根据赣州市水资源量分配计算的结果可知，E1（章贡区）分配的水资源量最多，说明水资源量的分配与国民生产总值正相关。E12（于都县）、E3（信丰县）等县分配水资源量相对较多，这主要是由于这些县农田面积较大，农业相对来说比较发达。而有一些计算结果与实际情况略有偏差，如E17（瑞金市）和E18（南康市）同属工业城市，其分配水量相差较多，E15（寻乌县）和E16（石城县）工业、农业状况相近，分配水量也相差较多。产生这些偏差的原因来源于《赣州市水资源公报》在工业用水量、农业用水量、废水排放未达标率等指标的调查统计可能存在一定误差，导致本次分配结果可能与赣州市各县市实际用水情况不完全一致，这些问题有待进一步研究。本文可为赣州市水资源量分配提供一种方法，同时对赣州市水量分配方案具有一定的参考价值。

［1］Satty T L.The analytic hierarchy process ［M］.New York：Mccraw－Hill，1980.

［2］Singh，Chhatrapati.Water Rights and Principles of Water Resources Management［J］.Water Resources Development，2009，17（1）：55－78.

［3］WALSH M R.Toward spatial decision support systems in water resources［J］.Water Resources Planning，2009，109（2）：158－169.

［4］唐 健，黄健元.模糊优选模型及应用［J］.大学数学，2005，21（6）：71－76.