多维时间序列因变量的快速定阶及其害虫发生量预测

徐镜善 ，王 凯 ，袁哲明

（1.湖南大众传媒职业技术学院，湖南 长沙 410100；2.湖南农业大学植物保护学院，湖南 长沙410128；3.湖南农业大学作物种质创新与资源利用国家重点实验室，湖南 长沙 410128）

害虫发生量不仅受多种外在因素（如气象，生理，生态等）影响，而且与其历年发生动态极其相关，属于典型的多维时间序列复杂非线性数据[1-2]。传统自回归模型（Autoregressive，AR）假定当年观察值是过去p年（p为阶次）观察值的线性组合，但仅能用于一维时间序列分析且无法给出拓阶上限，而地统计学（Geostatistics，GS）中半变异函数模型的后效时间长度可实现一维时间序列自动快速定阶[3-4]。带控制项的自回归滑动平均模型（Controlled Autoregressive Integrating Moving Average，CARMA）及带受控项的自回归模型（Controlled Autoregressive，CAR）等已应用于多个多维时间序列分析，但由于其线性本质，导致应用受限[5-7]。基于结构风险最小的支持向量机（Support Vector Machine，SVM）以统计学习理论为基础，较好地解决了局部最小、过学习、非线性等问题，有效应用于复杂非线性数据系统的建模预测[8-11]。研究结合地统计学半变异函数模型与支持向量回归（Support Vector Regression，SVR），实现多维时间序列的因变量自动定阶与自变量非线性筛选，并应用于2种害虫发生量预测。

1 原理与方法

1.1 数据预处理

多维时间序列因变量yt若具有明显的上升或下降趋势，则需要对其进行去趋势平稳化处理。研究采用对数线性去趋势（Log-linear De-trending，LLD）平稳化法对因变量进行平稳化处理[12]：首先，对因变量yt取自然对数得lnyt；其次，以lnyt与时间t建立一元线性回归方程lnyt=a+bt，求解得截距a与回归系数b，以时间t为自变量回带可得预测(Inyt)′；最后，对数线性去趋势平稳化后的因变量为：

由于支持向量机程序LIBSVM[13]对自变量取值较为敏感，所以将多维时间序列自变量根据式（2）规格化到-1到1的区间：

以平稳化处理后的因变量yt与规格化后的自变量xi进行后续分析。

1.2 地统计学后效时间长度

地统计学主要研究在空间分布上既有结构性又有随机性的自然现象，其以区域化变量理论为基础，以半变异函数为主要工具[3-4]。对于多维时间序列因变量观测值y(t)，t=1，…，，其实验半变异函数值r(h)可用下式计算：

式（3）中，h是两个观测值之间的时间间隔，N(h)是相隔时间为h的数据对y(t)和y(t+h)的对数，y(t)和y(t+h)分别是时间t和时间t+h的观测值。假定两个观测值间最大时间间隔为max(d)，为保证N(h)充分大，一般规定h≤max(d)。

半变异函数曲线常可用球状模型拟合：

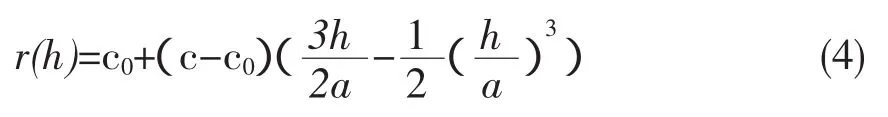
式中，c0为块金值，c为基台值，a为变程，即r(h)达到基台值时的间隔距离h，它表示在h≥a以后，区域化变量的空间相关性消失。因此，对某个待测点的估计，应根据其距离a以内的已知点来进行。袁哲明等[14-15]将半变异函数模型应用于一维等间隔时间序列，研究了二化螟与三化螟种群的时间格局。半变异函数模型的变程a对应于时间序列分析的后效时间长度，根据变程a可实现多维时间序列因变量的快速定阶。

1.3 因变量与自变量定阶

设已平稳化处理的多维时间序列为（yt，xij），t=1，2，…，n；j=1，2，…，m；其中 n 为样本数，m 为自变量个数。首先，根据CAR对多维时间序列原始自变量拓且仅拓一阶，则训练集样本个数变为n-1，自变量个数变为2m；其次，对多维时间序列因变量计算半变异函数，为避免拟合半变异函数曲线带来的拟合误差及额外计算量，设定的时间间隔范围内最大半变异函数值r(h)对应的h即为后效时间长度a，因变量拓展a阶后训练集样本个数变为n-1-a，自变量个数变为2m+a。

1.4 支持向量回归非线性变量筛选

SVR核函数的选择一般是经验性的，径向基核函数在多数数据集上比其他核函数（如线性核、二项式核等）表现优异[16]，因此研究采用径向基核作为SVR建模核函数。对于训练集（yt，xij），t=1，2，…，n-1-a；j=1，2，…，2m+a，首先对 2m+a 个自变量经10次交叉验证搜寻最优SVR参数，对应均方误差（Mean Squared Error，MSE）记为 MSE0；其次，依次剔除第 j个自变量得 MSEj，若 min[MSEj]＜MSE0，则剔除最小MSE对应的自变量，进入下一轮筛选（此时自变量个数变为2m+a-1），反之，非线性变量筛选过程结束；最后，保留自变量用于后续SVR建模。为方便后文参比，将该自变量筛选方法命名为Support Vector Regression-Nonlinear Variable Screening（SVR-NVS）。

1.5 一步预测及模型评价指标

此时训练集为（yt，xij），t=1，2，…，n-1-a；j=1，2，…，s；s为保留自变量个数。以径向基核函数为基础，对训练集经10次交叉验证搜寻最优参数，根据确定的最优参数建立SVR模型。对第1个待测样本，依训练集确定的阶次与保留自变量构建新的测试样本，以SVR模型预测该样本，根据式（1）反推得最终预测值。预测第2个待测样本时，第1个测试样本需加入到训练集中，此为一步预测。由于训练集有改变，所以需要重新拓阶及变量筛选。

模型的独立预测精度采用均方根误差（Root Mean Square Error，RMSE）作为评价指标：

1.6 参比模型

为了体现研究方法的优势，需要与已有的模型进行参比。研究参比了4种模型，其中包括基于SVR的非线性模型SVR-NVS与SVR，参比线性模型包括多元线性回归（Multiple Linear Regression，MLR）与逐步线性回归（Stepwise Linear Regression，SLR）。所有模型均在MATLAB（2012a）环境下实现。

2 结果与分析

2.1 稻纵卷叶螟二代高峰日蛾量预测

数据来源于江苏省通州市1973~1997年共25 a的西太平洋副高及稻纵卷叶螟二代高峰日每66.7m2蛾量Y[17]，对应的预报自变量为副高的面积指数（X1），强度指数（X2），西伸脊点位置（X3，经度），脊线位置（X4，经度），北界位置（X5，纬度）（表 1）。

表1 稻纵卷叶螟二代高峰日蛾量

研究以1973～1987年15 a的数据为训练集，1988～1997年间10 a数据作为独立测试集。各年份的观测值及各模型预测值见表2，均方根误差RMSE预测指标见表3。由表3可知，该研究预测所得RMSE值在所有参比模型中最小，说明所建模型稳定性及外部预测能力最好。由表2可知，除了1988年、1993年、1994年这3 a的蛾量预测值与观测值偏差较大，其他年份的预测偏差均较小；对1988年的蛾量预测，MLR与SLR线性模型的预测值比基于SVR建立的非线性模型预测值更加接近观测值，说明了当年数据各因素间的线性本质；对1993年的蛾量预测，MLR与SLR预测出了负值，表明当年数据仍用线性模型预测是不合理的。对最后3年即1995～1997年的蛾量预测，该研究方法比其他参比模型的预测偏差大幅减小。因此，该研究方法所建模型在整体上优于其他参比模型，显示了因变量快速定阶以及一步预测法的优势。

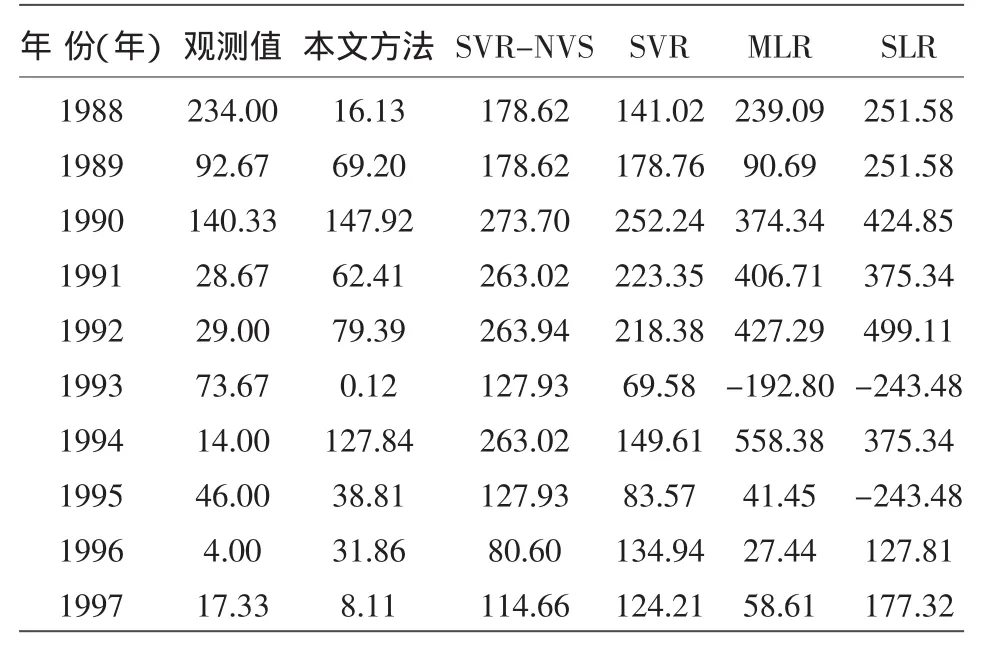
表2 稻纵卷叶螟二代高峰日蛾量观测值及预测值

表3 参比模型均方根误差RMSE值

2.2 晚稻第五代褐飞虱发生量预测

第五代褐飞虱是晚稻生长期间的主要害虫，提高褐飞虱发生量预测准确度，及时采取有效防治措施，对于晚稻丰收至关重要。数据来源于浙江省杭州市萧山区1974～2005年晚稻第五代褐飞虱的发生量[18]。

以1974～2000年多维时间序列数据为训练集，2001～2005年为独立测试样本，各年份的观测值及各个模型预测值见表4，均方根误差RMSE值见表3。由表4可知，该研究方法对各年份的预测精度明显优于其他模型。对2001年褐飞虱的发生量预测值比其他SVR非线性模型的预测值精确了将近一个数量级，也优于SLR模型，与MLR模型预测准确度相当；对2002年、2003年的褐飞虱发生量进行预测，该研究方法预测值较其他4个参比模型明显接近真实观测值。

表4 晚稻第五代褐飞虱发生量观测值及预测值

3 结论

以地统计学半变异函数模型的后效时间长度为指导，实现了多维时间序列因变量的自动、快速定阶，并结合SVR非线性筛选自变量，以一步预测法成功应用于2种害虫发生量的预测。该方法具有地统计学半变异函数模型对因变量定阶自动化、快速的优点，适合时间序列分析；同时具有SVR结构风险最小、非线性、有效避免过拟合与局部最小、外部预测能力优异等优点，适合多因素非线性回归分析。经试验表明，该研究方法可有效应用于害虫预测预报。

[1]吴承祯，洪 伟.林木生长的多维时间序列分析[J].应用生态学报，1999，10（4）：395-398.

[2]周立阳，费惠新，张孝羲.多维时间序列分析在稻纵卷叶螟长期预测预报上的试用[J].植物保护学报，1995，22（1）：1-6.

[3]李哈滨，王政权，王庆成.空间异质性定量研究理论与方法[J].应用生态学报，1998，9（6）：651-657.

[4]Liebhold A M，Rossi R E，Kemp W P.Geostatistics and geographic information systems in applied insect ecology[J].Annu.Rev.Entomo，1993，（38）：303-327.

[5]Box Q E P，Jenkins G M.Time series analysis：forecasting and control[M].San Francisco：Holden-day Press，1970.

[6]Hannan E J.The estimation of the order of an ARMA process[J].Ann.Statist，1980，8（5）：1071-1081.

[7]邓自立，郭一新.动态系统分析及其应用[M].沈阳：辽宁科学技术出版社，1985.31-130.

[8]V Vapnik.The nature of statistical learning theory[M].New York:Springer Verlag Press，2001.

[9]邓乃扬，田英杰.数据挖掘中的新方法－支持向量机[M].北京：科学出版社，2004.

[10]马晓光，胡 非.利用支持向量机预报大气污染物浓度[J].自然科学进展，2004，14（3）：349-353.

[11]Ping F P，Wei C H.Support vector machines with simulated annealing algorithms in electricity load forecasting[J].Energy Conversion and Management，2005，46：2669-2688.

[12]王海燕，卢 山.非线性时间序列分析及其应用[M].北京：科学出版社，2006.139-141.

[13]Chang C C，Lin C J.LIBSVM:a library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology(TIST)，2011，2（3）：27.

[14]袁哲明，付 威，李方一.二化螟种群空间格局的经典分析与地统计分析比较研究[J].应用生态学报，2004，15（4）：610-614.

[15]Yuan Z M，Wang Z，Hu X Y.Geostatistical analysis on the temporal patterns of the Yellow Rice Borer.Tryporyza incertulas[J].Rice Science，2005，12（3）：207-212.

[16]陈 渊，袁哲明，周 玮，等.基于地统计学与支持向量回归的QSAR 建模[J].物理化学学报，2009，25（8）：1587-1592.

[17]汪四水，张孝羲.害虫预测建模中的因子综合[J].南京农业大学学报，2000，23（2）：35-38.

[18]陈水校.简易多级法预测晚稻第五代褐飞虱发生量[J].江苏农业科学，2006，（4）：48-50.