基于粗糙集的银行存货质押业务投资决策研究

苏国振，何 娟

（西南交通大学交通运输与物流学院，四川成都 610031）

中小企业是推动国民经济发展的重要力量，在吸纳城乡劳动力就业、完善市场经济体制等方面有着不可替代的作用［1］。然而金融危机以来，中小企业发展面临巨大挑战，尤其在融资方面，由于其高动产、低资信的结构特点，普遍面临“融资难”的问题。但是另一方面，金融竞争和资本充足率约束使得依赖传统业务的银行盈利空间缩小，急需开发新的业务提高盈利水平［2］。供应链金融业务的出现，较好地解决了上述矛盾问题，吸引了国内外众多银行，甚至部分企业积极开展此类业务。存货质押业务是供应链金融的核心业务，也是众多银行广泛开展的业务之一。存货质押是指企业将库存产品、半成品及原材料等作为担保，向银行出质，同时将质物转交给具有合法保管动产资格的第三方物流企业监管，以获得银行贷款的业务活动［3］。其业务操作流程见图1所示。

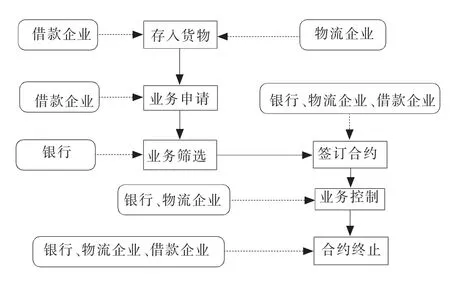
图1 存货质押业务流程图Fig.1 Flow chart of inventory financing

存货质押业务的广泛开展吸引了众多学者进行研究，在定性和定量研究方面取得了很多成果。定性研究方面，李毅学等讲述了存货质押业务的演化过程［4］，将供应链金融的复杂风险归纳为系统和非系统2大类，基于供应链金融风险评估的原则构建了评估指标体系［5］。在定量研究方面，存货质押的现有理论侧重于质押业务中质物质押率的确定、风险定价以及对企业的影响研究。例如：李毅学等讨论了存货价格服从随机波动和企业违约率有重随机特征下的银行质押率决策［6-7］；JOHN等从企业的角度首次将资产抵押融资集成到企业的生产决策中，研究了资产抵押融资业务中贷款利率和质押率的确定，以及对企业和银行盈利的影响［8］；BERLING等研究了当期末价格随机波动时，融资企业的库存决策问题和违约风险问题［9］。

受供应链协调机制设计以及委托代理理论研究的影响，国内学者开始从多方决策方面基于博弈论和委托代理理论来研究存货质押非合作方的博弈行为。其中基于银行的角度，李娟等通过完全信息动态博弈表明，银行对物流企业施以激励比激励借款企业更能减少业务风险［10］；何娟等引入不完全信息下的重复博弈理论，证明银行应与物流企业建立长期合作关系，以减少物流企业与借款企业的合谋风险［11］；李毅学等讨论了信息不对称的情况下，银行如何防范物流企业与借款企业共谋，即变委托严密监管为简单监管，欺诈银行的行为［12］；马中华等从物流企业决策角度，考虑银行与企业之间的委托代理关系，定量给出物流企业的参与条件及其监管决策［13-14］。

然而，无论是质押率的确定还是风险定价等，学者们的研究多是从业务的“部分”出发，研究业务的某一方面，制定一些措施来减少风险，达到促进业务达成的目的。但是银行在面临某业务时，应该放贷或是惜贷，学者们的研究却少之又少。决策粗糙集自研究人员在1990年提出以来［15］，已经在医学诊断、邮件分类以及石油投资等众多领域得到了广泛的应用［16-18］。本文基于存货质押业务中的主导者银行，运用粗糙集的方法，引入3支决策的思想，通过不同情况下银行的收入和支出来确定损失函数，从而计算出决策粗糙集的阈值，通过与先验概率的比较，使银行得出最优决策。存货质押业务中，引入3支决策的思想，即银行不止是只考虑放贷和惜贷，在一定情况下，要结合进一步的调查而作出决策，这正是3支决策粗糙集中的延迟决策思想。因此，将3支决策粗糙集引入到存货质押业务的决策中，有一定的理论和现实意义。

1 决策模型的建立

1.1 决策粗糙集基本思想［19］

假设S＝（U，A，V，f）是一个信息表，∀x⊆U，0≤β＜α≤1，则（α，β）-下近似集、（α，β）-上近似集可分别定义为

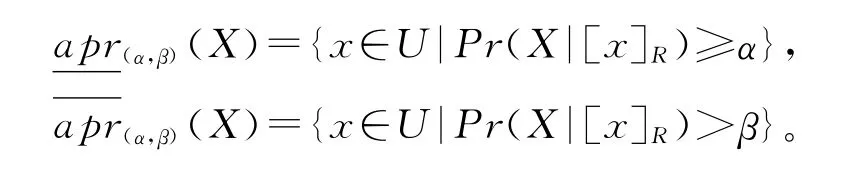
（α，β）-上、下近似集可将论域分为3个部分，正域、负域和边界域，其定义如下：

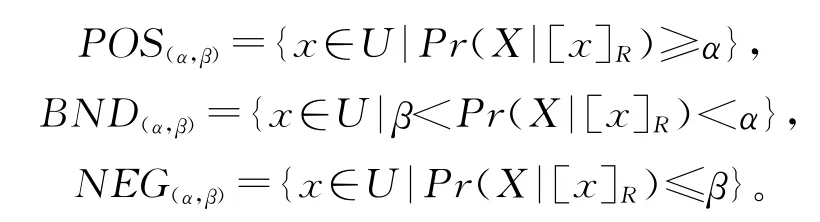
1.2 模型基本假设与参数设定

1.2.1 问题描述与基本假设

不同于银行普通的贷款业务，存货质押业务一个明显的特征是其抵押物是动产，动产的价格会随着市场供需等因素的变化发生变化。当抵押动产价格下降、其价值已不足以偿还贷款时，就会发生借款企业违约的风险。另外，通过上述业务流程可以发现，存货质押业务是一种涉及多方的交易行为，参与方包括银行、借款企业、物流企业。在此业务模式下，存货质押业务除了具有一般贷款业务的风险特征外，还存在一些特有的风险特征，具体表现在风险因子已不仅仅局限于各方参与主体自身，还表现为各方参与主体交易的相互作用带来的衍生风险以及风险传导带来的综合性风险。例如：在交易中，物流企业掌握了质押货物的信息，受交易成本和信息不对称的影响，物流企业可能为了眼前利益，与借款企业合谋，帮助借款企业欺骗、隐瞒银行，而作为主要风险承受方的银行就有可能遭受很大的损失。以上存货质押风险为银行业务投资选择提出了新的挑战。但从另外一个角度出发可知，风险与收益成正比，在某业务中，只要银行认为其潜在收益大于企业违约带来的损失，银行就会接受该业务。但是，与普通贷款业务不同的是银行要与物流企业共享收益，另外还要预防物流企业与借款企业合谋带来的损失。

因此，在存货质押业务筛选中，是否执行该业务主要在于它的期望损失值。一个存货质押业务的执行结果可能有2种情况：一是借款企业不违约，业务成功；另一种结果是企业违约而导致业务失败。如果企业不违约，则银行期望损失值为负，反之则为正。银行的损失函数大小主要取决于2个方面：一是借款企业所付的利息，即业务的收入；另一方面是支出，包括2部分，一部分是业务中所有人员以及机会损失等一切费用，另一部分是业务达成支付给物流企业的监管费等费用。对于银行而言，需要的是选择期望损失最小的业务作为投资项目。基于此，对于业务作出以下假设：

1）银行资金充裕，如果不投资项目，则该笔资金将不产生任何收益；

2）对于借款企业而言，企业在项目成功后盈利一定会偿还贷款本息，而项目失败后企业一定违约，但不存在恶意违约情况，即项目成功率和借款企业偿还贷款概率相同；

3）在业务操作过程中，物流企业基于对质押物信息作全面了解，为借款企业提供一定的质押担保，即借款企业在不能偿还贷款后，物流企业提供质押物的拍卖担保，拍卖所得归银行所有，以抵补银行损失；

4）为和物流企业建立良好合作关系，防止物流企业与借款企业合谋，银行每成功一笔业务就出让部分利息收入，作为对物流企业的激励；

5）银行若针对某项目作延迟决策，则经延迟决策后需要确定投资或者拒绝该项目。

1.2.2 模型假设与参数设定

根据决策粗糙集理论以及上述假设，存货质押业务决策问题可用2个状态集和4个行动集来描述决策过程，状态集Ω＝｛X，-X｝分别表示贷款企业不违约和违约2种状态；行动集A＝｛aP，aBP，aBN，aN｝分别表示银行投资、延迟投资、延迟不投资、不投资4种行动。另外假设论域为U，xi∈U代表某项业务，其等价类Ui＝［xi］R是指具有相同属性的某一类业务。记θPP，θBPP，θBPN，θNP，φPP，φBPP，φBPN，φNP分别表示某项业务中借款企业不违约时，银行采取行动aP，aBP，aBN，aN时的收入和支出；θPN，θBNP，θBNN，θNN，φPN，φBNP，φBNN，φNN分别表示某项业务中借款企业违约时，银行采取行动aP，aBP，aBN，aN时的收入和支出。在模型中，为方便分析，只考虑借款企业完全偿还本息和完全不偿还2种情况，对于模型中的参数，作出以下设定：

1）假设B为质押物价值，本文中通过前期投入和期末收入确定损失函数，因此质物在业务运行过程中的波动暂不考虑，只关注企业违约时质物变现的比率；

2）银行根据物流企业提供的质物信息，设定R为质押物的质押率，r为业务中的贷款利率；

3）c1为业务考察费用，包括设计业务考察的人员、运作等一切支出，假如银行针对某项业务作延迟决策，则业务需2次考察，考察费为cy；

4）c2为监管费用，与质物价格成正比，c3是银行为防止物流企业与借款企业合谋，在业务成功后支付物流企业的奖励；

5）如果借款企业违约，质物将被拍卖变现，α为质物变现率，变现所得归银行所有，物流企业只得到监管费而无法获得银行的激励奖金；

6）假设银行为风险中性，若银行延迟决策时不作任何投入，则其判断准确的概率为0.5。此处，有一个符合现实的情况为银行延迟决策时，随着投入的增加，其决策的精确度p越高；又因为事物的不确定性，无论投入增加到多大，精确度p＜1。其函数符合图2所示。

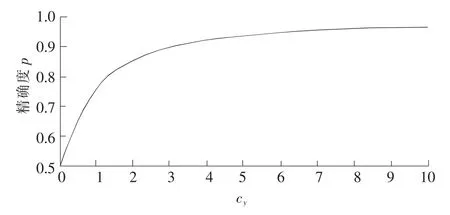
图2 考察投入与判断精确度关系图Fig.2 Input investigation and the decision accuracy diagram

从图2可以发现，p和cy符合类正切关系，因此，此处假设：

1.2.3 支函数的确定

银行在存货质押业务操作中，可确定在采取不同策略时期末借款企业违约与不违约时的收入和损失，模型中θgP表示企业不违约时投资后的收入，由于银行资金充裕，因此企业不违约时延迟投资和投资收入相同，为借款企业所付的利息，即θPP＝θBPP＝BR（1＋r）。θNP＝θBNP＝0，表示没有投资该项目，因此没有任何收入；θgN表示企业违约时投资后的收入，θPN＝θBPN＝Bα，表示银行投资某项业务，但借款企业违约，质物被拍卖，银行期末只能收入拍卖所得；θNN＝θBNN＝0，表示银行考察发现，业务存在违约风险，没有投资该项目，收入为0。

银行每进行一项业务，都要对其考察，需要支付一定的考察费用，当银行决定投资某业务时，需要向物流公司支付存货的监管费，并且为了维持与物流公司的良好合作，防止物流企业与借款企业合谋，每做成功一项业务，银行将出让部分利息收入作为对物流公司的激励。按照此原则，计算银行采取各种投资措施下的支出。φgP表示借款企业不违约时银行的支出，其中，φPP＝c1＋c2＋c3＋BR，φBPP＝c1＋c2＋c3＋cy＋BR，表明延迟决策的情况下银行要多支出部分考察费，φNP＝c1＋BRr，表明银行错误地拒绝了潜在带来收益的项目，设定支出包括考察费与资金的机会成本损失；φgN表示企业违约时银行的支出，其中φPN＝c1＋c2＋BR，φBPN＝c1＋c2＋cy＋BR，表示银行决策失误，错误地接受了违约的业务，期末银行损失了本金，并且支付一定的考察与监管费用；φBNN＝c1＋cy，φNN＝c1，表示银行成功拒绝了潜在违约业务所支付的考察费。

1.3 阈值的确定

收入与支出确定后，银行投资或者拒绝某业务的情况下损失函数分别为

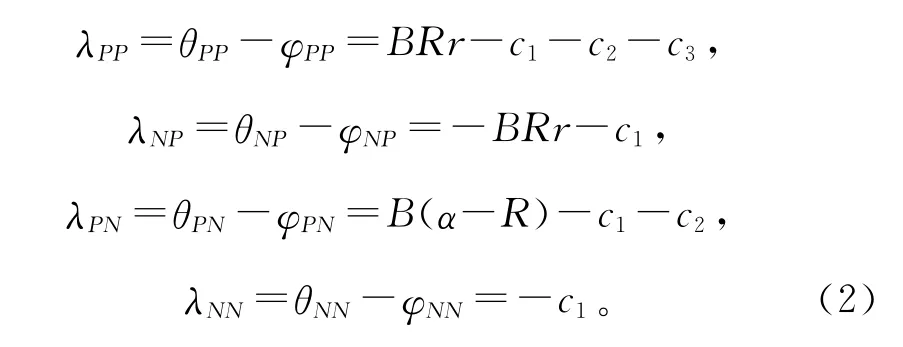
银行延迟投资时，延迟决策关于投入与判断精确度的函数如式（3）所示：

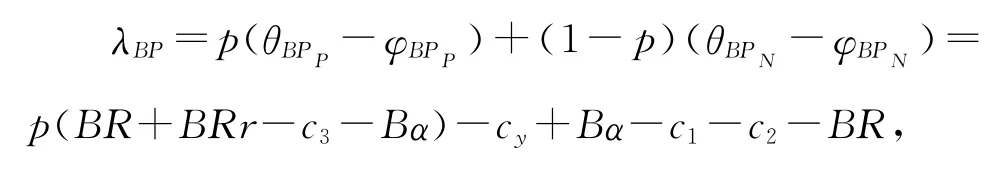
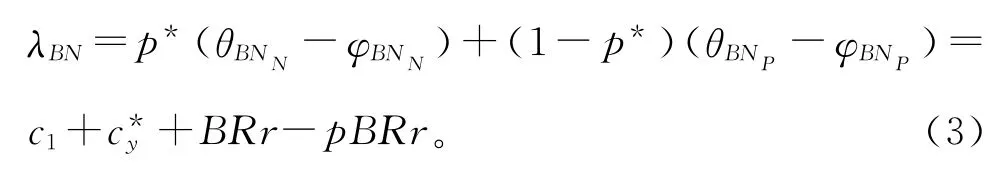
由于投入和判断精确度满足式（1），将式（1）代入到式（3）中，则λBP，λBN是cy的函数，对其求导，然后令导数等于0，可得λBP，λBN最优时的银行投入，分别为

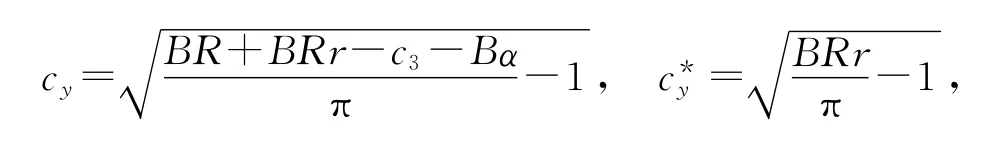
从而可求得最优的λBP，λBN分别为

则采取aP，aB，aN这3种行动下的期望损失可分别表示为

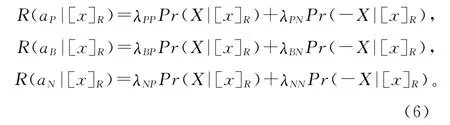
现实决策中，理性人会选择期望损失最小的行动集作为行动方案，因此可得到如下3条决策规则：

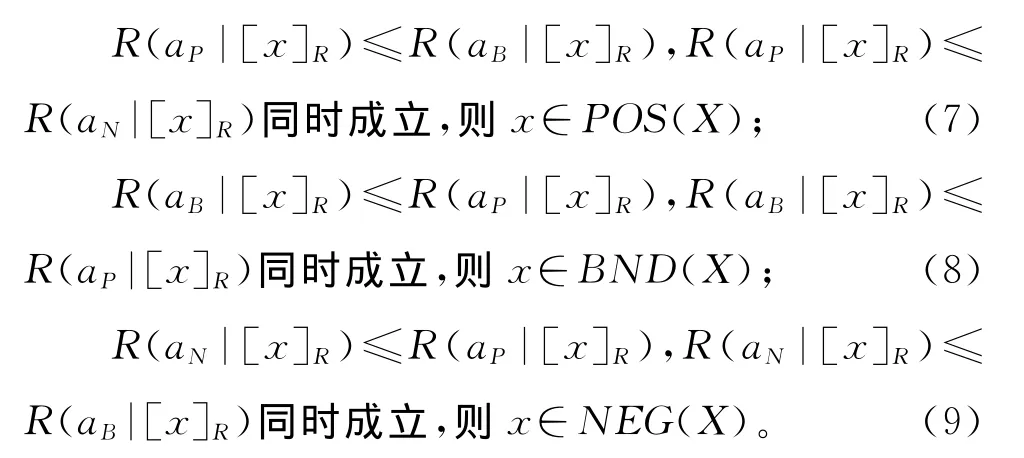
由于X和它的补集-X发生的概率之和为1，所以有

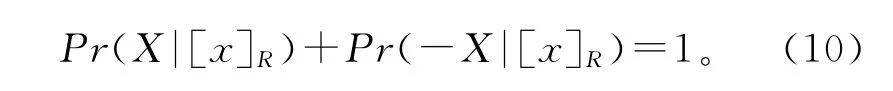
将式（10）代入式（6）中，然后将所得结果再分别带入式（7）—式（9），可得到如下结果。

对规则（7）：

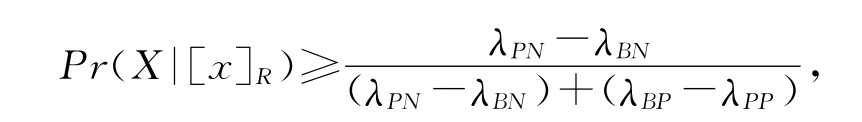
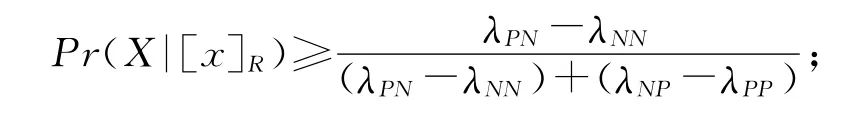
对规则（8）：

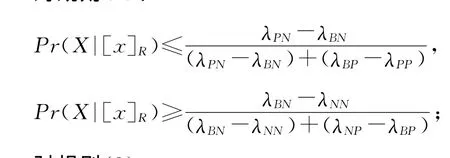
对规则（9）：

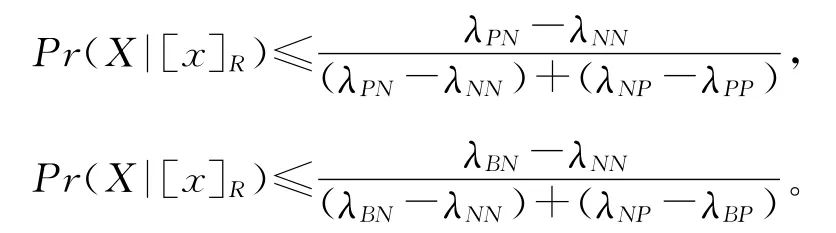
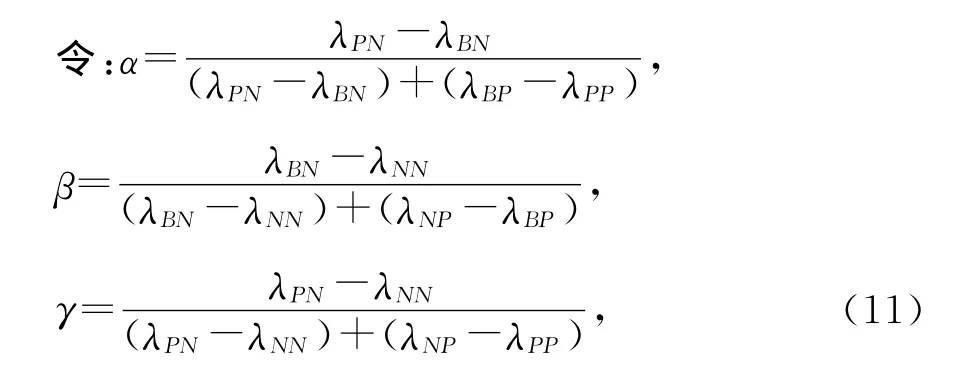
将损失函数λPP，λBP，λNP，λPN，λBN，λNN分别代入，即可求出3条决策时的阈值α，β。

1.4 先验概率的确定方法

银行在业务操作过程中，积累了大量的数据，根据这些数据建立信息表S＝（U，A，V，f），先验概率正是基于历史业务数据得到的。首先，在信息表中，可直接获得的数据如下：

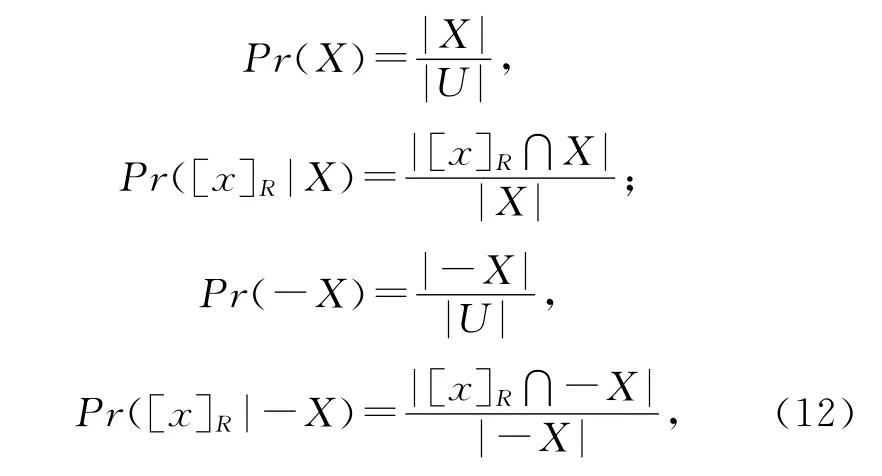
其中｜·｜表示集合中元素的个数。

Bayes理论中，条件概率Pr（X｜［x］R）可由先验概率Pr（X）和相似比计算得到，即其中，Pr（［x］R）又可以从全概率公式中计算得出：

Pr（［x］R）＝Pr（X）Pr（［x］R｜X）＋Pr（-X）Pr（［x］R｜-X），因此某类业务不违约的先验概率为

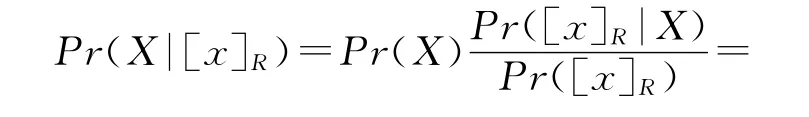
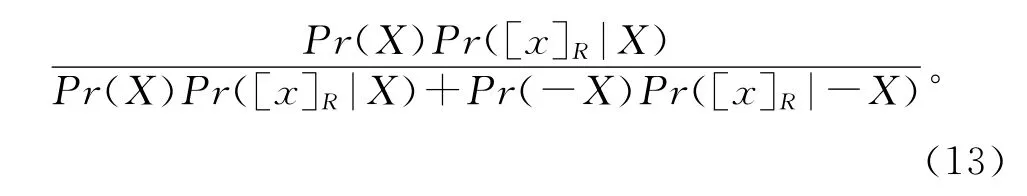
将式（12）代入式（13）中，可以求得某类业务不违约的概率值为

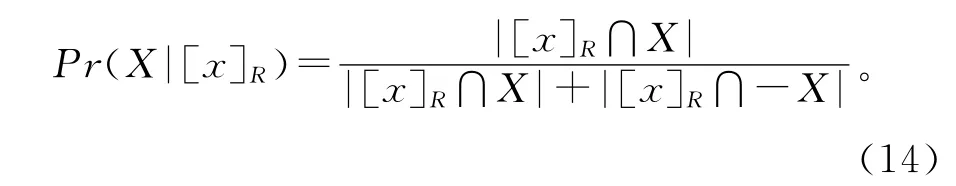
1.5 决策规则的获得

通过先验概率以及阈值的对比，可得出银行最优决策规则如下：

如果Pr（X｜［x］R）≥α，则x∈POS（X），即X发生的概率大于阈值α，银行可将这类业务划入正域，执行投资决策；

如果Pr（X｜［x］R）≤β，则x∈NEG（X），即X发生的概率小于阈值β，银行可将这类业务划分到负域中，拒绝投资该类业务；

如果β＜Pr（X｜［x］R）＜α，则x∈BND（X），即X发生的概率介于阈值α和β之间，银行可将这类业务划分到边界域中，此时决策依据不足，需要进一步考察以便作出正确决策。

2 算例分析

根据粗糙集理论，等价类是具有某些相似属性的元素的集合。针对存货质押业务，可以按照不同信用等级或者不同质物等属性划分等价类。本算例中按不同信用等级相同质物将业务划分为10个等价类（信用等级：AAA，AA，A，BBB，BB，B，CCC，CC，C，D），不同信用等级的客户在贷款时利率不同，但是由于质押物相同，因此所有等价类拥有相同的变现率，因此，作出表1所述设定。

表1 基本参数取值Tab.1 Basic parameters setting

设定若业务成功则银行出让5%的利息给物流企业。表2是10类业务的收入支出情况，在业务操作过程中，银行会根据不同信用等级设定利率，信用等级高的企业借款利率较低，而信用等级低的企业借款利率会较高，根据上节所述收支函数的确定方法，计算对于不同等价类的业务银行的收入支出。

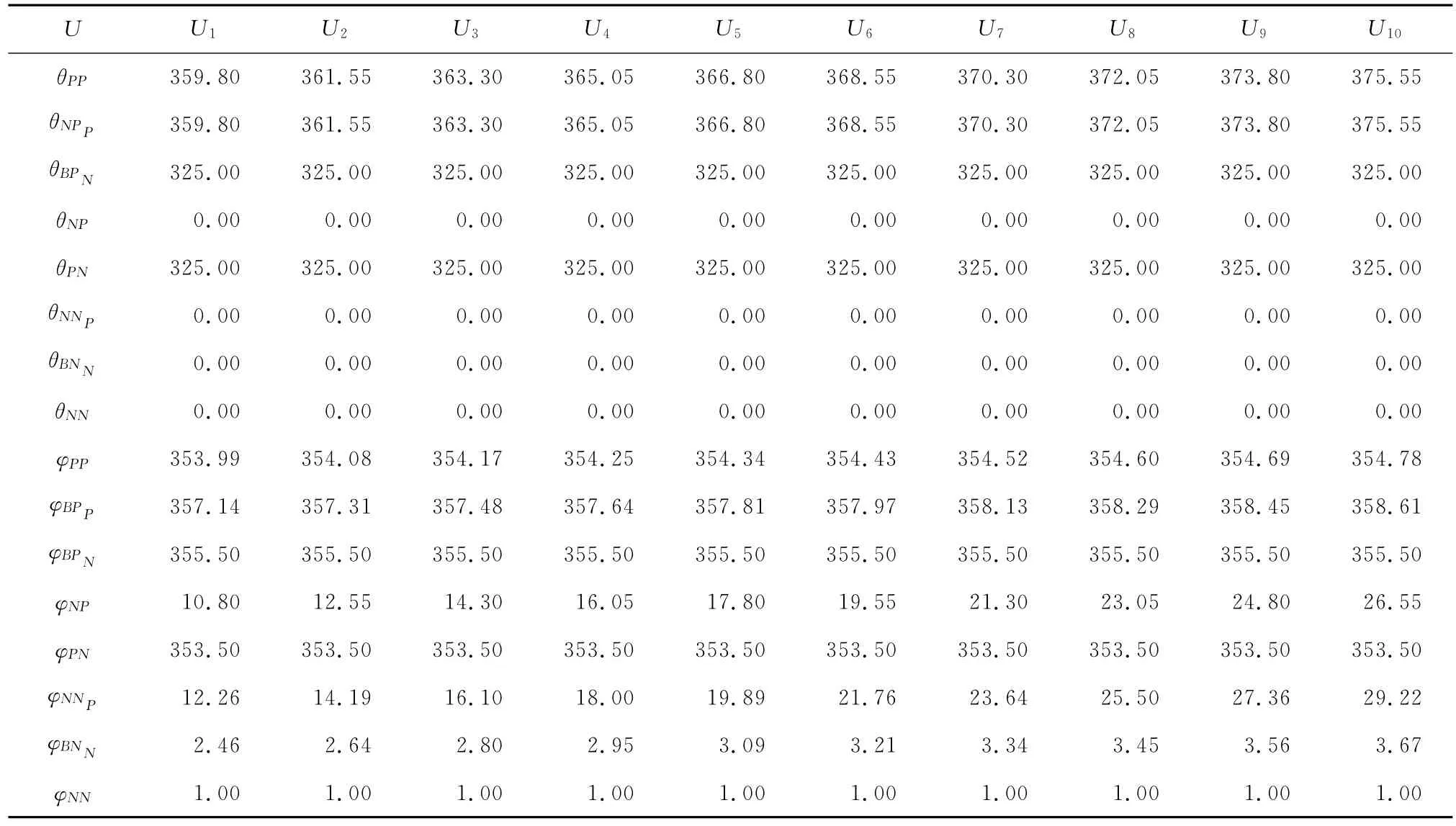
表2 不同等价类银行收入支出状况Tab.2 Balance of payments under different equivalence classes

由式（2）、式（4）、式（5）求得银行采取不同投资决策下的收入损失函数，通过式（11）求得阈值，见表3。

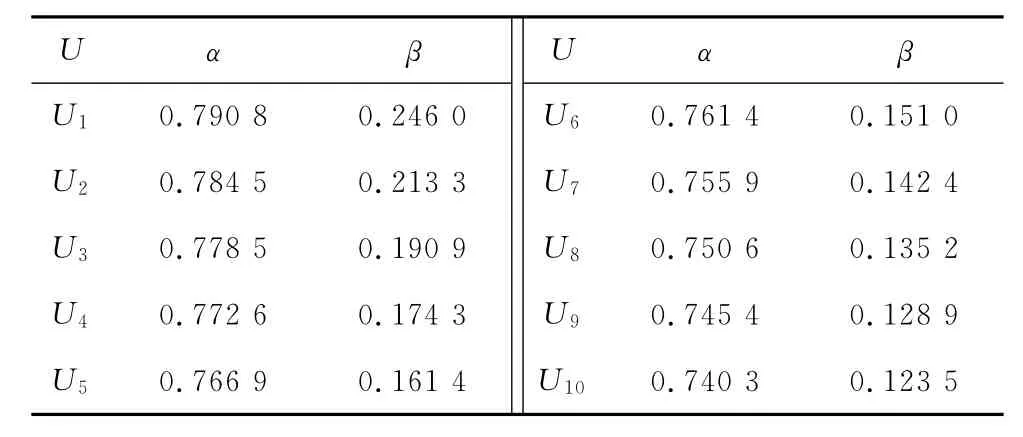
表3 不同等价类业务的阈值Tab.3 Thresholds under different equivalence classes

银行在业务操作中，积累了大量的业务信息，根据数据信息构建业务决策表，然后通过模型中计算先验概率的方法计算出Pr（X｜Ui），通过比较其与α，β的大小来作出最终决策。为了简便起见，∀Ui∈U，假设Pr（X｜Ui）＝0.77，通过决策规则，有POS（X）＝ ｛U1，U2，U3，U4｝，NEG（X）＝ ∅，BND（X）＝｛U5，U6，U7，U8，U9，U10｝。即银行对业务U1，U2，U3，U4执行投资决策，业务U5，U6，U7，U8，U9，U10可能存在违约风险，要经二次考察后决策。U1，U2，U3，U4这4个等价类的项目在收益上是较少的，因为其信用等级较高，贷款利率较低，但是同时这4类项目的违约风险较低，因此划入正域决策符合银行业务操作中“风险与收益成正比”的特点。另外，理论模型中，假设银行资金充裕，因此如果银行不投资业务，将没有任何收入，这导致银行在第1次业务筛选后，情愿付出部分考察费，继续挖掘有潜力的项目。另一方面，银行延迟决策时，计算得出了银行的最优投资考察费用值，即得出的损失函数式采取延迟决策时的最小损失，因此，算例得出的负域等于空集。

3 结 语

本文主要研究的是银行面对某一项存货质押业务时的决策问题，定量给出了投资、延迟决策、不投资业务的条件。引入“决策粗糙集”中3条决策的思想，分析银行在各种情况下的收入与支出，从而确定损失函数，通过损失函数确定阈值，从而通过和历史资料中先验概率的对比得出正确的决策。

需要指出的是，在考察投入与判断精确度函数构建方面，本文没有太多的数据来支撑假设函数。除此之外，论文仅讨论了银行主导下的单用户决策。而在实践中，存货质押业务往往是银行和物流企业联合参与下的多用户决策。因此，银行和物流企业乃至核心企业参与下的多用户决策业务决策将是下一步的研究方向。

／References：

［1］唐 雯，陈爱祖.河北中小企业发展现状与对策分析［J］.河北科技大学学报，2010，31（9）：22-27.TANG Wen，CHEN Aizu.Development status of small and medium enterprises in Hebei province and countermeasures［J］.Journal of Hebei University of Science and Technology，2010，31（9）：22-27.

［2］王千红，刘晓君.对国有商业银行创新非利息收入业务的比较分析［J］.河北科技大学学报（社会科学版），2009，9（4）：26-31.WANG Qianhong，LIU Xiaojun.Comparative analysis of the innovation of the non-interests income banking services for commercial banks of China［J］.Journal of Hebei University of Science and Technology（Social Sciences），2009，9（4）：26-31.

［3］陈祥锋，朱道立.现代物流金融服务创新——金融物流［J］.物流技术，2005（3）：4-6.CHEN Xiangfeng，ZHU Daoli.Innovation of logistics，finance service：Financing logistics［J］.Logistics Technology，2005（3）：4-6.

［4］李毅学，徐 渝，冯耕中.国内外存货质押融资业务演化过程研究［J］.经济与管理研究，2007（3）：22-26.LI Yixue，XU Yu，FENG Gengzhong.Evolution inventory financing evolution at home and abroad［J］.Research on Economics and Management，2007（3）：22-26.

［5］李毅学.供应链金融风险评估［J］.中央财经大学学报，2011（10）：36-41.LI Yixue.Risk assessment of supply chain finance［J］.Journal of Central University of Finance Economics，2011（10）：36-41.

［6］李毅学，冯耕中，徐 渝.价格随机波动下存货质押融资业务质押率研究［J］.系统工程理论与实践，2007（12）：42-48.LI Yixue，FENG Gengzhong，XU Yu.Research on loan-tovalue ratio of inventory financing under randomly-fluctuant price［J］.Systems Engineering Theory and Practice，2007（12）：42-48.

［7］李毅学，徐 渝，冯耕中，等.重随机泊松违约概率下库存商品融资业务贷款价值比率研究［J］.中国管理科学，2007，15（1）：21-26.LI Yixue，XU Yu，FENG Gengzhong，et al.On loan-to-value ratios of inventory financing with doubly stochastic poisson default processes［J］.Chinese Journal of Management Science，2007，15（1）：21-26.

［8］JOHN A B，RACHEL Q Z.Inventory management with assetbased financing［J］.Management Science，2004，50（9）：1 274-1 292.

［9］BERLING P，ROSLING K.The effects of financial risks on inventory policy［J］.Management Science，2005，51（12）：1 804-1 815.

［10］李 娟，徐 渝，冯耕中.基于存货质押融资业务的博弈分析［J］.生产力研究，2007（20）：49-50.LI Juan，XU Yu，FENG Gengzhong.Game analysis based on inventory financing business［J］.Productivity Research，2007（20）：49-50.

［11］何 娟，王 建，蒋祥林.不完全信息下存货质押业务防合谋机制设计［J］.软科学，2012（8）：141-144.HE Juan，WANG Jian，JIANG Xianglin.Mechanism design of avoiding collusion in inventory financing under incomplete information［J］.Soft Science，2012（8）：141-144.

［12］李毅学，张媛媛，汪寿阳，等.物流与供应链金融创新：存货质押融资风险管理［M］.北京：科学出版社，2010.LI Yixue，ZHANG Yuanyuan，WANG Shouyang，et al.Logistics and Supply Chain of Financial Innovation：Risk Management Inventory Financing［M］.Beijing：Science Press，2010.

［13］马中华，何 娟.物流企业参与下的存货质押融资中的委托代理问题研究［J］.中国管理科学，2008，16（10）：455-459.MA Zhonghua，HE Juan.The research of principal-agent problem in inventory finance with logistics enterprises participating［J］.Chinese Journal of Management Science，2008，16（10）：455-459.

［14］马中华，朱道立.物流企业在存货质押融资中的决策问题研究［J］.系统工程学报，2011，26（3）：346-351.MA Zhonghua，ZHU Daoli.Research of the logistics enterprises decision-making in the inventory financing［J］.Journal of Systems Engineering，2011，26（3）：346-351.

［15］YAO Y Y，WONG S K M，LINGRAS P.A decision-theoretic rough set model［A］.Proceedings of the 5th International Symposium on Methodologies for Intelligent Systems［C］.［S.l.］：［s.n.］，1990.386-392.

［16］LIU D，LI H X，ZHOU X Z.Two decades research on decision-theoretic rough set［A］.Proceeding of 9thIEEE International Conference on Cognitive Informatics［C］.［S.l.］：［s.n.］，2010.731-739.

［17］刘 盾，姚一豫，李天瑞.三支决策粗糙集［J］.计算机科学，2010，38（1）：245-250.LIU Dun，YAO Yiyu，LI Tianrui.Three-way decision-theoretic rough sets［J］.Computer Science，2010，38（1）：245-250.

［18］李华雄，刘 盾，周献中.决策粗糙集模型研究综述［J］.重庆邮电大学学报（自然科学版），2010，22（5）：624-630.LI Huaxiong，LIU Dun，ZHOU Xianzhong.Rewiew on decision-theoretic rough set model［J］.Journal of Chongqing University of Posts and Telecommunications（Natural Science），2010，22（5）：624-630.

［19］李华雄，周献中，李天瑞，等.决策粗糙集理论及其研究进展［M］.北京：科学出版社，2011.LI Huaxiong，ZHOU Xianzhong，LI Tianrui，et al.Decision-Theoretic Rough Set and Its Research Progress［M］.Beijing：Science Press，2011.