不锈钢制内压短圆筒的承载能力
2013-10-09吴元祥张红卫袁小会刘小宁
吴元祥,刘 兵,张红卫,刘 岑,袁小会,刘小宁,
(1.武汉软件工程职业学院机械制造工程系,湖北武汉 430205;2.武汉工程大学机电工程学院,湖北武汉 430074)
屈服和爆破强度是钢制薄壁内压圆筒承载能力的表征,承载能力受到封头加强和提高的钢制薄壁内压圆筒称为内压短圆筒。对于用低碳钢、不锈钢和ABS等材料制造的钢制薄壁内压短圆筒,研究表明[1-8],其屈服或爆破强度与长径比及封头结构有关,用中径公式[9]计算有较大的误差。由于0Cr13不锈钢制薄壁内压短圆筒是食品和医药等行业常用的特种设备,因此,文中基于试验数据,研究了标准椭圆封头与碟形封头对0Cr13不锈钢制薄壁短圆筒屈服和爆破强度加强程度和加强范围的影响。
1 建立模型
短圆筒承载能力的经验公式形式为[1-6]
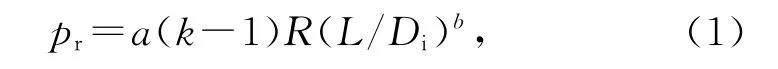
式中:pr为短圆筒的承载能力;k为圆筒内外径比,k=1+2δ/Di;δ为圆筒壁厚;Di为圆筒内直径;L为筒体长度;a,b为经验系数,由试验数据确定。
当R分别取圆筒材料的屈服与抗拉应力ReL与Rm时,pr分别为短圆筒的屈服与爆破压力ps与pb。
由式(1)可得:
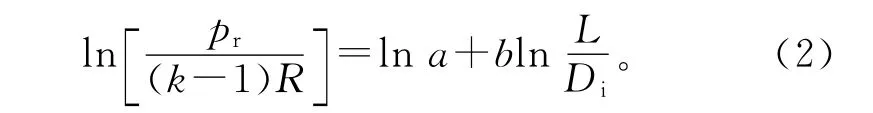
对于n组短圆筒屈服与爆破的试验数据,令:

由试验测量pr,δ,L与Di,可得xi与yi的均值:

根据最小二乘法线性回归分析,可得经验数据a,b和相关度r:

区分内压长、短圆筒的临界长度计算公式:

式中,Lcrr为薄壁内压长、短圆筒的临界长度。
屈服与爆破失效准则的Lcrr分别为Lcrs与Lcrb。由式(8)可知,当L>Lcrr时为薄壁内压长圆筒,当L=Lcrr时为薄壁内压临界圆筒,当L≤Lcrr时为薄壁内压短圆筒。
2 试验数据
文献[1]采用0Cr13不锈钢制薄壁内压圆筒容器进行常温水压试验,材料0Cr13的屈服与抗拉应力分别为222MPa与450MPa。试验圆筒由单层圆筒与标准椭圆封头或碟形封头组成,封头厚度为δ1,标准椭圆封头圆筒的编号为S,椭圆封头直边高度为hi;碟形封头圆筒的编号为D,其过渡段半径为r。试验圆筒的结构尺寸与试验数据见表1。

表1 0Cr13不锈钢制薄壁内压短圆筒屈服和爆破强度试验数据[1]Tab.1 Test data of yield and burst strength of 0Cr13steel short steel thin-wall internal pressure cylinder[1]
3 承载能力分析
3.1 相同结构封头短圆筒承载能力
将表1中的S1-S7,D1-D7作为薄壁内压短圆筒试验数据,代入式(1)-式(8)中可得a,b,r,即得到计算相同结构封头短圆筒承载能力的公式。
3.1.1 短圆筒与标准椭圆封头的承载能力
1)爆破强度与临界长度
a=1.216 3,b=-0.335 4,r=-0.970 6,
即

式中,pb1为采用标准椭圆封头短圆筒的爆破强度。
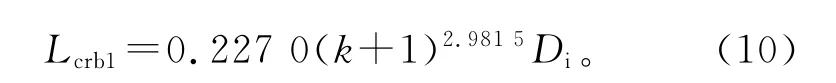
式中,Lcrb1为采用标准椭圆封头的短圆筒在爆破失效准则下的临界长度。
2)屈服强度与临界长度

即

式中,ps1为采用标准椭圆封头短圆筒的屈服强度。
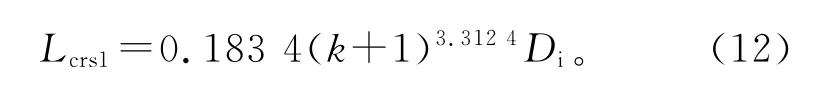
式中,Lcrs1为采用标准椭圆封头的短圆筒在屈服失效准则下的临界长度。
因为k≥1.004,由式(12)可得最小临界长径比Lcrs1/Di=1.834,基于屈服失效准则,采用标准椭圆封头的0Cr13不锈钢制薄壁内压圆筒,在L/Di≤1.834时是短圆筒。
3)标准椭圆封头对短圆筒承载能力的加强范围
由式(10)与式(12)得,Lcrb1/Lcrs1=1.238(k+1)-0.3309,因1.004≤k≤1.50[9],故 有0.914≤Lcrb1/Lcrs1≤0.984,因此,标准椭圆封头对短圆筒屈服强度的加强范围比爆破强度的宽。
3.1.2 碟形封头短圆筒的承载能力
空间:家具的中间,尤其是柜体中间是否有封闭空间,避免儿童躲藏在其中。如果有,该空间应配有通风口,以免孩子在里面窒息。
1)爆破强度与临界长度

即
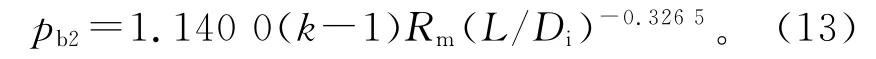
式中,pb2为采用碟形封头短圆筒的爆破强度。

式中,Lcrb2为采用碟形封头的短圆筒在爆破失效准则下的临界长度。
由k≥1.004与式(14)可得最小临界长径比Lcrb2/Di=1.503,基于爆破失效准则,采用碟形封头的0Cr13不锈钢制薄壁内压圆筒,在L/Di≤1.503时是短圆筒。
2)屈服强度与临界长度

即

式中,ps2为采用碟形封头短圆筒的屈服强度。
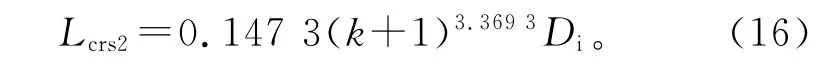
式中,Lcrs2为采用碟形封头的短圆筒在屈服失效准则下的临界长度。
由k≥1.004与式(16)得最小临界长径比Lcrs2/Di=1.532,基于屈服失效准则,采用碟形封头的0Cr13不锈钢制薄壁内压圆筒,在L/Di≤1.532时是短圆筒。
3)碟形封头对短圆筒承载能力的加强范围
由式(12)与式(14)得Lcrb2/Lcrs2=1.214(k+1)-0.3065,由于1.004≤k≤1.50,故有0.917≤Lcrb2/Lcrs2≤0.981,因此,碟形封头对薄壁内压短圆筒屈服强度的加强范围比爆破强度的宽。
根据以上分析可知,表1是0Cr13不锈钢制薄壁内压短圆筒的试验数据。
3.2 不同结构封头对短圆筒承载能力的影响
在制造材料与圆筒径比相同的条件下,可比较标准椭圆封头与碟形封头对薄壁内压短圆筒爆破与屈服强度的加强程度与范围的影响。
3.2.1 在屈服失效准则下的加强程度与范围
由式(15)与式 (11)得ps2/ps1=0.945 (L/Di)0.0051,因为短圆筒的常用长径比范围为0.5≤L/Di≤1.50,所以有0.942≤ps2/ps1≤0.947,表明碟形封头对内压短圆筒屈服强度的加强程度比标准椭圆封头的小。
由式(16)与式(12)得Lcrs2/Lcrs1=0.803(k+1)0.0569,因为1.004≤k≤1.50,所以有0.835≤Lcrs2/Lcrs1≤0.846,表明碟形封头对薄壁内压短圆筒屈服强度的加强范围比标准椭圆封头的窄。
3.2.2 在爆破失效准则下的加强程度与范围
由式 (13)与 式 (9)得pb2/pb1=0.822(L/Di)0.0089,由于0.5≤L/Di≤1.50,所以有0.817≤pb2/pb1≤0.825,表明碟形封头对薄壁内压短圆筒爆破强度的加强程度比标准椭圆封头的小。
由式(14)与式(10)得Lcrb2/Lcrb1=0.787(k+1)0.0831,因为1.004≤k≤1.50,所以0.834≤Lcrb2/Lcrb1≤0.849,表明碟形封头对薄壁内压短圆筒爆破强度的加强范围比标准椭圆封头的窄。
4 结 论
1)当0Cr13不锈钢制薄壁内压短圆筒采用标准椭圆封头或者采用碟形封头时,基于试验数据,建立了计算其屈服和爆破强度的经验公式,得到区分内压长、短圆筒的临界长度计算公式。
2)0Cr13不锈钢制标准椭圆封头薄壁内压圆筒,在屈服失效准则下,长径比不大于1.834的为短圆筒;在爆破失效准则下,长径比不大于1.804的为短圆筒;标准椭圆封头对短圆筒屈服强度的加强范围比爆破强度的宽。
3)0Cr13不锈钢制碟形封头薄壁内压圆筒,在屈服失效准则下,长径比不大于1.532的为短圆筒;在爆破失效准则下,长径比不大于1.503的为短圆筒;碟形封头对短圆筒屈服强度的加强范围比爆破强度的宽。
4)在制造材料与圆筒径比相同的条件下,碟形封头对0Cr13不锈钢制薄壁内压短圆筒屈服和爆破强度的加强程度比采用标准椭圆封头的小,加强范围也比采用标准椭圆封头的窄。
/References:
[1]张红卫,韩春鸣,刘 岑,等.0Cr13不锈钢制薄壁内压短圆筒的静强度[J].化工机械,2011,38(6):717-720.ZHANG Hongwei,HAN Chunming,LIU Cen,et al.Static intensity of 0Cr13stainless steel thin-wall short cylinder with intrinsic pressure[J].Chemical Engineering Machinery,2011,38(6):717-720.
[2]刘小宁,张红卫,刘 岑,等.钢制薄壁内压短圆筒静强度的试验研究[J].压力容器,2009,26(7):11-14.LIU Xiaoning,ZHANG Hongwei,LIU Cen,et al.Test research on static strength of steel thin-wall short cylinder at internal pressure[J].Pressure Vessel Technology,2009,26(7):11-14.
[3]张红卫,刘 岑,吴元祥,等.碟形封头对薄壁内压短圆筒爆破压力的影响[J].工业安全与环保,2011,37(4):31-32.ZHANG Hongwei,LIU Cen,WU Yuanxiang,et al.Influence of small dish shape shell cover on thin wall intrinsic pressure short cylinder burst pressure[J].Industrial Safety and Environmental Protection,2011,37(4):31-32.
[4]周 波,於孝春.标准椭圆形封头爆破压力的计算[J].工业安全与环保,2010,36(9):43-45.ZHOU Bo,YU Xiaochun.Calculation of the burst pressure of standard ellipsoidal head[J].Industrial Safety and Environ-mental Protection,2010,36(9):43-45.
[5]张红卫,刘 岑,陈 刚,等.确定短ABS塑料圆管爆破压力的经验公式[J].化肥设计,2010,48(5):18-19.ZHANG Hongwei,LIU Cen,CHEN Gang,et al.Empirical formula for determining burst pressure of short ABS plastic circular pipe[J].Chemical Fertilizer Design,2010,48 (5):18-19.
[6]刘小宁,张红卫,潘传九,等.液化石油气钢瓶承载能力的研究[J].工业安全与环保,2011,37(11):9-11.LIU Xiaoning,ZHANG Hongwei,PAN Chuanjiu,et al.Research on bearing capacity of liquified petroleum gas cylinders[J].Industrial Safety and Environmental Protection,2011,37(11):9-11.
[7]邓阳春,陈 钢,杨笑峰.简单结构平面应力等比例加载塑性失稳研究[J].机械强度,2010,32(4):675-680.DENG Yangchun,CHEN Gang,YANG Xiaofeng.Study on plastic instability of simple structures in plane stress under proportional loading[J].Journal of Mechanical Strength,2010,32(4):675-680.
[8]马 利,郑津洋,寿比南,等.奥氏体不锈钢制压力容器强度裕度研究[J].压力容器,2008,25(1):1-5.MA Li,ZHENG Jinyang,SHOU Binan,et al.Strength margin analysis for austenitic stainless steel pressure vessels[J].Pressure Vessel Technology,2008,25(1):1-5.
[9]GB 150—2011,压力容器[S].GB 150—2011,Pressure Vessel[S].
[10]丁伯民,黄正林.化工容器[M].北京:化学工业出版社,2003.DING Bomin,HUANG Zhenglin.Chemical Vessel[M].Beijing:Chemical Industry Press,2003.
