基于层次分析法的信息系统安全评价研究

刘仁山，孟祥宏

（呼伦贝尔学院计算机科学与技术学院，内蒙古呼伦贝尔 021008）

随着计算机网络的普及和信息系统的广泛应用，安全问题面临着严峻的挑战，成为信息化建设亟需解决的重要前沿课题。信息化是信息系统与社会系统相互作用的一个综合发展进程，涉及的不仅仅是计算机技术，还包括人的操作、管理行为等。所以产生的安全问题和系统问题相互制约，使得信息安全具有很大的综合性、复杂性和不确定性［1-2］。同时，信息安全保护会伴随信息化的发展而不断变化。为了更好地保护信息安全，迫切需要针对不同部门信息系统研究建立科学的、可度量的、可操作的信息安全保护评价指标体系［1-2］。

对信息系统的安全性进行科学合理的评价是一个复杂的系统问题，是对信息系统进行安全建设和有关部门进行科学决策的重要依据。不同的系统对于安全的需求是不一样的，比如金融、军事等部门对于系统的安全性要求很高，而销售、教育等部门对于系统的安全需求程度就较低，因此对系统进行科学评价有利于发现系统安全状况与相应等级要求的差距，有针对性地对系统采取相应的防范措施，提高系统的安全能力。

信息系统保护不仅涉及技术而且还包括管理，而技术和管理又可细分为许多小指标，因此，科学合理地建立评价指标体系是信息系统评价的基础。同时，不同评价指标之间相互关联、重要程度也各不相同，主要体现在评价指标的权重上，权重反映了评价体系中各个指标在系统安全中的地位，如何确定评价指标的权重将直接影响评价的客观性与真实性。

对系统的安全状况进行综合评价必须采用系统工程的思想和方法，中国有关安全评价方法的研究虽然很多，但尚无全面的综合评价指标体系和成形的安全评价数学模型，而且在实际应用中普遍存在定量、定性分析不足的问题，因此笔者采用层次分析法（AHP）进行信息系统的安全评估。层次分析法是美国运筹学家SAATY在1977年提出的一种定性与定量相结合的决策分析方法，将递阶层次、分级综合、逻辑判断综合起来，使人们的思维决策趋于条理和有效，其特点很适合于信息安全的综合评价。根据系统安全的需求建立评价指标体系，通过AHP法建立判断矩阵，利用向量范数法校正判断矩阵的不一致性，科学计算评价指标的权重，使安全评估更加科学、客观。

1 构建安全指标评价体系

1.1 建立层次结构模型

依据《信息安全管理实用规则》（ISO／IEC 27002）和信息技术安全通用要求（GJB 5095-2002），将信息系统安全划分为信息安全、硬件安全、软件安全、管理安全和环境安全5个层面。同时针对信息系统安全风险评估的特点，结合指标体系建立的一般原则，利用德尔菲法对这5个层面进行指标分解，建立了信息系统安全评估指标体系［3-6］，其层次结构模型如图1所示，信息系统安全是目标层（A），准则层（B）由信息安全、软件安全、硬件安全、管理安全和环境安全5部分组成，指标层（C）包括身份鉴别、访问控制、信息加密等21项指标。

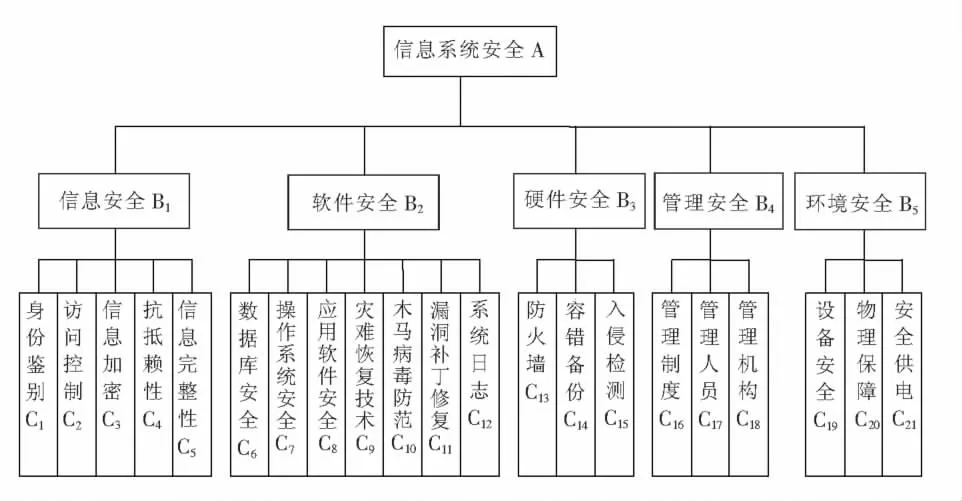
图1 信息系统安全评价指标体系Fig.1 Information system security evaluation index system

1.2 判断矩阵的基本理论

判断矩阵是AHP的出发点。如何构造判断矩阵是AHP的关键一步。判断矩阵表示针对上一层某元素，本层次有关元素之间相对重要性，假定A层中元素Ak与下一层中元素B1，B2，…，Bn有联系，构造的判断矩阵取下面的形式：

其中，bij表示相对于Ak而言，Bi和Bj相对重要性的数值表现形式，通常bij取1，3，…，9及它们的倒数，其含义如表1所示［8］。

判断矩阵具有如下性质：

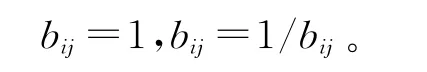
由于判断矩阵具有上述性质，称为正的互反矩阵。构造判断矩阵时，仅需对其上（下）三角元素给出n（n-1）／2个判断。

表1 判断矩阵含义Tab.1 Judgment matrix meaning

由于人们对于复杂事物的各因素进行两两比较时，判断不可能完全一致，所以在计算之前，要先检验判断矩阵的逻辑一致性，以CR＝CI／RI作为判断矩阵一致性的指标，式中作为判断矩阵随机一致性的指标，n为判断矩阵的维数，RI为平均随机一致性比例，3～10阶矩阵的RI取值见表2。一般来说，CR越小，判断矩阵的一致性越好。当CR≤0.1时，即认为判断矩阵具有令人满意的一致性，否则，必须重新进行两两比较判断，并使之具有满意的一致性。

表2 平均随机一致性Tab.2 Aaverage random consistency

1.3 基于向量范数法的判断矩阵不一致性的校正

1.3.1 向量范数法的基本理论

由于客观因素的复杂性、不确定性，利用层次分析法构造判断矩阵时很难对因素相对重要性程度作出精确判断，这样就导致了构造的判断矩阵不能通过一致性检验，此时就应当对原来的判断矩阵进行校正［9］，为了克服重新调整过程中的主观性和盲目性，笔者采用基于向量范数的校正方法。

定义 设n维向量X＝ （x1，x2，…，xn）T，Y＝（y1，y2，…，yn）T，则称X-Y＝ （x1-y1，…，x1-yn）T为向量X与向量Y的差向量，同时‖X-Y‖＝为差向量的范数。

设A＝ （aij）＝ （a1，a2，…，an）为一判断矩阵，为A各列归一化后的矩阵，则矩阵归一化特征向量

若A完全一致，则

若A不完全一致，则这时，用差向量的范数来度量之间的关系，且把W近似地设为均向量，用di表示差向量范数的变化。

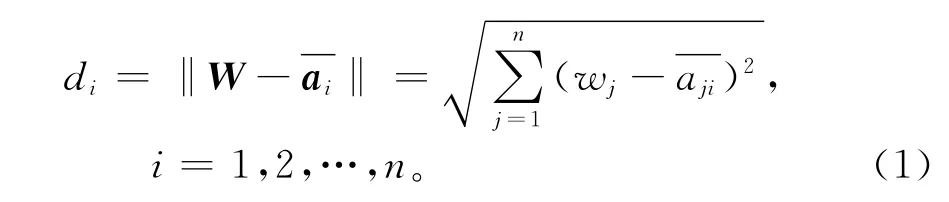
显然，当A完全一致时，di＝0，i＝1，2，…，n，当A不完全一致时，di不等于0，且有di越大，表示与W的偏差越大，di越小，表示与W的偏差越小。对di进行排序，假设有di1＜di2＜…＜din-1＜din，当判断矩阵一致性不好时，应首先调整偏差最大的2个din-1和din对应的两例关系，若设in-1和in分别对应原来的矩阵的第i列和第j列，则只需校正aij和aji，在矩阵A中有［8］

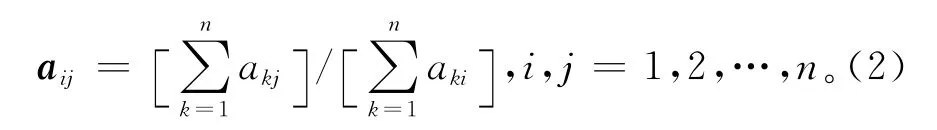
这样，可以用式（2）对需要校正的aij和aji进行重新计算，若判断矩阵仍旧不一致，则进行微调。

1.3.2 基于向量范数法的判断矩阵不一致性修正流程

利用层次分析法对信息系统的安全评价指标进行权重计算，必须构造合理的、满足一致性要求的判断矩阵，判断矩阵是利用专家知识对指标层的评价指标相对于准则层中某个元素的相对重要性进行两两比较，全部指标经过专家的两两判定之后形成的，如果判断矩阵没有满足一致性要求，则必须调整判断矩阵中评价指标的标度，采用向量范数方法能够科学、快速地校正判断矩阵，其工作流程如图2所示。

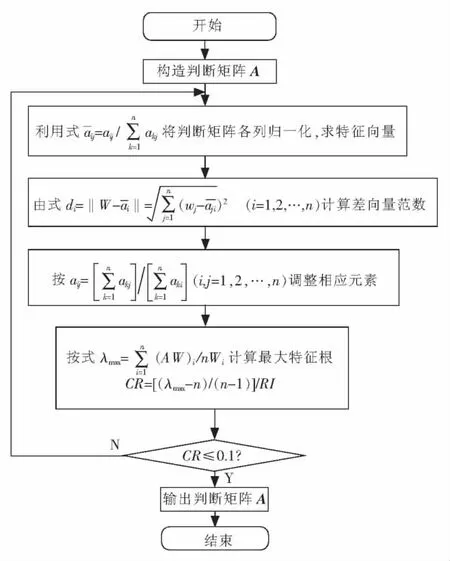
图2 判断矩阵的校正流程Fig.2 Judgment matrix correction flowchart

1.3.3 信息安全评价指标权重的计算

根据图1和图2，对信息系统安全评价的准则层得出的判断矩阵为

对数据安全的指标层得出的判断矩阵为

对软件安全的指标层得出的判断矩阵为

利用数学工具软件Matlab对判断矩阵进行归一化运算，求得A，B1，B23个矩阵排序权重向量为

MA= ［0.511 2，0.265 0，0.134 4，0.067 0，0.034 6］T，

MB1＝ ［0.368 5，0.206 4，0.206 4，0.109 4，0.109 4］T，

MB2＝ ［0.398 0，0.196 3，0.196 3，0.095 5，0.045 1，0.045 1，0.023 8］T，

由MA可以求得矩阵A的最大特征值λmax＝5.239 5，CI＝ （5.239 5-5）／4＝0.059 86，查表知RI＝1.12，则CR＝CI／RI＝0.053 45＜0.1，判断矩阵具有很好的一致性，同理矩阵B1和B2的CI值分别是0.088 56和0.035 9，矩阵均满足一致性要求。

按照上面的算法可以求得：

硬件安全判断矩阵B3的排序权重向量为

MB3= ［0.430 2，0.354 3，0.215 5］T；

管理安全判断矩阵B4的排序权重向量为

MB4＝ ［0.412 6，0.327 5，0.259 9］T；

环境安全判断矩阵B5的排序权重向量为

MB5＝ ［0.383 3，0.333 4，0.283 3］T。

已知准则层对目标层的权重MA、指标层对准则层的权重MB。利用如下公式：

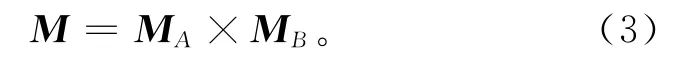
计算得综合权重向量，如表3所示。

表3 综合评价权重Tab.3 Proportional weight values

2 综合实例分析

求得信息安全评价指标的综合权重后就可以对信息系统的安全性进行评估，信息系统安全的评价等级分为A，B，C，D，E共5个等级，分别对应信息系统安全程度很安全、安全、一般、较低、危险，本模型总分为100分，安全等级及对应分值如表4所示。

表4 信息系统安全等级及对应分值Tab.4 Security level of information system and its value

请专家对指标层的各项指标进行打分，然后对各单项指标进行加权综合，计算公式为

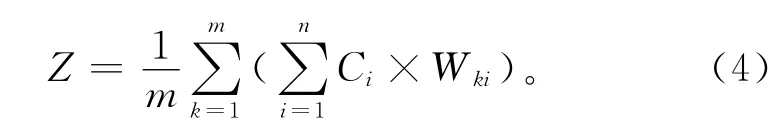
式中：m为专家人数，n为指标层单项指标数量，Ci为第i个指标的权重值，Wki为第k个专家给第i指标的打分值。所得综合分值越高说明信息系统安全等级越高，反之，分值越低，信息安全等级越低。

采用这种方法对校园OA系统进行综合分析评价，经计算，综合得分值为84.12，安全等级为B级，安全程度较高，同时对21个指标的得分进行分析后发现，硬件安全程度最好而信息安全则较差，从而为网络安全管理提供科学指导。这种评价方法比传统评价减少了评价过程中人为主观因素的影响，有助于发现网络安全中存在的具体问题。

3 结 语

从信息系统安全评价的实际需要入手，构建了科学合理的安全指标评价体系，并在层次分析法的基础上建立了综合分析评价模型，采用向量范数法解决构造矩阵调整的复杂性问题，提高了评价模型的可用程度，层次分析法减少了评价过程中主观因素的影响，有利于进行科学的安全测评，提高用户对系统整体安全防护能力的了解，采用符合系统自身需要的安全策略，提高信息系统整体安全水平和收益。

／References：

［1］郭锡泉，姚国祥.网络安全管理的多维度可拓模糊综合评价［J］.计算机工程，2011，37（4）：287-290.GUO Xiquan，YAO Guoxiang.Multi-dimensional extensionfuzzy comprehensive evaluation［J］.Computer Engineering，2011，37（4）：287-290.

［2］陈艳春.Mashup应用安全风险评估模型研究［J］.河北科技大学学报，2011，32（1）：161-164.CHEN Yanchun.Security risk evaluation model for Mashup application［J］.Journal of Hebei University of Science and Technology，2011，32（1）：161-164.

［3］张 利，姚轶崭，彭建芬，等.基于决策树的智能信息安全风险评估方法［J］.清华大学学报（自然科学版），2011，57（10）：1 236-1 239.ZHANG Li，YAO Yizhan，PENG Jianfen，et al.Intelligent information security risk assessment based on a decision tree algorithm［J］.Journal Tsinghua University（Science and Technology），2011，57（10）：1 236-1 239.

［4］陈朝阳，路文杰，俞会新.基于群体AHP方法的销售团队凝聚力分析［J］.河北科技大学学报，2009，30（3）：271-274.CHEN Zhaoyang，LU Wenjie，YU Huixin.Analysis of sales team cohesion based on group AHP［J］.Journal of Hebei University of Science and Technology，2009，30（3）：271-274.

［5］许 敏，宋亚欣.基于层次分析法的知识型员工绩效考核体系设计［J］.河北科技大学学报，2009，30（4）：365-369.XU Min，SONG Yaxin.Performance evaluation system for knowledgeable workers based on analytic hierarchy process［J］.Journal of Hebei University of Science and Technology，2009，30（4）：365-369.

［6］许福永，申 健，李剑英.网络安全综合评价方法的研究及应用［J］.计算机工程与设计，2006，27（8）：1 398-1 400.XU Fuyong，SHEN Jian，LI Jianying.Study and application of comprehensive assessment method for network security［J］.Computer Engineering and Design，2006，27（8）：1 398-1 400.

［7］李健宏，李广振.网络安全综合评价方法的应用研究［J］.计算机仿真，2011，28（7）：165-168.LI Jianhong，LI Guangzheng.Application study on evaluation method of network security［J］.Computer Simulation，2011，28（7）：165-168.

［8］姜启源.数学模型［M］.北京：高等教育出版社，2003.JIANG Qiyuan.Mathematical Model［M］.Beijing：Higher Education Press，2003.

［9］杨 萍.关于AHP中判断矩阵校正方法的新探索［J］.工科数学，2001（4）：23-25.YANG Ping.The new study on rectification method for the judgement matrix in AHP［J］.Journal of Mathematics for Technology，2001（4）：23-25.

［10］石金波，李庆波.高校后勤满意度测评系统的体系设计及其实现［J］.河北工业科技，2012，29（4）：246-249.SHI Jinbo，LI Qingbo.Design and implementation of satisfaction assessment system for college logistics［J］.Hebei Journal of Industrial Science and Technology，2012，29（4）：246-249.