利用Radon－Wigner变换的LFM信号检测性能分析

许建忠，孙红伟，孙业岐，段平光，陈刚

（1.河北大学物理科学与技术学院，河北保定 071002；2.河北大学工商学院，河北保定 071002；3.北华航天工业学院，河北廊坊 065000）

线性调频（linear frequency modulation，LFM）信号是一种重要的信号形式，在雷达、通信和地震勘测等系统中都有着广泛的应用，对LFM信号的检测和参数估计一直是研究的重点和难点.国内外学者对LFM信号的检测已经提出了很多有效的方法，如基于最大似然的方法［1］，基于STFT 及其他时频分析的检测方法等［2］.Wigner－Ville分布（Wigner－Ville distribution，WVD）是最早用于对LFM信号进行时频分析的方法之一，Simon［3］在强杂波背景下应用WVD检测雷达目标，优于普通的恒虚警检测方法，Frazer［4］将WVD应用于HF超视距雷达，提高了HF超视距雷达的检测性能.但是当用WVD分析多分量LFM信号时，由于WVD存在固有的交叉项，对检测结果造成影响［5］.LFM信号在分数阶Fourier变换（Fractional Fourier transform，FRFT）域有良好的能量聚集性，因此在FRFT域处理LFM信号的检测与估计问题有很大的优势.但在低信噪比时，FRFT对噪声的抑制作用有限，检测性能降低，并且多分量LFM信号的FRFT谱存在相互遮蔽问题［6］，影响了对弱信号的检测.

LFM信号经过Wigner－Ville变换后在时频平面内表现为冲激线谱，因此在Wigner－Ville变换的基础上应用Radon变换，形成Radon－Wigner变换（Radon－Wigner transform，RWT），可以利用信号项的能量聚集，有效实现对信号的检测.本文分析了采用RWT进行LFM信号检测的方法和性能，给出了检测的信噪比和检测概率.仿真实验验证了该方法的有效性.

1 Radon－Wigner变换

连续解析信号x（t）的WVD为［7］

WVD对线性调频信号具有很好的时频聚集性，但在分析多个信号时，在信号之间、噪声之间、信号和噪声之间存在着严重的交叉项，影响了对有用信号的检测.RWT是对信号的WVD进行直线积分投影的Radon变换，通过Radon变换对WVD平面进行积分可以实现对信号项的聚集和对交叉项的平滑，在一定程度上能够抑制交叉项的影响.

将时频平面坐标逆时针旋转α角得到新的坐标（u，v），以不同的u值平行于v轴积分，即得到Radon变换，如图1所示为RWT的几何示意图，坐标间的变换关系为

若将时频平面代之以信号x（t）的WVD，即得到x（t）的RWT

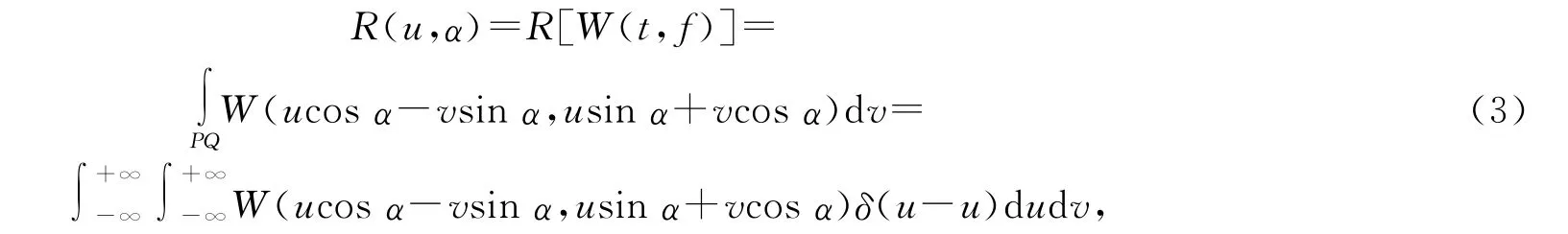
式中R［·］表示Radon变换.

图1 Radon变换几何示意Fig.1 Geometric forms of Radon transformation

在WVD时频平面中，若用f轴的f0和斜率β为参数来表示直线，则当沿f＝f0＋βt作直线积分时，可将图1中的积分路径参数（u，α）替换为（f0，β），根据图中2对参数之间的关系，可以得到用（f0，β）表示的RWT

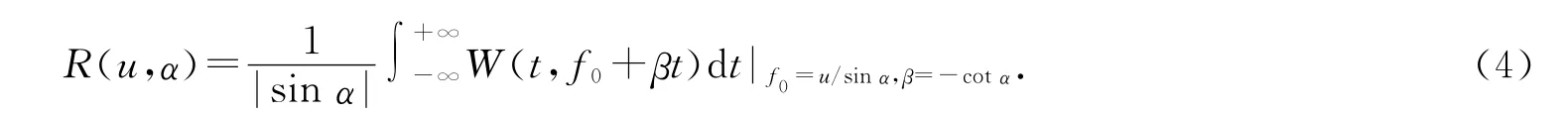
上式表明，若x（t）是起始频率为f0和调频斜率为β的LFM信号，则积分值最大；而当参数偏离f0，β时积分值迅速减小；因而对一定的LFM信号其RWT会在对应的参数（f0，β）处呈现尖峰.由此，在RWT域中可容易地将信号与交叉项区分开.

2 基于Radon－Wigner变换的检测分析

由RWT的定义可知，RWT是通过对信号WVD平面（t，f）应用Radon变换进行投影积分，利用LFM信号在时频平面上的能量聚集特征，以实现信号的检测.

2.1 检测信噪比

对于回波信号

其中s（t）为真实的目标回波信号成分，w（t）为噪声或杂波干扰.假设LFM信号的离散化表达式为

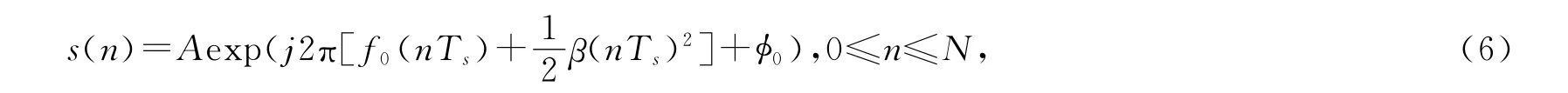
其中Ts为采样周期，N为采样个数，φ0为初始相位.

若只有信号s（n）而不存在噪声时，则R（u，α）在（u，α）参数空间内呈现为一尖峰，其峰值位于参数（f0，β）对应的（u0，α0）处，峰值为N2A2／2，而对于有噪声的观测信号x（n）则在（u0，α0）处会发生随机起伏，并有一定的起伏方差var｛R（u，α）｝，Barbarossa［8］提出把二维变换域上的信号峰值平方作为信号功率，该处的噪声方差作为噪声功率，因此可以得到基于RWT的信噪比

分母项var｛R（u，α）｝的计算可分2步进行［7］，首先计算其数学期望

这里假设了杂噪信号的自相关函数Rw（k）＝，然后计算含杂噪信号RWT的二阶矩

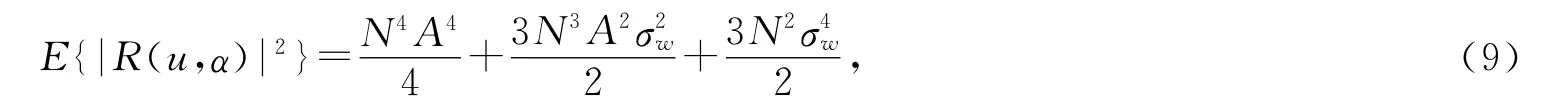
因此，由式（8），（9）可以得到含杂噪信号的方差

综合式（7），（10），最终可得含杂噪信号的RWT输出信噪比为

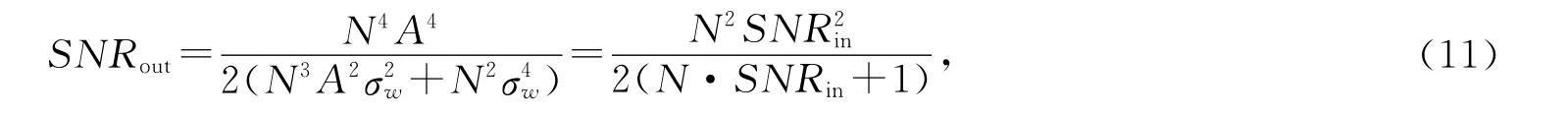
其中SNRin＝为输入信噪比，并由式可见增大数据长度N是改善信噪比的一个有效手段.

2.2 检测概率分析

对目标检测，构造二元假设检验［9］

式中x（t），s（t，ρ），w（t）分别代表接收信号、目标回波信号、噪声和杂波干扰等.ρ为目标中的未知参数，对于LFM信号来说，ρ＝［f0β］.

在u，α参数空间内，设Xu，α为接收信号经RWT后在（u，α）点的值，若检测门限为λ，则其虚警概率为

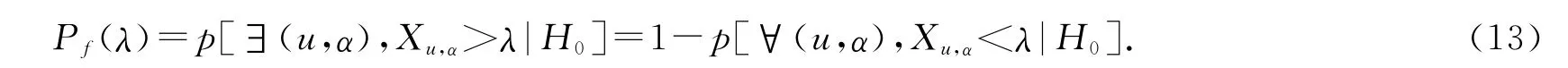
同样有其检测概率

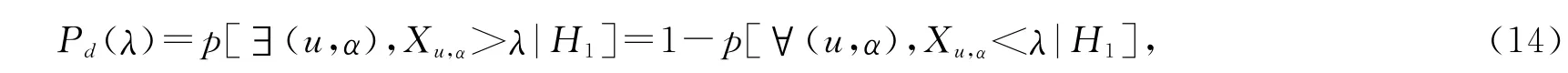
式中∃（u，α）表示存在（u，α）点，∀（u，α）表示对任意存在的（u，α）点.

假设经RWT后信号中的噪声为高斯白噪声，则由式（8），（10）可知在无目标信号时的噪声概率密度函数为

同理，可以得到有目标信号时的噪声概率密度函数

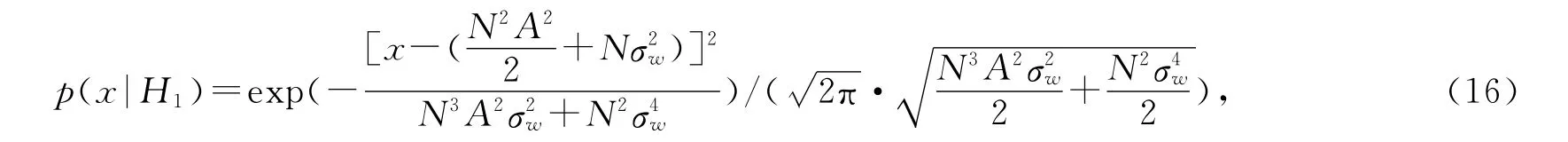
因此，由式（15）可以得到虚警概率为

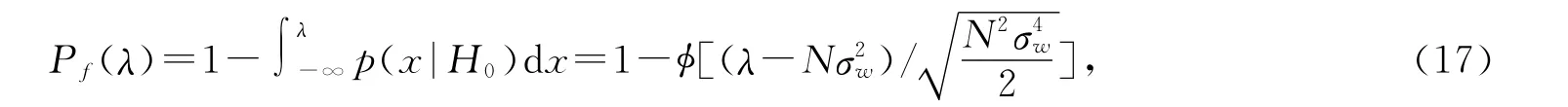
式中φ（x）称为概率积分函数，其定义为

由式（16）可以得到目标的检测概率

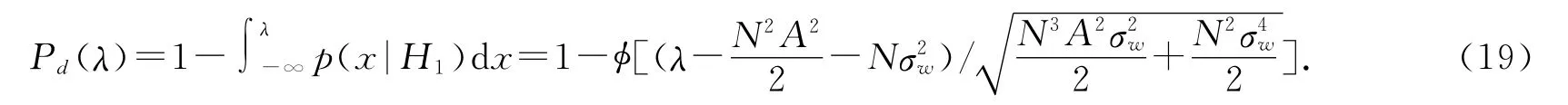
这样，通过式（17）可以得到给定虚警概率Pf情况下的门限值λ，由式（19）就可以得到在一定门限下的检测概率Pd.

3 仿真结果与分析

3.1 噪声干扰下的检测

假设LFM信号的起始频率为f0＝10MHz，调频率为β＝10×106MHz／s，采样率为80MHz，采样快拍数为200，噪声为零均值的高斯白噪声.从图2中可以看出，对于较大的信噪比如图2a所示，基于RWT的信号检测效果非常好.随着信噪比的减小，依然保留了较多的有关信号信息，保持了很好的检测能力，如图2b所示.当信噪比进一步下降，基于RWT的信号检测效果虽然有所下降，但如果提高检测门限，仍能将信号从噪声中正确检测出来，如图2c所示.

图2 基于RWT的信号检测Fig.2 Signal detection basing on RWT

图3给出了在虚警概率为Pf＝5×时，不同信噪比情况下基于RWT和基于FRFT最大值检测方法［10］的检测概率，由图3可见该方法比基于FRFT最大值检测方法在检测概率同为1时小6dB左右，说明该方法具有较好的抗噪声能力，这是因为该方法充分利用了信号的时频汇聚特性.

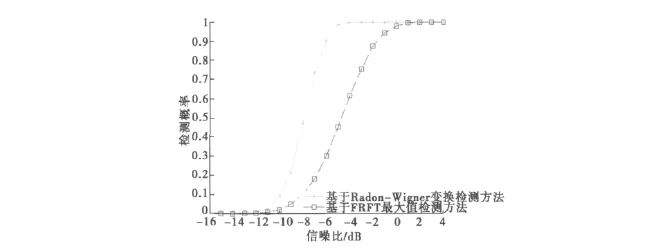
图3 不同信噪比下的检测概率Fig.3 Detection probability in different SNR

3.2 多信号的检测

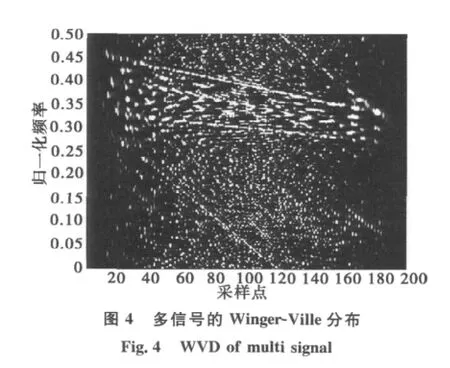
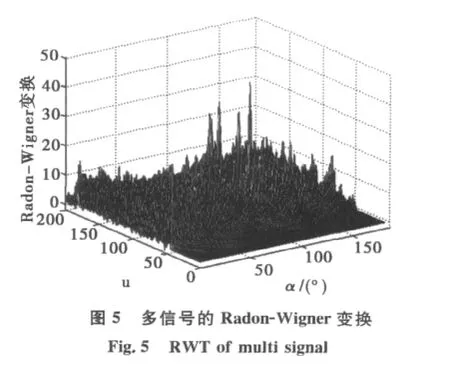
当接收信号为多个LFM信号时，假设接收信号中有4个LFM信号，起始频率分别为f10＝10MHz，f20＝5MHz，f30＝f40＝20MHz，调频率分别为：β1＝β2＝10×106MHz／s，β3＝5×106MHz／s，β4＝40×106MHz／s，并混有高斯白噪声，信噪比为－5dB.从图4中可以看到在利用WVD分析多个信号时存在着严重的交叉项，因此影响了对有用信号的检测.由于信号项在WVD平面表现为直线，变换到Radon平面则为一尖峰，而交叉项则会散布开，如图5所示.从图中可以看到有非常突出的4个尖峰，分别对应了4个信号项，而交叉项和噪声引起的干扰很小，因此4个LFM信号可以容易地检测出来.

4 结束语

研究了对LFM信号进行检测的方法，针对LFM信号的非平稳性特点，利用RWT的时频聚集特性，实现了LFM信号的检测，并对其检测性能进行了分析，得到了噪声背景下RWT输出信噪比，其中增大数据长度N是改善信噪比的一个有效手段.并推导了高斯白噪声下的检测概率，可以得到在给定虚警概率情况下的检测概率.仿真实验验证了这种方法的有效性.

［1] LIN Yan，PENG Yingning，WANG Xiutan.Maximum likelihood parameter estimation of multiple chirp signals by a new Markov chain Monte Carlo approach［Z］.IEEE proc Radar Conference，Philadelphia，2004.

［2] 董晖，姜秋喜.低信噪比下宽带LFM信号检测技术［J］.电子信息对抗技术，2008，23（1）：5－8，21.DONG Hui，JIANG Qiuxi.Broadband LFM signal detecting technologies under low SNR conditions［J］.Electronic information warfare technology，2008，23（1）：5－8，21.

［3] HAYKIN S，BHATTACHARYR T.Wigner－Ville distribution：an important functional block for radar target detection in clutter［Z］.Conference on Signals，Systems and Computers，Los Alamitos，1994.

［4] FRAZER G J，ANDERSON S J.Wigner－Ville analysis of HF radar measurements of an accelerating target［Z］.Proceeding of the Fifth International Symposium on Signal Processing and Its Applications，Brisbane，1999.

［5] ZOU Hongxing，LU Xuguang，DAI Qionghai，et al.Nonexistence of cross－term free time－frequency distribution with concentration of Wigner－Ville distribution［J］.Science in China，2002，45（3）：174－180.

［6] 邓兵，陶然，曲长文.分数阶Fourier域中多分量chirp信号的遮蔽分析［J］.电子学报，2007，36（6）：1094－1097.DENG Bing，TAO Ran，QU Changwen.Analysis of the shading between multicomponent chirp signals in the fractional Fourier domain［J］.Acta Electronica Sinica，2007，36（6）：1094－1097.

［7] 张贤达，保铮.非平稳信号分析与处理［M］.北京：国防工业出版社，1998：21－254.ZHANG Xianda，BAO Zheng.Nonstationary signal analysis and processing［M］.Beijing：Defense Industry Press，1998：21－254.

［8] BARBAROSSA S.Analysis of multi component LFM signals by a combined Wigner－Hough transform［J］.IEEE Transactions on Signal Processing，1995，43（6）：1511－1515.

［9] 陈小龙，关键，于仕财，等.海杂波背景下基于FRFT的多运动目标检测快速算法［J］.信号处理，2010，26（8）：1174－1180.CHEN Xiaolong，GUAN Jian，YU Shicai，et al.A fast detection algorithm of multiple moving targets in sea clutter based on FRFT［J］.Signal Processing，2010，26（8）：1174－1180.

［10] 尉宇.线性调频和非线性调频信号的检测与参数估计［D］.武汉：华中科技大学，2005.WEI Yu.The detection and parameter estimation of the linear frequency modulated signals and no linear frequency modulated signal in low SNR［D］.Wuhan：Huazhong University of Science ＆Technology，2005.