Ru掺杂SnO2半导体固溶体的电子结构研究

解学佳 钟丽萍 梁镇海＊, 樊彩梅 韩培德

(1太原理工大学化学化工学院，太原 030024)(2太原理工大学材料科学与工程学院，太原 030024)

Ru掺杂SnO2半导体固溶体的电子结构研究

解学佳1钟丽萍1梁镇海＊,1樊彩梅1韩培德2

(1太原理工大学化学化工学院，太原 030024)(2太原理工大学材料科学与工程学院，太原 030024)

运用基于密度泛函理论的第一性原理方法，建立了SnO2以及不同比例Ru掺杂的SnO2超胞模型，在对其进行几何优化后计算了 Sn1-xRuxO2(x=0，1/16，1/12，1/8，1/6，1/4，1/2)半导体的电子结构，并讨论了其晶格参数、电荷密度、能带结构和态密度(包括分态密度)等性质。结果表明，掺杂后，晶格参数随掺杂量的增加线性减小，与实验值的偏差在4%以内；掺杂后，在费米能级处可以提供更多的填充电子，使得电子跃迁至导带更容易，固溶体的导电性增强。为Sn1-xRuxO2固溶体电极材料的发展和应用提供了理论基础。

Ru掺杂SnO2；第一性原理；半导体固溶体；电子结构

0 引 言

1965年Beer[1]发明了RuO2-TiO2涂层钛阳极，即Dimensionally Stable Anode(简记为DSA)电极，且被成功运用于氯碱工业，此项突破很大程度上推动了电化学工业的发展。但是，在应用的过程中，依然存在许多弊端，如阳极生成的活性氧会将钛基体氧化而生成不导电的TiO2，致使其导电性降低[2-3]。据相关文献报道，此缺点可以通过在钛基表面涂抹一种或多种中间层使其形成固溶体结构来解决，其中以含有RuO2、SnO2、TiO2等一种或多种金属氧化物的电极催化效果较好[4]。例如，2002年，张乃东等[5]用电镀法制备了Ti/SnO2-Sb2O4氧化物电极，其可使Ti基体完全被覆盖，避免了由于TiO2裸露而产生的导电性和析氧电位的下降；李善评等[6]用浸渍法制备了La掺杂Ti/Sb-SnO2电极，发现该掺杂电极具有更高的析氧电位和更长的电极寿命；2013年，陈野等[7]采用溶胶凝胶法制备了Ni2+掺杂的Ti/SnO2-Sb2O5电极，结果表明，Ni2+的掺入细化了SnO2晶粒，增大了电极的比表面积，改善了电极表面的龟裂程度，提高了电极的导电性能；Zainullina[8]用第一性原理方法研究了SnO2晶体的能带结构；Liang等[9]计算了Sn0.5Sb0.5O2的电子结构和稳定性，分析了掺杂前后的电子密度、键长和态密度等性质，但是掺杂前后的电荷密度没有发生明显变化；徐剑等[10]对F掺杂SnO2体系的光学性质进行了一系列计算与分析，发现掺杂后其光学吸收边发生了蓝移，掺杂对光吸收具有调节作用；Yao等[11]对Mn掺杂SnO2体系进行了理论计算，并对其电子结构和光学特性进行了一系列分析，掺杂后吸收光谱发生红移，吸收边变窄；贾金乾等[12]计算了Ti掺杂SnO2的晶格常数和电子结构，说明当掺杂比例为0.5时，体系稳定性最强；于峰等[13-14]分别对N和Al掺杂SnO2的电子结构、态密度及光学性质进行了理论计算和分析，发现当掺杂比例增大时，折射率和消光系数的谱线均发生了蓝移；Zhou等[15]计算了W掺杂SnO2体系的能带结构和光学性质。由此我们可以看出，利用第一性原理的方法计算氧化物涂层的相关性质是一种非常重要的手段，已成为近年来的研究热点。但是对于Ru掺杂SnO2半导体的理论计算还未见报道，由于Ru掺杂SnO2半导体是一种非常经典的耐酸阳极材料，因此从理论的角度对其性能进行探讨，对钛阳极性能的优化具有理论指导作用。

本文运用基于密度泛函理论(Density Functional Theory，简记为 DFT)[16]的第一性原理方法对Sn1-xRuxO2半导体的电子结构进行了计算和分析，为DSA光电材料的工业化生产提供一定的理论依据。

1 晶胞模型与计算方法

1.1 晶胞模型

理想SnO2是金红石相，属体心四方晶系，对称性为,空间群为P42/mnm,晶格常数:a=b=0.473 7 nm，c=0.318 6 nm，α=β=γ=90°[17]。 如图 1 所示每个SnO2单胞中含有2个Sn原子，分别位于四方体的顶点和体心位置，其坐标为(0，0，0)和(1/2，1/2，1/2)，含有4个O原子，其中2个位于四方体的面上，另外2个位于内部，形成歪曲的六方最紧密堆积结构。SnO2晶体结构可看成是Sn-O八面体以共棱方式连接成链，而链与链之间以共顶方式相连形成[10]。由于SnO2和RuO2都属金红石结构，且晶格常数非常接近 (RuO2，a=b=0.449 9 nm，c=0.310 7 nm，α=β=γ=90°)，可形成固溶体，这也与有关实验结果[18]相符。

图1 SnO2单胞模型Fig.1 Models of unit cell of SnO2

计算时，我们首先建立晶胞模型，本文对SnO2采用原子替代法，用Ru原子直接置换超晶胞中的一个Sn原子，例如Sn0.5Ru0.5O2是将图1中Sn2原子替换为Ru原子，掺杂比例与超晶胞对应关系如表1所示。

表1 Sn1-xRuxO2半导体中对应掺杂比例Table 1 Correspondence proportions of Ru inSn1-xRuxO2semiconductor

1.2 计算方法

利用Accelrys公司开发的Materials Studio软件包中的CASTEP[19]模块进行计算，CASTEP是一个基于DFT的第一性从头算量化计算程序。本文采用的是基于DFT的平面波超软赝势(USPP)方法。计算分两步完成，首先对已建立的晶胞模型进行几何优化，以找到半导体结构的最稳定状态；然后对己优化的晶胞模型进行能带结构、电子态密度以及电荷密度等性质的计算。本文选择用广义梯度近似法(简记为GGA)进行计算，然后用PBE方案进行校正，采用超软赝势描述价电子和离子间的相互作用[20]。布里渊区积分采用 4×4×6的 Monkorst-Park方案[21-22]，平面波截断能选择在380 eV，所有计算都在倒易空间中进行。计算中所有可能构型的优化均采用BFGS算法，迭代过程中的收敛精度为 2.0×10-5eV·atom-1，最大位移为 2.0×10-4nm，原子间相互作用力收敛标准设定为 0.3 eV·nm-1，内应力不大于 0.1 GPa。选取的价电子组态分别为Ru：4s24p64d75s1，O：2s22p4，Sn：5s25p2。

2 结果与讨论

采用以上参数，首先对SnO2的晶胞结构进行优化，分别计算截断能 Ecut-off为 260、300、340、380 和400 eV时体系的晶格参数和总能量，结果列于表2中，由计算结果可以看出，截断能在260～340 eV区间内时，参数均逐渐减小，且变化较大，从380 eV开始随着截断能的增加，体系总能量开始收敛，变化了0.000 98%，基本达到稳定状态，此结果与Liu等[23]的计算结果一致。而且，Liang[9]和Zhou[15]等在计算SnO2相关掺杂情况时均采用了380 eV的截断能计算。所以综合考虑计算时间和内存的因素，在电子结构和态密度的计算中平面波截断能最终设置为380 eV，此时的晶格常数分别为a=b=0.490 2 nm和c=0.328 3 nm，与实验值[24]和其他第一性原理计算结果[23,25]的误差均在4%以内。在此后的计算中，我们均采用优化好的晶格参数。

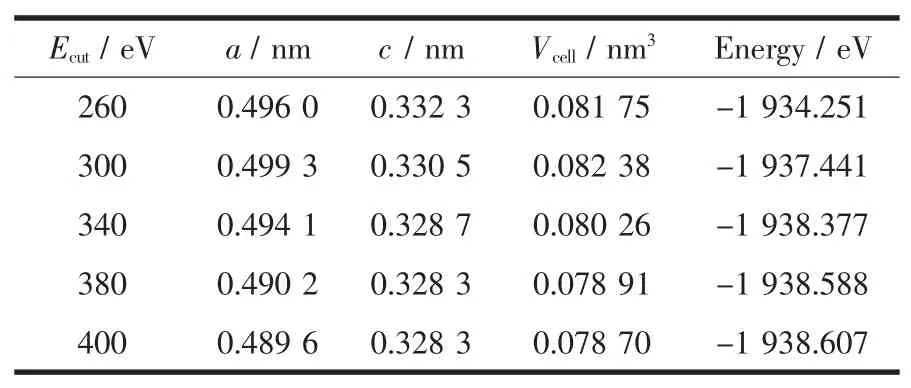
表2 不同截断能下SnO2的晶胞参数Table 2 Optimal parameter of SnO2with different cut-off energy

2.1 体系优化

对不同比例的Ru掺杂SnO2模型用CASTEP进行结构优化，优化后模型的各边长均发生了变化，图2所示为晶格参数a和体积V随掺杂量的变化情况。由图2可以看出，随着Ru掺杂量的增大,晶格参数a线性减小，晶胞体积也呈现同样的变化趋势，符合Vegard′s定律，说明该实验结果是合理的。这里减小的趋势是由于Ru4+的半径(0.065 nm)小于Sn4+的半径(0.071 nm)，所以Ru的掺杂比例越大，晶胞体积就越小，此结果与Gaudet等[26]的实验规律一致;当x=0.5时，晶格参数的计算值 (a=0.473 7 nm，c=0.320 8 nm)与 实 验 值[26](a=0.473 8 nm，c=0.318 7 nm)较接近，误差在小于 0.65%。造成理论值与实验值存在误差的原因在于理论计算中非化学因素的影响及温度的忽略[12]，但是误差较小，说明本文所采用的计算方法可行，结果合理。

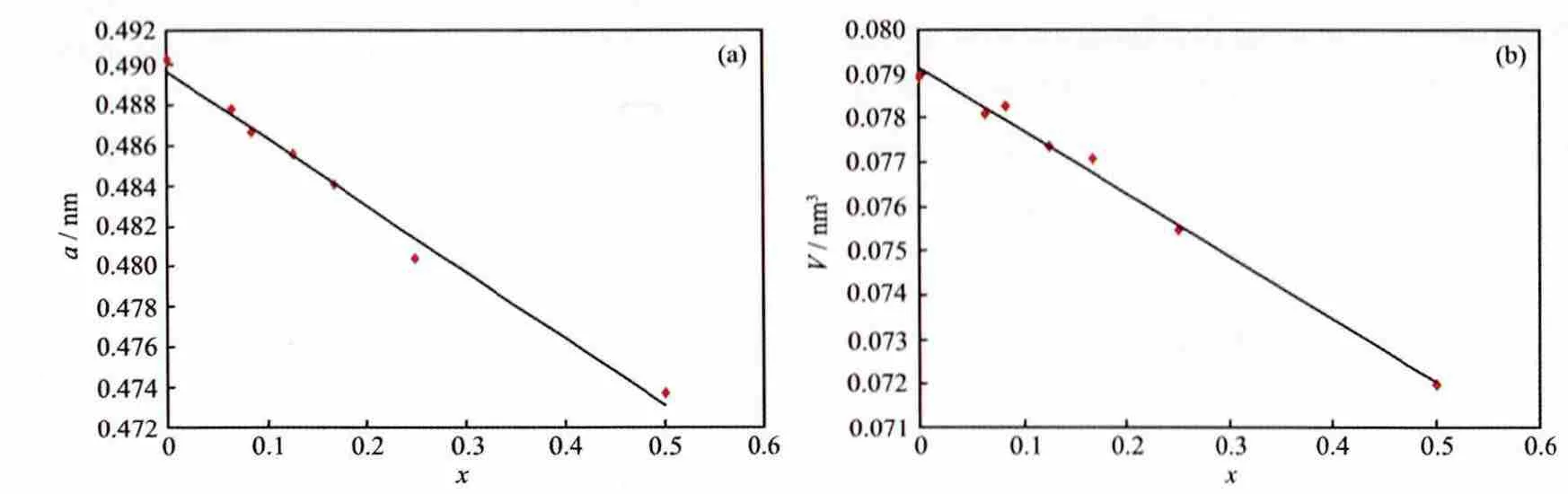
图2 计算得Sn1-xRuxO2半导体的晶格参数a和晶胞体积V与掺杂比例x的关系Fig.2 Calculated lattice parameters of a and unit-cell volume as a function of x for Sn1-xRuxO2semiconductor

2.2 Mulliken布居分析、电荷密度及差分密度

即使原子电荷布居分析对所采用的基函数具有相当高的灵敏度，所得原子有效电荷的大小并没有绝对的物理意义，但如果计算时所采用的基函数相同，原子电荷和布居分析的相对大小就可以提供有价值的信息，用来比较其性质[27-28]。所以表3计算了掺杂前后晶胞中原子的电荷布居。

由表3可以看出，掺杂后，O1、O2原子的有效电荷数由掺杂前的-0.92e变为-0.63e，O3、O4原子的有效电荷由-0.92e变为-0.79e，其变化都是主要发生在p轨道上，s轨道上的Mulliken布居数变化不大；Sn1原子的有效电荷数由掺杂前的1.83e增大到1.94e，说明掺杂后失去电子数比掺杂前略有所增多，Sn1与O之间的离子性增强；替代Sn2原子位置的Ru原子的有效电荷为0.89e，比掺杂前此位置的Sn2原子的有效电荷数小的多，说明它比Sn2原子失去的电子数少。

表3 SnO2and Sn0.5Ru0.5O2的原子Mulliken布居分析Table 3 Atomic Mulliken-population analysis of SnO2and Sn0.5Ru0.5O2

表4表示掺杂前后原子间的重叠布居数及键长，通过分析可知，掺杂后Ru1与每个O原子的重叠布居数分别大于掺杂前Sn2与每个O原子的重叠布居数，其键长也相应减小，说明掺杂体系中Ru-O键结合强度大于Sn-O键的结合强度，即Ru-O键的共价性大于Sn-O键。而掺杂后Sn1-O1/O2和Sn1-O3/O4的布居数均减小，这表明掺杂Ru后使Sn1-O之间的重叠程度减小，但是其键长反而比掺杂前短，这种现象与He等[29]的研究结果一致。导致这种情况的原因可能有两点：(1)掺杂后，Sn1-O的布居数减小，说明Sn1与O原子之间的电子重叠程度减小，但键长反而变短，这是由于Sn1与O原子之间的共价性减小和离子性增强所致，且共价性减小的程度要小于离子性增强的程度，因而导致了此现象，这一点也可以从表3的计算结果中看出；(2)掺杂后，由于体心Ru原子半径小于掺杂前Sn原子，所以对周围O原子及Sn原子的作用力大于掺杂前体心Sn原子对周围原子的作用力，这也与掺杂后晶胞参数变小的现象符合。综合以上两种因素考虑，导致了重叠数变小，键长变小的情况发生。

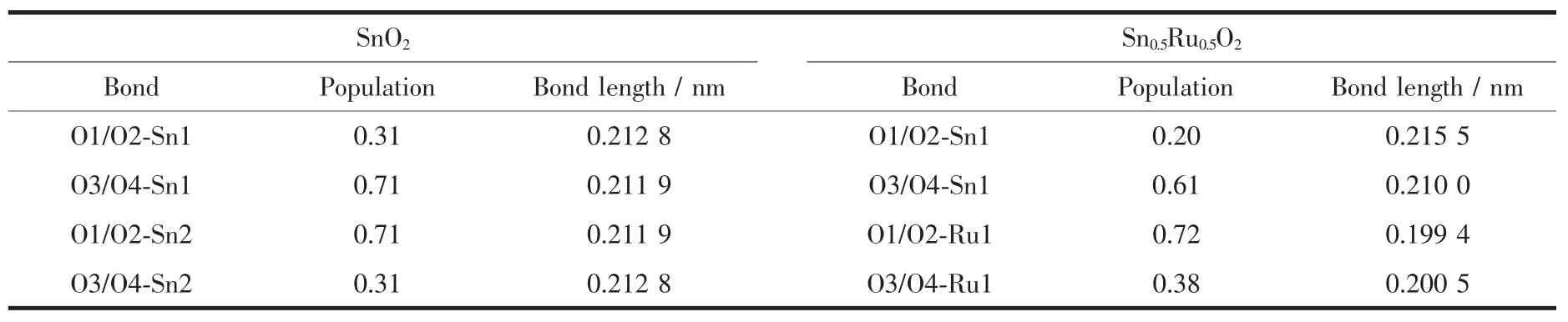
表4 SnO2and Sn0.5Ru0.5O2的键长和重叠布居数Table 4 Bond lengths and overlap populations of SnO2and Sn0.5Ru0.5O2

图3的 (a)和 (b)分别列出了本征SnO2和Sn0.5Ru0.5O2半导体中(110)面的电荷密度分布，通过对比掺杂前后的电荷密度分布图可知，Ru原子周围的电荷密度明显要大于Sn原子周围的电荷密度。掺杂前，Sn原子与O原子周围的电子云重叠程度较小，说明Sn、O原子间主要形成离子键；掺杂后，该位置Ru原子与O原子之间有较大程度的电子云重叠，说明Ru、O原子之间的相互作用要强于Sn、O原子，共价性也相应的变大，表4中键的布居分析也说明了该点。

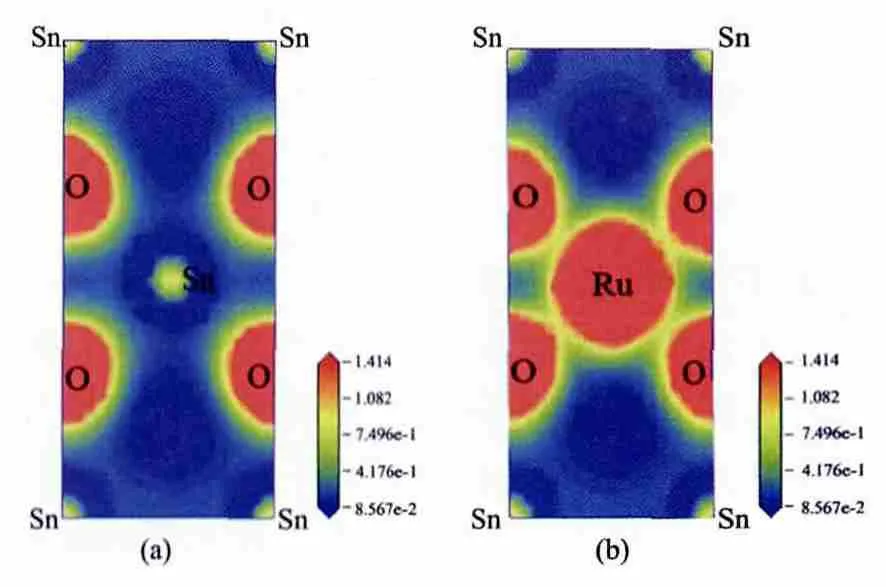
图3 Sn1-xRuxO2的电荷密度分布图 [(a)x=0;(b)x=0.5]Fig.3 Plots of charge density contour of Sn1-xRuxO2[(a)x=0;(b)x=0.5]

图 4(a)和(b)分 别 表 示 本 征 SnO2和 Sn0.5Ru0.5O2半导体中面的电荷差分密度，图中蓝色区域和红色区域分别表示电荷密度减小(Δρ＜0)和增加(Δρ＞0)。 差分密度 Δρ通过公式 Δρ=ρdefect-∑(ρi)[30]求得，其中：ρdefect为掺杂体系优化后的总电荷密度分布函数，ρi为体系中优化前的某原子的电荷密度分布函数。对比两图可以看出，被替换的原子周围的电荷分布发生了明显的变化，掺杂前，O原子周围的电荷密度增加，Sn原子的电荷密度减小，O原子得到电子而Sn原子失去电子，Sn、O原子间的离子性较强，这与杜晔平等[31]的研究结果一致；掺杂后，Ru原子周围的电子显示出明显的方向性变化，这可能是因为在掺杂后的体系中Ru和O以d2sp3的杂化方式形成半导体，O原子上的孤电子对进入Ru原子的杂化轨道，形成配位键；而Ru原子的4d轨道又与配体O原子的2p轨道重叠，Ru原子上的电子又流回O的2p轨道，形成反馈π键，反馈π键的形成对O与Ru键合度的增强起到了关键作用。

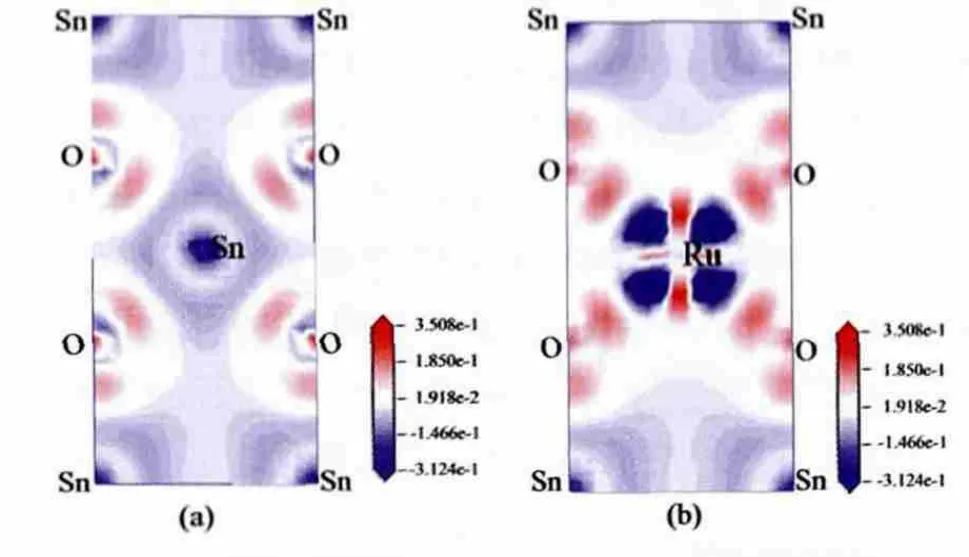
图4 Sn1-xRuxO2的电荷差分密度图[(a)x=0;(b)x=0.5]Fig.4 Plots of differences of charge density contour ofSn1-xRuxO2[(a)x=0;(b)x=0.5]

2.3 能带结构与态密度

为了便于讨论掺杂对SnO2电子结构的影响，首先对未掺杂的SnO2的能带结构和电子态密度进行了计算，结果如图5、图6所示。

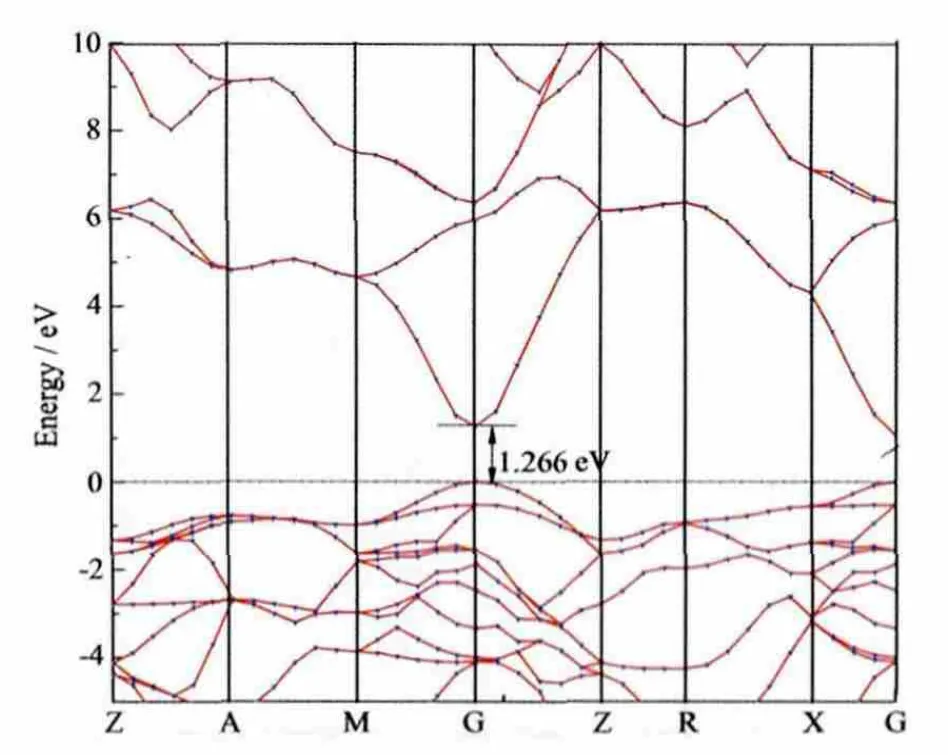
图5 SnO2的能带结构图Fig.5 Bond structures of SnO2

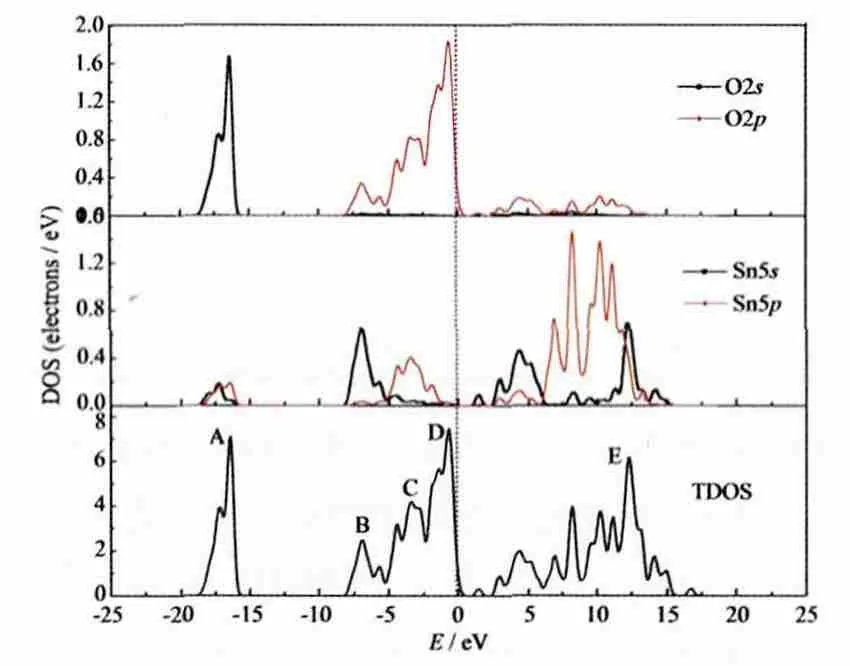
图6 SnO2的态密度图Fig.6 Density of states for SnO2

图5为SnO2的能带结构图，将Fermi能级EF选在0 eV处。从图中可以看出，SnO2的导带最低点(conduction band minimum，简记为CBM)与价带最高点 (valence band maximum，简记为VBM)均在Brillouin区的G点处，因此属直接带隙，计算所得SnO2带隙值为1.266 eV，说明SnO2是一种直接带隙半导体。此结果与Liang等[9]、贾金乾等[12]、刘亚明等[23]的计算结果 1.1 eV、1.5 eV、1.258 eV 基本一致。虽然采用GGA获得了很好的晶格参数，但计算的带隙远小于实验值3.6 eV[32]，这是DFT计算带隙普遍存在的通病，原因是：由于DFT属于基态理论，局域密度泛函理论中KS方程的本征值不能准确地给出系统的激发态能量，使得位于导带的电子态能量值比实验值低[12]，即计算所得的带隙值是基态情况下的带隙，而实验所得带隙值属激发态下的带隙，所以造成了理论与实验的偏差。由于本文比较的是掺杂前后相对值的变化，所以计算带来的误差并不影响定性分析[33]，而且计算理论本身存在不足，在DFT的电子交换关联函数中，GGA对能隙的结果计算普遍偏低[34]。

图6为SnO2的态密度图，先前的工作已对其进行了详细研究[12,23]。从图中的总态密度(TDOS)和分态密度(PDOS)我们可以看出，位于Fermi能级左边约-15到-20 eV处的价带底的A峰主要是来自O2s态的成分，另有少量的Sn5s和Sn5p态的贡献，但是该峰距Fermi能级较远，对应深轨能级，对Fermi能级附近电子的影响很小。价带顶部区域的宽度约为8.3 eV，由B、C和D三部分构成，其中下价带B峰，主要是来自O2p和Sn5s态的贡献，宽度约为3.3 eV；C峰主要是O2p和Sn5p轨道的贡献，宽度约为2.5 eV；而上价带D峰主要是O2p态的作用。范围在1.6～5.4 eV的导带底区域主要是由Sn5s和O2p轨道杂化构成，导带的高能部分则由Sn5p以及少量的Sn5s和O2p共同构成。从图中可以看出，Sn和O的电子态贡献都很明显，表现为SnO2是具有一定共价性的离子键晶体[23]。

图 7 给 出 了 掺 杂 体 系 Sn0.5Ru0.5O2的 能 带 结 构图，由图可以看出：掺杂后，导带底部几乎与费米能级相交，说明掺杂后的固溶体显示金属性，这是与本征SnO2完全不同之处，原因在于RuO2本身，其带隙为零[35]，显示金属性，导致掺杂后形成的固溶体也显示金属性。与纯净的SnO2相比，掺杂Ru后，晶体的价带和导带的数目明显变密、增多，这说明Ru原子掺入SnO2后，确实使晶体的导电性从非金属性向金属性发展。

图7 Sn0.5Ru0.5O2的能带结构图Fig.7 Bond structures of Sn0.5Ru0.5O2

图 8 是 Sn0.5Ru0.5O2掺 杂 体 系 的 态 密 度 图 ，与SnO2的态密度图对比可知：掺杂体系中，在距Fermi能级较远的地方产生了2个新峰，其分别由Ru5s和Ru4p态贡献产生，由于其属于深轨能级，因此在半导体中并不起成键作用；在距离Fermi能级6 eV左右的VBM处，Ru4d起到了少许作用；导带部分主要由Ru4d、Sn5s、Sn5p态相互作用形成，其中，CBM处主要是Ru4d的贡献，由峰形可以看出，其局域性较强。相对未掺杂的SnO2，杂质Ru的引入致使Ru4d态对CBM和VBM的态密度发生变化，波体整体向低能方向偏移了2 eV，在禁带中形成了由Ru4d和O2p轨道杂化的中间能带，大幅减小了价电子所需的激发能量。

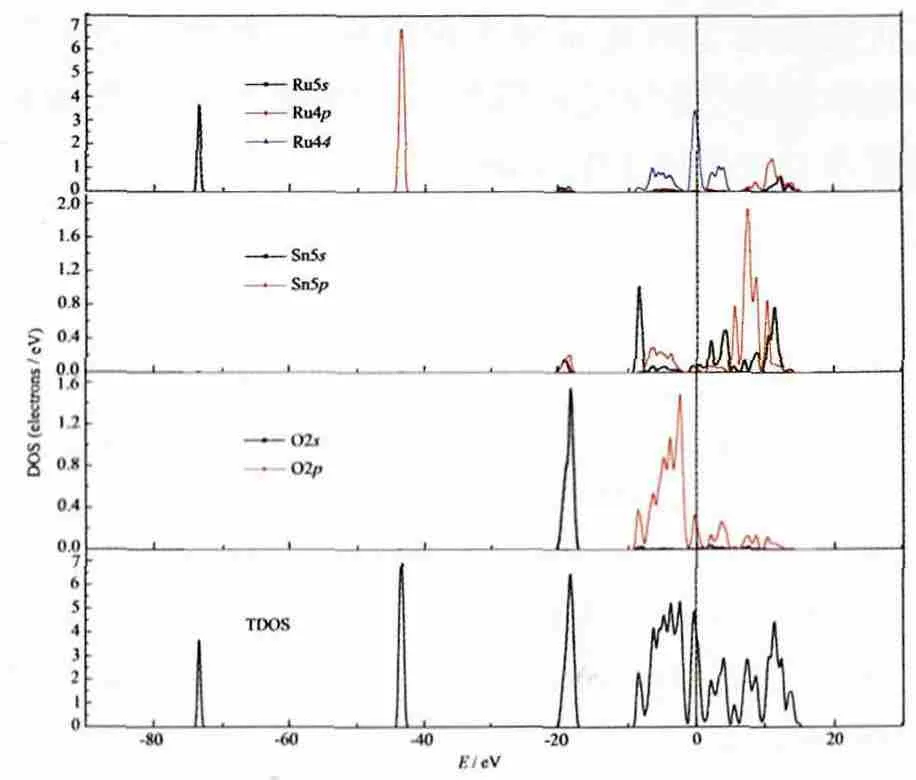
图8 Sn0.5Ru0.5O2的态密度图Fig.8 Density of states for Sn0.5Ru0.5O2

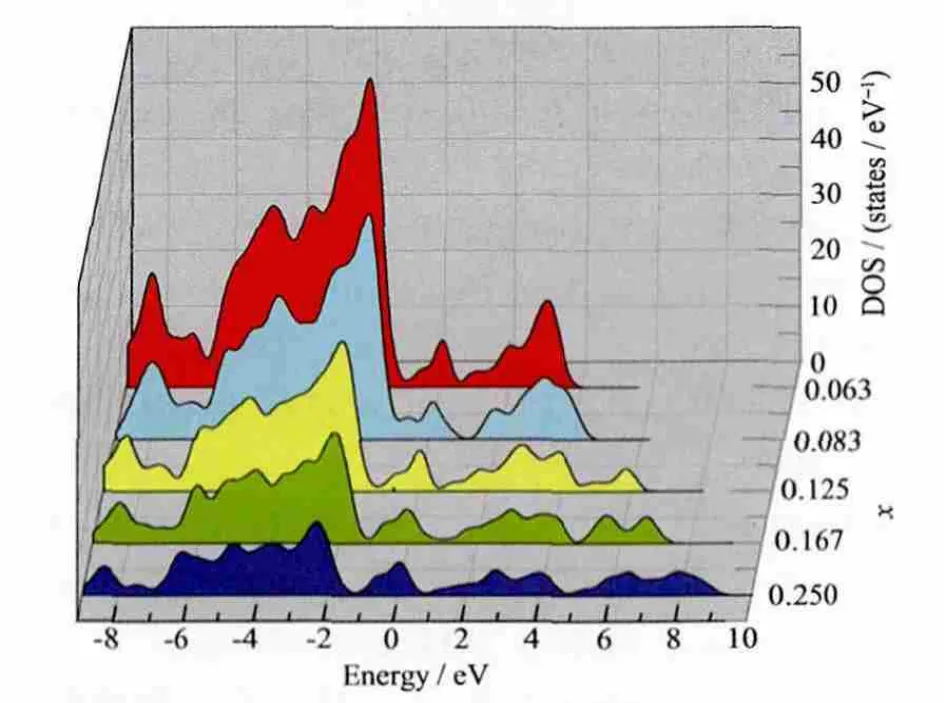
图9 不同Ru掺杂比例的Sn1-xRuxO2固溶体的总态密度图Fig.9 Total density of state of Sn1-xRuxO2solid solutions with different Ru doping amounts

图9为不同掺杂比例下Sn1-xRuxO2的总态密度图，从图中可以看出，随着掺杂比例的增加，导带部分逐渐展宽，表明电子在该区域的离域性有所增强，同时费米能级附近的导带底也有小幅度的增宽并向低能方向扩展，这将使得价带中的一部分电子跃迁至导带中更容易，并且高浓度的掺杂使得带隙中产生了更宽的杂质能级，这也表明费米能级附近处可填充的电子数有所增加。为定量分析不同浓度Ru掺杂比例在导带底产生可填充的电子数，分别对不同掺杂浓度下Sn1-xRuxO2超晶胞的态密度从0 eV到2.5 eV进行了积分，结果表明：Ru掺杂比例为 0.063、0.083、0.125、0.167 和 0.250 时， 费米能级处可填充的电子数分别为12、8、7、6和5，这说明掺杂Ru后在费米能级处可以提供更多的填充电子，这将使得电子跃迁至导带更容易，因此使得电极的导电性增强，这与实验结果也比较符合[36]，且当掺杂浓度为0.063时导电性最大。

[1]Beer H B.J.Electrochem.Soc.,1980,127(8):303C-307C

[2]LIANG Zhen-Hai(梁镇海),SUN Yan-Ping(孙彦平).J.Inorg.Mater.(Wuji Cailiao Xuebao),2001,16(1):183-187

[3]HUANG Yun-Tao(黄运涛),PENG Qiao(彭乔).Rare Metal Mater.Eng.(Xiyoujinshu Cailiao Yu Gongcheng),2006,35(10):1610-1615

[4]Palmas S,Polcaro A M,Ferrara F,et al.J.Appl.Electrochem.,2008,38(7):907-913

[5]ZHANG Nai-Dong(张乃东),LI Ning(李宁),PENG Yong-Zhen(彭永臻).Chinese J.Inorg.Chem.(Wuji Huaxue Xuebao),2002,18(11):1173-1176

[6]LI Shan-Ping(李善评),CAO Han-Lin(曹翰林),HU Zhen(胡振).Chinese J.Inorg.Chem.(Wuji Huaxue Xuebao),2008,124(3):369-374

[7]CHEN Ye(陈野),XU Wei-Chao(许维超),DUAN Ti-Gang(段体岗).Chinese J.Inorg.Chem.(Wuji Huaxue Xuebao),2013,29(2):243-248

[8]Zainullina V.Phys.B,2007,391(1):280-285

[9]Liang Z H,Ding Y B,Jia J Q,et al.Phys.B,2011,406(11):2266-2269

[10]XU Jian(徐剑),HUANG Shui-Ping(黄水平),WANG Zhan-Shan(王占山),et al.Acta Phys.Sin(Wuli Xuebao),2007,56(12):7195-7200

[11]Lu Y,Wang P J,Zhang C W,et al.Phys.B,2011,406(17):3137-3141

[12]JIA Jin-Qian(贾金乾),XIE Xue-Jia(解学佳),LIANG Zhen-Hai(梁镇海),et al.Chem.J.Chinese Universities(Gaodeng Xuexiao Huaxue Xuebao),2012,33(5):1050-1056

[13]Yu F,Wang P J,Zhang C W.Acta Phys.Sin.,2010,59(10):7285-7290

[14]YU Feng(于峰),WANG Pei-Ji(王培吉),ZHANG Chang-Wen(张昌文).Acta Phys.Sin.(Wuli Xuebao),2011,60(2):023101

[15]Zhou W,Liu L J,Yuan M Y,et al.Comput.Mater.Sci.,2012,54:109-114

[16]Hohenberg P,Kohn W.Phys.Rev.,1964,136(3B):B864-B871

[17]Haines J,Léger J M.Phys.Rev.B,1997,55(17):11144-11154

[18]Gaudet J,Tavares A C,Trasatti S,et al.Chem.Mater.,2005,17(6):1570-1579

[19]Segall M D,Lindan P L D,Probert M J,et al.J.Phys.:Condens.Matter,2002,14(11):2717-2744

[20]Perdew J P,Burke K,Ernzerhof M.Phys.Rev.Lett.,1996,77(18):3865-3868

[21]Pack J D,Monkhorst H J,Freeman D L.Solid State Commum.,1979,29(10):723-725

[22]Monkhorst H J,Pack J D.Phys.Rev.B,1976,13(12):5188-5192

[23]LIU Ya-Ming(刘亚明),YAO Shu-Wen(姚树文),LIU Yu-Bo(刘玉波).J.Henan I.Sci.Technol.(Henan Keji Xueyuan Xuebao),2011,39(1):78-82

[24]Klementová M,Rieder M,Weiss Z.J.GEO Sci.,2000,45(1-2):155-157

[25]Oviedo J,Gillan M.J.Surf.Sci.,2001,490(3):221-236

[26]Rantala T T,Rantala T S,Lantto V.Mater.Sci.Semicond.Process,2000,3(1-2):103-107

[27]FANG Li-Min(房丽敏).Acta Phys.Sin.(Wuli Xuebao),2011,60(5):056801

[28]Winkler B,Pickard C J.Phys.Rev.B,2001,63:214103

[29]HE Jian-Ping(何建平),LÜ Wen-Zhong(吕文中),WANG Xiao-Hong(汪小红).Acta Phys.Sin.(Wuli Xuebao),2011,60(9):097102

[30]CHEN Jian-Hua(陈建华),ZENG Xiao-Qin(曾小钦),CHEN Ye(陈晔),et al.Chin.J.Nonferr.Met.(Zhongguo Youse Jinshu Xuebao),2010,20(4):765-771

[31]DU Ye-Ping(杜晔平),CHEN Jing-Chao(陈敬超),FENG Jing(冯晶).Acta Phys.-Chim.Sin.(Wuli Huaxue Xuebao),2009,25(2):278-284

[32]Dolbec R,Saint R G,Trudeau M,et al.Thin Solid Films,2002,419(1-2):230-236

[33]ZHAO Zong-Yan(赵宗彦),LIU Qing-Ju(柳清菊),ZHANG Jin(张瑾),et al.Acta Phys.Sin.(Wuli Xuebao),2007,56(11):6592-6599

[34]LIN Wei(林伟),ZHANG Yong-Fan(章永凡),LI Yi(李奕),et al.Acta Phys.-Chim.Sin.(Wuli Huaxue Xuebao),2006,22(1):76-81

[35]Zhu Z G,Deka R C,Chutia A,et al.J.Phys.Chem.Solids,2009,70(9):1248-1255

[36]LIU Yu-Shuo(刘禹硕),LIU Yuan(刘元),LIU Hui-Ling(刘惠玲).Mater.Sci.Technol.(Cailiao Kexue Yu Gongyi),2010,18(6):810-814

Electronic Structures of Ru-Doped SnO2Semiconductor Solid Solutions

XIE Xue-Jia1ZHONG Li-Ping1LIANG Zhen-Hai＊,1FAN Cai-Mei1HAN Pei-De2
(1College of Chemistry and Chemical Engineering,Taiyuan University of Technology,Taiyuan 030024,China)(2College of Material Science and Engineering,Taiyuan University of Technology,Taiyuan 030024,China)

Ru-doped SnO2semiconductor is a significant component of titanium based oxide acid-resistant anode.Using the first-principle method based on the density functional theory,crystal cells were built,which include SnO2and variety proportions of Ru-doped SnO2,and electronic structures of Sn1-xRuxO2semiconductor(x=0,1/16,1/12,1/8,1/6,1/4,1/2)were calculated after geometry optimization.Lattice parameters,electron density,band structure,and density of states are discussed.The results show that the corresponding lattice parameters reduce linearly with composition and the errors between calculated and experimental values of that are within 4%;in addition,the number of electrons filled at the bottom of the conduction band increases after doping,resulting in the strengthening of the conductivity of the solid solution after doping of Ru.The results provide a theoretical basis for the development and application of the Sn1-xRuxO2solid solutions electrode.

Ru-doped SnO2;first-principles;semiconductor solid solutions;electronic structure

O649.4

：A

：100-4861(2013)12-2514-07

10.3969/j.issn.1001-4861.2013.00.344

2013-01-16。收修改稿日期：2013-05-21。

国家自然科学基金(No.20771080,21176168)；国家自然科学基金委员会和神华集团有限责任公司联合资助项目(No.U1261103)；山西省国际科技合作项目(No.2012081016)资助项目。

＊通讯联系人。 E-mail：liangzhenh@sina.com，liangzhenhai@tyut.edu.cn