突触信号传导的动态饱和模型研究

王金光

（山东外贸职业学院，山东 青岛 266100）

突触信号传导的动态饱和模型研究

王金光

（山东外贸职业学院，山东 青岛 266100）

对一类动态饱和突触神经模型中信号传导性质进行了研究。模型的动态过程采用高阶Milstein随机微分方程解法进行求解，其信号输入输出特性用集平均互相关系数进行衡量。集平均互相关系数的数值分析结果表明，适宜的噪声能够增强信号传导，并且通过调节饱和势比值大小和突触神经群体数目，观测到噪声增强信号传导的非线性现象更加显著。

突触神经模型；互相关系数；信号传导；噪声增强

0 引言

近30年的研究表明，噪声能够在非线性系统的信号传输中起到协同作用，这类非线性现象称为随机共振现象或噪声增强现象［1-7］。神经细胞中信号传导的非线性动态过程发生在噪声环境中，Longtin等［2］首次在FitzHugh神经元模型中实现了噪声增强现象。随后在Hodgkin-Huxley［3］、Hindmarsh-Rose［1］等神经元模型中均发现了噪声增强的信息处理现象。由于神经信号的非周期性质，Collins等［4］提出了非周期随机共振理论，这一理论的提出对于理解神经细胞、中枢神经乃至人脑的信息处理提供了一种新的思路。同时，非周期随机共振理论在人体平衡性［5］和人工耳蜗［6］等医学工程方面的实际应用发展迅速。中国国内学者对于各种神经元中的随机共振现象及其应用也进行了大量研究［8-13］，在语音处理［8］、神经网络功能［11-12］和图像复原［13］等方面取得了很多重要研究成果。

文献［1］～［6］，［8］～［13］主要分析了噪声协助弱信号克服细胞势电位发放的阈值，以达到提高信息传导效率的目的。但是，在突触神经信号传导水平中，还有一类饱和动态过程［7］，传导信号引发了突触间隙囊泡神经递质的释放。但是，由于突触囊泡群体的有限性，递质的释放活动具有一个饱和值，其信息传递过程可以用一类饱和突触模型［7］来描述。相对于传导信号来讲，突触神经细胞内外离子的随机活动可以视为白噪声。这些随机噪声对于饱和突触模型信号传导的影响值得深入研究。

本文主要针对一类饱和突触模型的信号传导特性进行了深入研究，首先利用改进的高阶Milstein解法［14］对模型所满足的随机微分方程进行了求解。用集平均互相关系数这个衡量指标对模型的信号输入输出特性进行了深入分析。集平均互相关系数的数值分析结果表明，适宜的噪声能够增强信号传导。通过调节饱和势比值的大小和势和兴奋性（抑制性）突触神经群体数目，发现噪声增强信号传导的现象更加显著。这些研究结果对于理解突触信号处理机制具有重要意义。

1 饱和突触模型及其解法

突触间隙囊泡神经递质活动的饱和动态模型为［7］

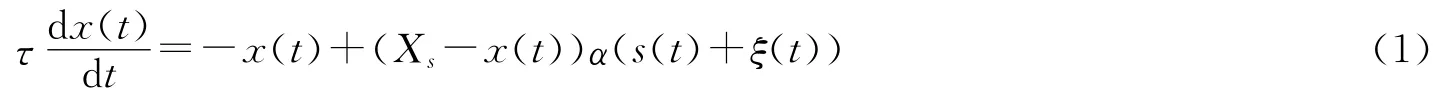
这里，τ＞0为松弛时间常数，α＞0为输入转化为输出的参数，Xs＞0为饱和势，s（t）为输入信号。非负噪声ξ（t）为伽马噪声，其分布为

由于式（1）中系数含有随机项，这里采用基于伊藤-泰勒展开的高阶Milstein随机微分方程解法［14］。将式（1）写为

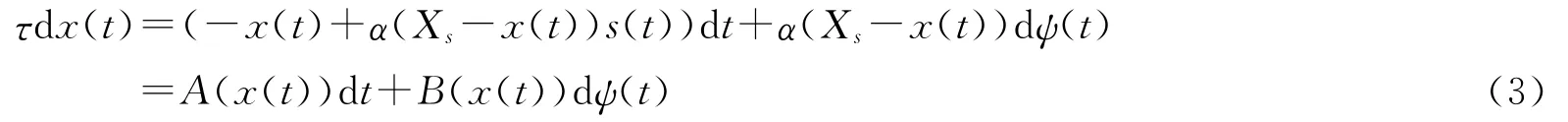
这里，A（x（t））=-x（t）+α（Xs-x（t））s（t），B（x（t））=α（Xs-x（t）），dψ（t）=ξ（t）dt。数值求解时，将时间进行离散化，采样时间Δt=ti+1-ti，i=0，1，2，…，那么Δψi=ψ（ti+1）-ψ（ti）。由初始值x（t0），过程x（t）在时刻ti+1的解为

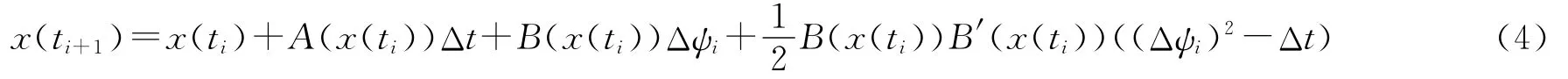
这里，B′（x（t））=-α。式（4）是由依据伊藤-泰勒展开的 Milstein迭代随机微分方程解，其收敛阶数比Euler-Maruyama解法高［14］。

为衡量非周期信号s（t）在此模型的传输特性，计算输入信号s（t）和系统输出x（t）的互相关系数

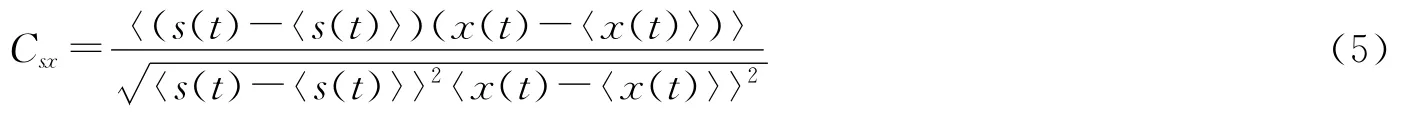
这里，〈·〉表示时间平均算子。实验中，互相关系数对于相同强度的不同噪声样本进行集平均，得到集平均互相关系数E［Csx］。

2 实验结果

进一步，考虑抑制性突触饱和神经元对于信号传输的影响。现实中存在兴奋性和抑制性两种突触神经元，当式（1）中饱和势Xs＞0时，突触神经是兴奋性的，当饱和势Xs变为XI（XI＜0），突触神经是抑制性的，即

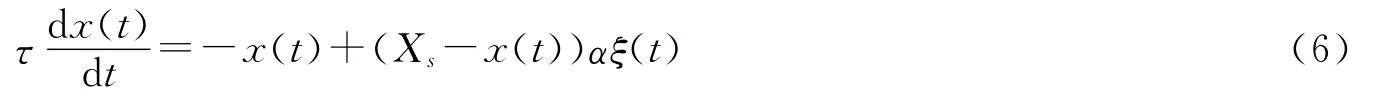
这里，抑制性突触饱和神经元释放抑制性递质，由于其离子通道动力学性质［15］，可以使他们的突触后神经元被抑制，这里仅考虑由噪声驱动。兴奋性突触神经元和抑制性突触神经元各选取1 000个，饱和势比值XI/Xs为-5/7、-1和-2，参数α=100。图2给出了集平均互相关系数E［Cxs］随着噪声强度（均方根r）的变化曲线。可以看出，抑制性突触神经元虽然只有噪声的驱动，但是在大量的抑制性突触神经元与兴奋性突触神经元组成的多信号传输通道中，集平均互相关系数E［Csx］依然对应了一个最优的噪声强度。并且，饱和势比值XI/Xs对于集平均互相关系数的影响较为明显，特别是XI/Xs=-1时，集平均互相关系数E［Csx］的最大值达到0.92，这是一种非常适合信号传输的突触神经元群体，这一结果对于理解突触信号处理机制具有重要意义。比如，如何优化饱和势比值XI/Xs来增强突触信号传导是值得进一步研究的问题，而且，现实中兴奋性突触神经元和抑制性突触神经元是否选择类似的优化策略来处理突触信号，更是值得探讨的研究方向。

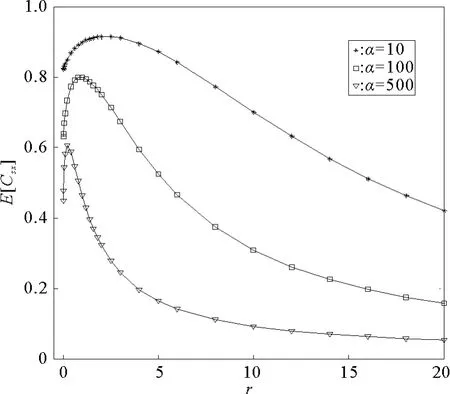
图1 集平均互相关系数E［Csx］随着噪声强度（均方根r）的变化Fig.1 Ensemble-averaged correlation coefficient as a function of the noise rms amplitude

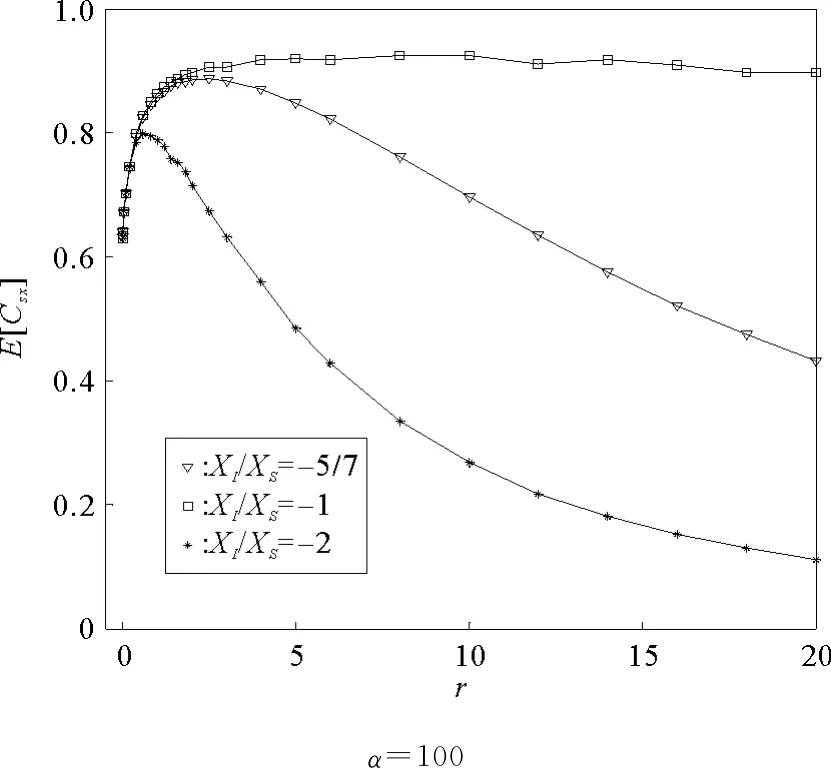
图2 集平均互相关系数E［Csx］随着噪声强度（均方根r）的变化Fig.2 Ensemble-averaged correlation coefficient as a function of the noise rms amplitude

3 结论

本文针对一类饱和突触模型的信号传导特性进行了研究，利用Milstein解法对模型所满足的随机微分方程进行了求解。用集平均互相关系数这个衡量指标对模型的信号输入输出特性进行了分析。集平均互相关系数的数值分析结果表明，适宜的噪声能够增强信号传导。同时，研究了大量的抑制性突触神经元与兴奋性突触神经元组成的多信号传输通道中噪声增强信号传导的现象，分析结果表明噪声强度能够优化集平均互相关系数，增强信号传导。不同的饱和势比值对于集平均互相关系数的影响非常显著，因此饱和势比值的优化非常值得进一步深入研究。

［1］Gammaitoni L，Hanggi P，Jung P，et al.Stochastic resonance［J］.Reviews of Modern Physics，1998，70（1）：233-287.

［2］Longtin A.Stochastic resonance in neuron models［J］.Journal of Statistical Physics，1993，70（1-2）：309-327.

［3］Gong Y，Xie Y，Hao Y.Coherence resonance induced by non-Gaussian noise in a deterministic Hodgkin Huxley neuron［J］.Physica A，2009，388（18）：3759-3764.

［4］Collins J J，Chow C C，Capela A C，et al.Aperiodic stochastic resonance［J］.Physical Review E，1996，54（5）：5575-5584.

［5］Dhruv N T，Niemi J B，Harry J D，et al.Enhancing tactile sensation in older adults with electrical noise stimulation［J］.Neuroreport，2002，13（5）：597-600.

［6］Morse R P，Evans E F.Enhancement of vowel coding for cochlear implants by addition of noise［J］.Nature Medicine，1996，2（8）：928-932.

［7］Chapeau-Blondeau F，Duan F，Abbott D.Synaptic signal transduction aided by noise in a dynamical saturating model［J］.Physical Review E，2010，81（2）：021124.

［8］薛凌云，向学勤，范影乐，等.基于神经元阈上非周期随机共振机制的语音复原技术研究［J］.传感技术学报，2009，22（2）：213-218.

Xue Linyun，Xiang Xueqin，Fan Yingle，et al.Speech restoration based on suprathreshold stochastic resonance of neuron model［J］.Chinese Journal of Sensors and Actuators，2009，22（2）：213-218.

［9］李冰，彭建华，刘延柱.随机延时 Hodgkin-Huxley神经网络的同步与联想记忆［J］.上海交通大学学报，2005，39（11）：1924-1928.

Li Bing，Peng Jianhua，Liu Yanzhu.The synchronization and associative memory of Hodgkin-Huxley neural network with randomly distributed time delays［J］.Journal of Shanghai Jiaotong University，2005，39（11）：1924-1928.

［10］王俊琦，焦贤发.基于IF模型阈值神经元的随机共振［J］.合肥工业大学学报，2010，33（6）：939-943.

Wang Junqi，Jiao Xianfa.Stochastic resonance of an integrate-and-fire neuron model with threshold［J］.Journal of Hefei University of Technology，2010，33（6）：939-943.

［11］曹明明，王景，段法兵.兴奋性神经群体的非周期信息传输研究［J］，复杂系统与复杂性科学，2009，6（4）：66-70.

Cao Mingming，Wang Jing，Duan Fabin.Study of aperiodic information transmission in ensembles of excitable neurons［J］.Complex Systems and Complexity Science，2009，6（4）：66-70.

［12］于海涛，王江，刘晨，等.耦合小世界神经网络的随机共振［J］，物理学报，2012，61（6）：068702.

Yu Haitao，Wang Jiang，Liu Chen，et al.Stochastic resonance in coupled small-world neural networks［J］.Acta Physica Sinica，2012，61（6）：068702.

［13］龚振宇，庞全，范影乐.自适应随机共振的图像复原研究［J］.计算机工程与科学，2009，31（5）：46-49.

Gong Zhenyu，Pang Quan，Fan Yingle.The image restoration research by auto-adapted stochastic resonating［J］.Computer Engineering &Science，2009，31（5）：46-49.

［14］Higham D J.An algorithmic introduction to numerical simulation of stochastic differential equations［J］.SIAM Review，2001，43（3）：525-546.

［15］Chapeau-Blondeau F，Chambet N.Synapse models for neural networks：from ion channel kinetics to multiplicative coefficient［J］.Neural Computation，1995，7（2）：713-734.

On Synaptic Signal Transduction in a Dynamical Saturating Model

WANG Jin-guang
（Shandong Foreign Trade Vocational College，Qingdao 266100，China）

The synaptic signal transduction in a dynamical saturation neuron model is studied.At the pre-synaptic and post-synaptic stages，the evolution of neurotransmitter molecules in the synaptic cleft can be described by a dynamical saturation model.In the presence of noise，the signal transduction in this model is characterized by the ensemble-averaged correlation coefficient.The evolution of synaptic signal transmission is solved by the Milstein's high-order method of stochastic differential equation.The numerical result of the ensemble average correlation coefficient demonstrates the effect of noise-enhanced signal transduction in a single neuron model and an ensemble population of synaptic saturation neurons.Moreover，the noise-enhanced signal transduction effect is more visible by tuning the ratio of saturating current and the population of neurons.

neural synaptic model；correlation coefficient；signal transduction；noise enhancement

Q612；N945.12

A

1672-3813（2013）02-0059-04

2012-12-25

山东省自然科学基金（ZR2010FM006）

王金光（1976-），男，山东宁津人，硕士，讲师，主要研究方向为系统理论。

（责任编辑 耿金花）