保险市场中三寡头垄断的动态博弈模型研究
2013-09-28马军海
徐 伟,马军海
(天津大学管理与经济学部,天津 300072)
保险市场中三寡头垄断的动态博弈模型研究
徐 伟,马军海
(天津大学管理与经济学部,天津 300072)

考虑三寡头垄断的保险市场动态价格博弈模型。在模型中,一个寡头采取自适应决策,其余两个寡头采取有限理性决策,由此建立三寡头价格博弈微分方程模型。系统有唯一的Nash均衡点。并对该系统的稳定性和Hopf分岔的存在性进行研究。数值模拟结果证实了理论的准确性,并且展示了系统的动态行为。保险公司在考虑延迟的价格博弈的过程中,必须控制好延迟参数的值,并适当地降低自身价格调整速度,以使系统尽快稳定到平衡状态。
保险市场;寡头垄断;动态博弈;自适应;有限理性
0 引言
随着中国保险市场的发展,内资、外资保险公司的数量逐渐增加,虽然中国保险市场的垄断程度有所下降,但仍然处于寡头垄断阶段。多数文献是对保险市场寡头垄断竞争中的静态博弈研究,而动态博弈研究的文献则相对较少。韩树枫等[1]利用博弈论的知识来分析保险市场竞价,认为保险公司并不一定要通过最低价来占领市场,从而提出相应的竞价策略。姚洪兴等[2]将古诺模型应用到银行竞争领域中,并分析该模型中不动点的稳定性,得出各参数对模型稳定性的影响。潘玉荣等[3]提出了市场参与者具有不同理性层次的观点,寡头双方分别采用延时有限理性竞产决策和最优反应,从而建立基于不同理性的双寡头产量博弈模型。徐峰等[4]在双寡头广告博弈模型中引入延迟决策,分析了一方引入延迟决策,另一方为不考虑延迟的有限理性决策,并进一步分析延迟决策对系统的影响。E.M.Elabbasy等[5]建立了具有不同理性的三寡头离散模型,并对系统均衡点的稳定性条件进行了分析。H.N.Agiza等[6]对有限理性的Bowley模型进行了分析,研究了系统均衡点的存在性和稳定性,并对垄断中考虑延迟有限理性的Bowley模型进行研究。Zhang Jixiang等[7]对考虑有限理性的Bertrand模型进行研究,并分析价格调整速度对动态系统均衡点稳定性的影响。Chen Yuanyuan[8]和Xiaobing Zhou等[9]研究了具有时滞的微分方程模型,并分析系统的稳定性。高琴[10]用生态学的理论分析集装箱码头公司之间的竞争与合作,通过对Lotka-Volterra模型的改进,建立适当的非线性模型,研究无时滞和有时滞这两种情况下模型的稳定性和Hopf分岔情况。Woo-Sik Son等[11]研究一类金融系统的动态模型,并分析延迟系统的局部稳定性以及延迟对系统的影响。本文以保险市场作为研究背景,建立三寡头垄断的动态价格博弈模型。在一个寡头基于自适应决策、另两个寡头基于有限理性决策的情况下,对系统进行理论分析和数值模拟。根据数值模拟结果,总结出系统中相应参数的变化对系统稳定性的影响。
1 模型建立
目前中国的保险市场仍然是寡头垄断市场,所以很多文献都是在寡头垄断的前提下对其进行研究。通常对于企业的动态博弈研究都是在Cournot模型和Bertrand模型的基础上做出改进,以使该模型与实际情况更相符。但是大多数研究都是基于Cournot模型的,而且寡头企业主要是做的产量博弈。在现实生活中,许多企业都是通过价格竞争来占领市场份额的,所以在这些市场中对企业价格博弈的研究表现得尤为重要。
近年来,中国财产保险业发展迅速,取得了很大的成就,尤其在业务总量和保费收入等方面,中资财险公司保持着快速的发展势头。在2011年的中资财险公司综合竞争力排行榜上,人保股份、平安财产和太保财产已经连续4年保持在前3的位置。在这种背景下,可以将中资财险市场看成是一个三寡头垄断的保险市场。假设人保股份处于主导地位,采取自适应决策,而平安财产和太保财产则采取有限理性决策,在此背景下,可以做以下的模型建立和分析。
在一个三寡头垄断的保险市场中,各保险公司之间进行动态价格博弈。如果pi(t),i=1,2,3分别表示保险公司i对其自身产品制定的价格,qi,i=1,2,3分别表示各保险公司的产品需求量,那么各保险公司的逆需求函数为

其中,a,bi,gi,hi>0,i=1,2,3,a为市场最大需求量,bi为各企业的需求弹性,gi,hi表示的是其中两个保险公司产品的替代率。如果两保险公司无固定成本,ci>0,i=1,2,3分别为第i个保险公司的边际成本,那么可以假定3个保险公司的成本函数为式(2)的线性形式[3]:

因此,保险公司的利润函数可表示为
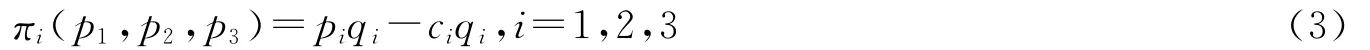
将式(1)代入式(3),得
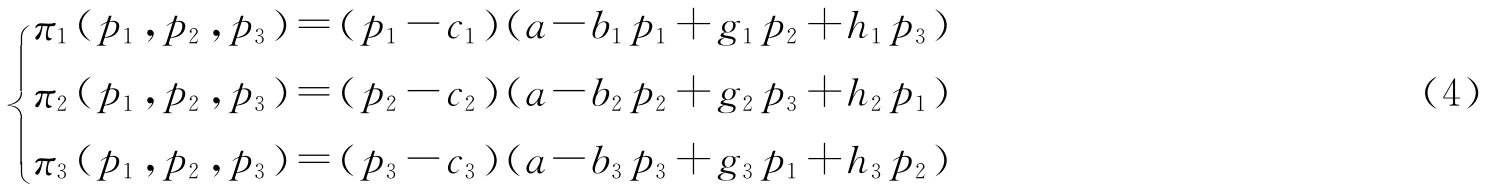
根据式(4),求得三寡头的边际利润为
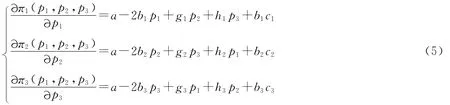
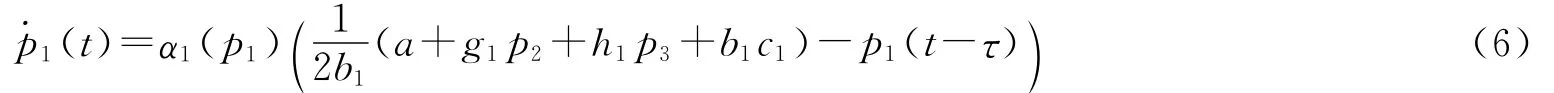
假设其余两个寡头采取的是有限理性决策,由于企业具有不完全的市场信息,所以为了将其利润最大化,企业在做出价格决策的时候可以考虑其边际利润情况。如果边际利润是正数,企业就决定提高产品价格;反之,降低产品价格。所以这两个寡头的价格调整的动态过程为
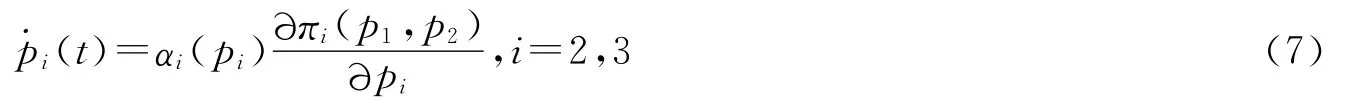
假设αi(pi),i=1,2,3是线性形式[7]的,即

其中,vi是一个正数,表示第i个保险公司的价格调整速度。
因此,综合式(6)、(7)和(8),可以得出保险公司价格决策的最终博弈模型为
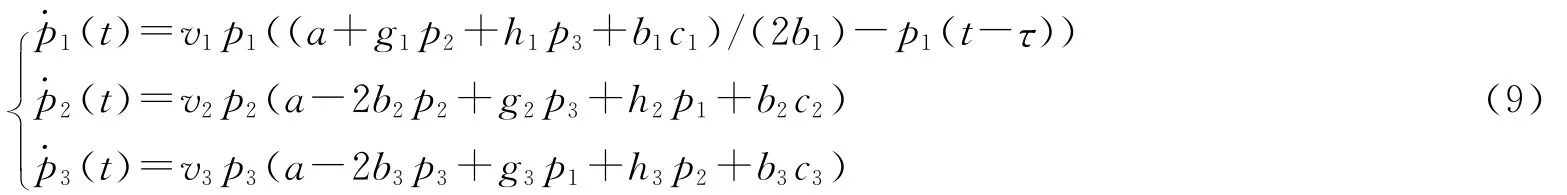
2 模型分析
基于经济模型本身的意义,均衡解应为非负解。对系统(9)进行求解,可以得到8个均衡点:
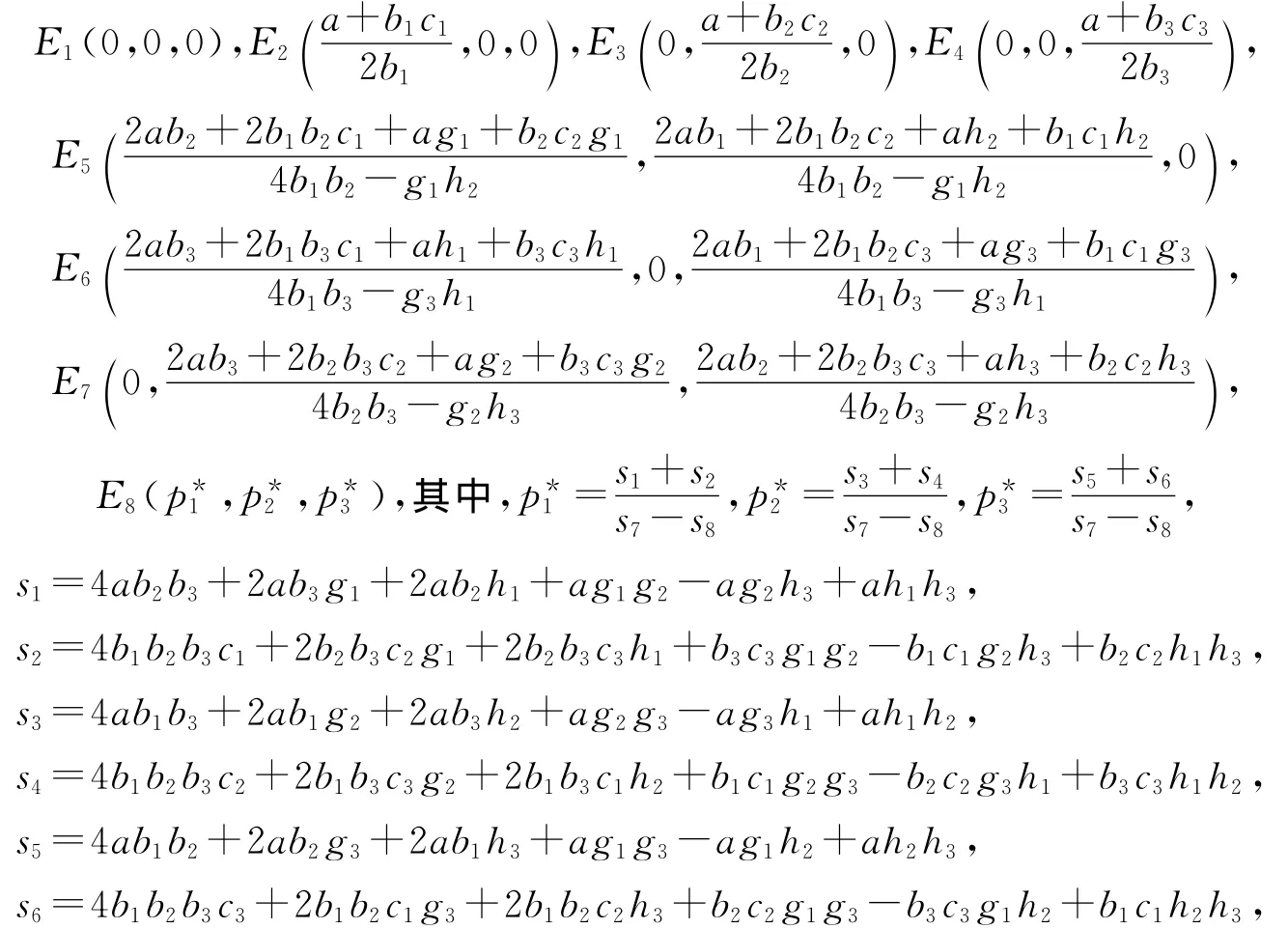
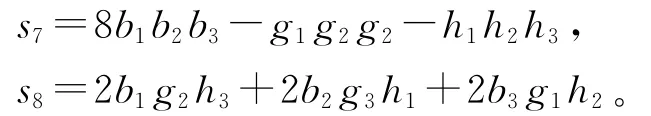
显然,E1,E2,E3,E4,E5,E6,E7,是系统(9)的边界均衡点,E8则是系统(9)唯一的 Nash均衡点。对于均衡状态E1(0,0,0),它表示3个企业最终的价格都为零,都将面临倒闭的危险。对于均衡状态E2,E3,E4,则表示只有一个保险公司在竞争中存活,其价格达到了只有其自身存在时的最优状态,其余两个保险公司的价格为零,都将面临倒闭的风险。对于均衡状态E5,E6,E7,则表示有两个保险公司可以经受住竞争的考验而存活,只有一个保险公司的价格为零。对于均衡状态E8(p,p,p),是指3个寡头通过竞争而达到的稳定状态,只有这个状态是博弈参与者希望的,因为在这个均衡下各企业都可以获得一定的市场份额,而不会退出市场竞争。
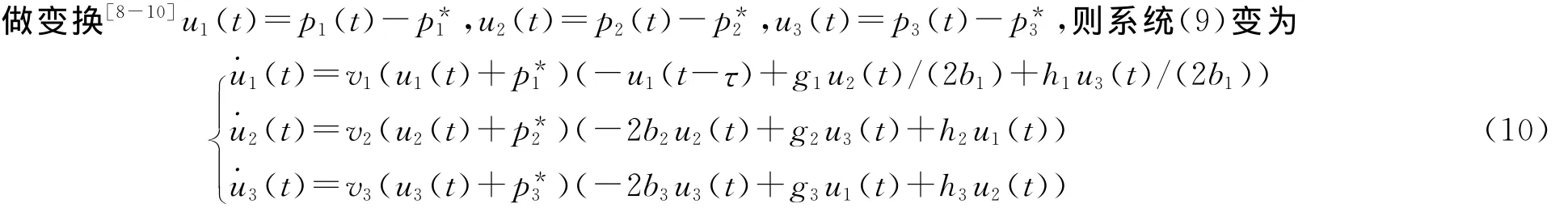
所以,研究均衡点E8的稳定性就转变为研究点(0,0,0)的稳定性。
系统(10)在u=0处的线性部分为
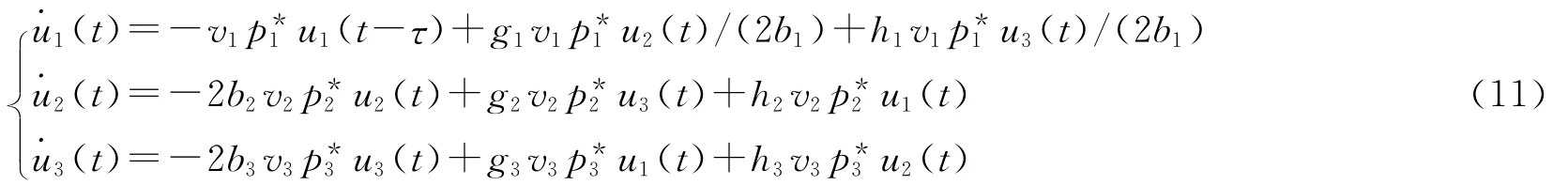
系统(11)的特征方程为
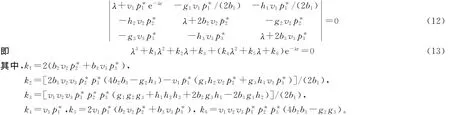
如果λ=iω(ω>0)是方程(13)的一个根,则
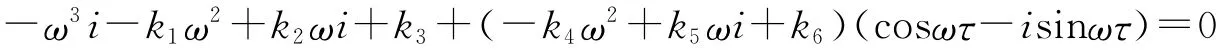
分离实部和虚部,有
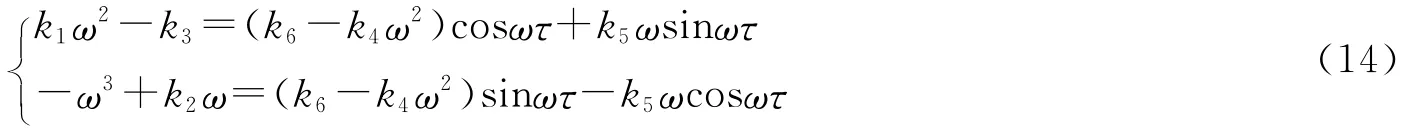
把方程(14)平方后相加,有
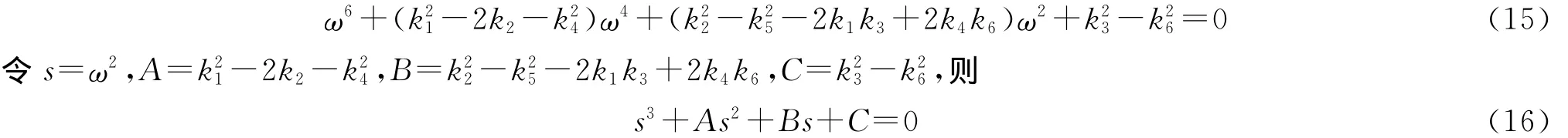
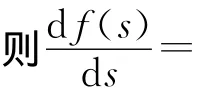
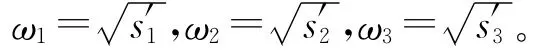
将ωk(k=1,2,3)代入方程(14),可以解得τjk
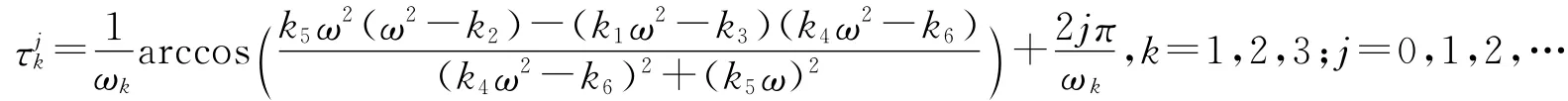
所以±iωk是特征方程(13)的纯虚根,并记τ0=min{τ0k},k=1,2,3。
当τ=0时,特征方程(13)变为

根据Routh-Hurwitz判据,如果

那么方程(17)的所有根都具有负实部。
综上所述,在式(18)成立的条件下,有下列结论:1)如果C≥0且Δ≤0,那么对于所有的τ≥0,系统(9)的均衡点E8是渐近稳定的;2)如果C<0或者C≥0,Δ>0,s1>0,f(s1)≤0,那么对于τ∈[0,τ),系统(9)的均衡点E8是渐近稳定的;3)如果2)中的条件成立,但是f′(s′k)≠0,k=1,2,3,那么当τ=τjk(j=0,1,2,…)时,系统(9)在均衡点E8处发生Hopf分岔。
综上所述,当系统参数满足一定条件时,将会产生周期解,而且随着延迟参数的不断增大,系统周期解运动的幅度也会越来越大。表现在现实情况中,各保险公司为了获得更多的利润,通过选择延迟参数的大小来不断改变自身的竞争策略,最终会使保险市场变得不稳定,从而博弈各方无法制定出合理的价格,其利润也就会受到影响。这种情形是所有保险公司都不愿意看到的,因此各寡头需要通过合理适当的竞争,来促进保险市场的快速发展,为保险市场提供良好的竞争环境。
3 数值模拟与分析
为了更好地反映系统的动态行为,对系统进行数值模拟与分析。
当第一家保险公司采取自适应决策,其余两家采取有限理性决策时,取市场参数a=5,b1=3.8,b2=3.5,b3=3.1,g1=0.4,g2=0.5,g3=0.6,h1=0.45,h2=0.55,h3=0.65。3个保险公司各自的边际成本为c1=0.001 6,c2=0.001 4,c3=0.001 2。3个保险公司自身产品价格的初值分别为p1(0)=0.5,p2(0)=0.4,p3(0)=0.3,价格调整速度为v1=v2=v3=0.5。此时,可以计算出延迟参数的临界值τ0=4.128 8,系统的均衡解为E8(0.760 5,0.844 0,0.969 1)。通过Matlab软件对系统(9)进行数值模拟,依次取τ=3.5,4,4.128 8,4.3,模拟结果如图1~4所示。从这4幅图中可以看出,当τ<τ0时,系统最终会稳定到平衡状态。随着τ的增大,系统稳定到平衡状态所需的时间也在增加。当τ=τ0时,系统发生Hopf分岔,出现周期解。随着τ的增大,系统周期运动的幅度也越来越大。
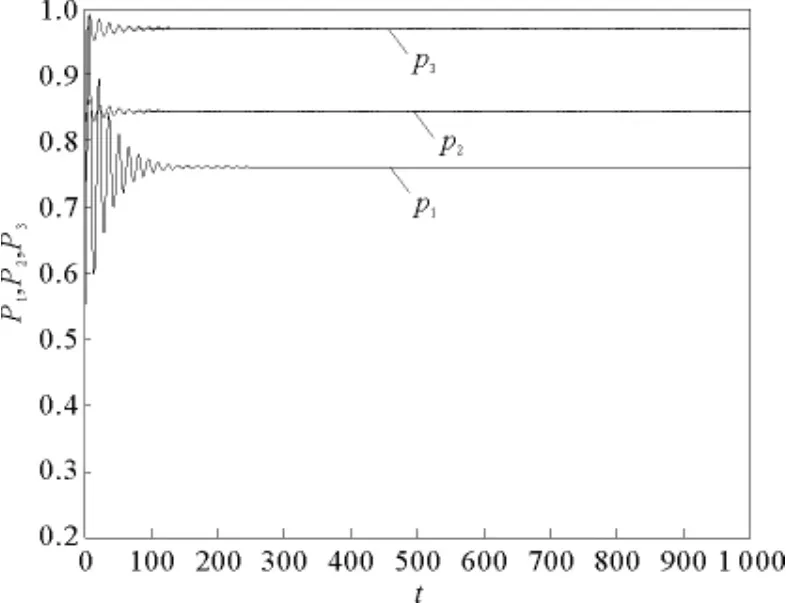
图1 τ=3.5,系统稳定到平衡状态Fig.1 τ=3.5,the system is stable
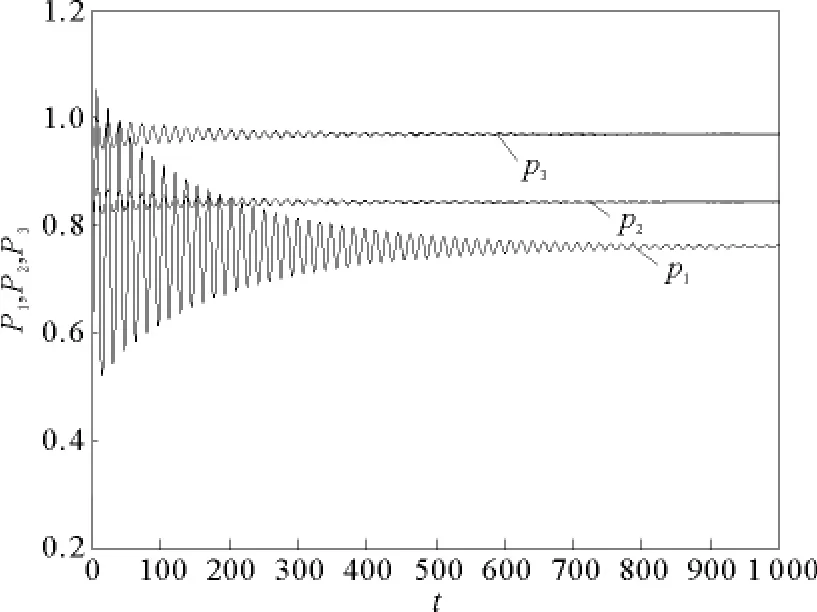
图2 τ=4,系统稳定到平衡状态Fig.2 τ=4,the system is stable
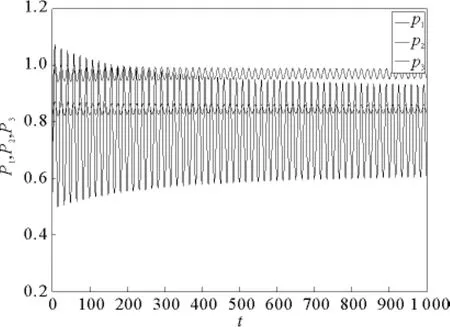
图3 τ=4.128 8,系统发生Hopf分岔Fig.3 τ=4.128 8,Hopf bifurcation occurs
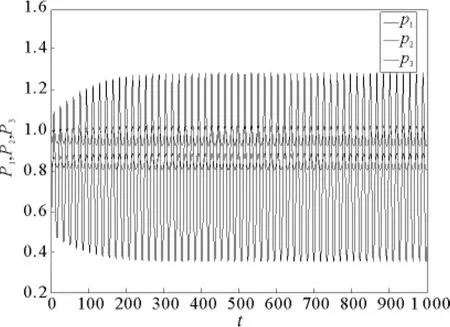
图4 τ=4.3,系统周期运动幅度增大Fig.4 τ=4.3,the amplitude of periodic motion increases
从数值模拟结果可以看出,对于采取自适应决策的保险公司来说,要尽量减小其所考虑的τ值,从而使系统尽快达到稳定状态。保险公司必须根据自身的经营情况和产品价格的变化作出调整,从而使产品的价格尽快达到稳定状态,避免整个保险市场的价格紊乱现象。这样既可以提高保险公司的服务质量和声誉,又可以促进保险市场的平稳发展。如果保险公司所考虑的τ值过大,系统最终将不会稳定到平衡状态,而会发生Hopf分岔,并产生周期解。这对于保险公司自身的经营决策和其它相关部门的发展,将产生无法估计的不良影响。因此,如果保险公司要采取自适应决策,就必须减小τ值,即对市场价格作出迅速的反映。这样各保险公司在进行价格竞争的同时,也能够共同发展,对保险市场有着举足轻重的正面影响。
假设采取自适应决策的保险公司改变自身的价格调整速度,依次取v1=0.55,v1=0.6,并保持其它参数的值不变。对系统(9)进行数值模拟,结果如图5和图6所示。

图5 τ=3.5,v1=0.55,系统大约在t=450时稳定到平衡点Fig.5 τ=3.5,v1=0.55,the system will be stable at t=450
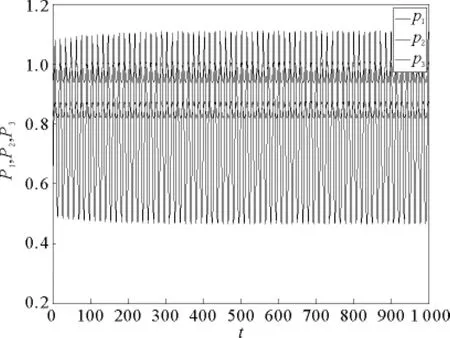
图6 τ=3.5,v1=0.6,系统出现周期解Fig.6 τ=3.5,v1=0.6,the periodic solution of the system occurs
比较图1、图5和图6,可以发现当τ=3.5时,随着价格调整速度v1的增加,系统稳定到平衡点所需的时间也在增加,增加到一定程度系统就会出现Hopf分岔,从而产生周期解。在实际的保险市场中,需求函数以及各自的边际成本都是相对确定的,价格调整速度就成为一个企业追求利润最大化的重要策略。随着该策略的开始实施,系统起初是稳定的,但是价格调整速度越来越大,系统就会变得不稳定。因此,保险公司必须控制好自身的价格调整速度,以便系统尽快稳定到平衡点,有利于各项经营决策的实施。保险公司为了获得正常利润,既要避免因价格调整速度过小而被市场淘汰,也要避免因价格调整速度过大而使市场变得不稳定所导致的整个保险市场的混乱。
4 结论
本文建立了保险市场中三寡头垄断的动态价格博弈模型,在博弈过程中,一方采取自适应决策,另外两方采取有限理性决策。通过对微分方程模型的理论分析和数值模拟,我们知道保险公司在价格博弈的过程中,如果采取自适应决策而考虑τ时刻之前的价格,就需要适当地减小τ的值,以缩短系统稳定到平衡点所需的时间。另外,各保险公司都需要控制好自身的价格调整度,不能一味地加快调整速度而忽略由此带来的负面影响。因此,各保险公司必须控制好系统中自身的参数,从而健康稳定地发展,并为整个保险市场带来益处。
[1]韩树枫,丁家兴.中国保险市场价格竞争的博弈分析[J].内蒙古科技与经济,2006(16):37-38.
Han Shufeng,Ding Jiaxing.Analysis of price game in China’s insurance market[J].Inner Mongolia Science &Technology and Economic,2006(16):37-38.
[2]姚洪兴,王海平.商业银行竞争博弈模型的复杂性分析[J].统计与决策,2007(21):55-57.
Yao Hongxing,Wang Haiping.Complexity of the game model of commercial banks’competition[J].Statistics and Decision,2007(21):55-57.
[3]潘玉荣,贾朝勇.不同理性双寡头博弈模型的复杂性分析[J].复杂系统与复杂性科学,2007,4(2):71-76.
Pan Yurong,Jia Chaoyong.Complex dynamics analysis for a duopoly game with heterogeneous players[J].Complex systems and complexity science,2007,4(2):71-76.
[4]徐峰,盛昭瀚,姚洪兴,等.延迟决策对一类双寡头广告博弈模型的影响分析[J].管理科学学报,2007,10(5):1-10.
Xu Feng,Sheng Zhaohan,Yao Hongxing,et al.Study on a duopoly advertising model with delayed decisions[J].Journal of Management Sciences in China,2007,10(5):1-10.
[5]Elabbasy E M,Agiza H N,Elsadany A A.Analysis of nonlinear triopoly game with heterogeneous players[J].Computers and Mathematics with Applications,2009,57(3):488-499.
[6]Agiza H N,Hegazi A S,Elsadany A A.The dynamics of Bowley's model with bounded rationality[J].Chaos,Solitons &Fractals,2001,12(9):1705-1717.
[7]Zhang J X,Da Q L,Wang Y H.The dynamics of Bertrand model with bounded rationality[J].Chaos,Solitons &Fractals,2009,39(5):2048-2055.
[8]Chen Y Y,Song C M.Stability and Hopf bifurcation analysis in a prey-predator system with stage-structure for prey and time delay[J].Chaos,Solitons &Fractals,2008,38(4):1104-1114.
[9]Zhou X B,Wu Y,Li Y,et al.Stability and hopf bifurcation analysis on a two-neuron network with discrete and distributed delays[J].Chaos,Solitons &Fractals,2009,40(3):1493-1505.
[10]高琴.港口产业集群的复杂性研究[D].天津:天津大学,2009.
Gao Qin.The research of the complexity of port industrial clusters[D].Tianjin:Tianjin University,2009.
[11]Woo-Sik Son,Young-Jai Park.Delayed feedback on the dynamical model of a financial system[J].Chaos,Solitons &Fractals,2011,44(4/5):208-217.
Study on the Dynamical Model of a Triopoly Game in Insurance Market
XU Wei,MA Jun-hai
(Tianjin University,College of Management and Economics,Tianjin 300072,China)
We consider the dynamical model of a triopoly price game in insurance market.In this model,one makes adaptive decision,the other two make decision with bounded rationality,then the differential equation model of triopoly price game is obtained.The system has only one Nash equilibrium.The stability and the existence of Hopf bifurcation of the system are studied.Numerical simulation results have further confirmed the accuracy of the theory and shown the dynamical behavior of the system.The insurance companies make decision in the price game with delay,they must choose appropriate value of the delayed parameter and decrease the speed of price adjustment.The system will become stable as soon as possible.
insurance market;duopoly;dynamical game;adaptive;bounded rationality
F224;N949
A
1672-3813(2013)02-0052-07
2012-05-30
徐伟(1987-),男,江苏泰州人,硕士研究生,主要研究方向为管理、经济与金融系统复杂性。
(责任编辑 耿金花)
