多孔介质孔隙尺度下不可压缩流体流动特性SPH模拟

李 维 仲， 赵 月 帅， 宋 永 臣

（大连理工大学 海洋能源利用与节能教育部重点实验室，辽宁 大连 116024）

0 引 言

在自然界和很多工业应用中，都包含了多孔介质内流体流动问题，如石油开采、地下水净化和流化床等领域.因此，深入了解在不同工况下，流体在多孔介质中的流动特性有着重大的实际意义.在实际工程中，流体在多孔介质内流动问题可以用达西定律进行描述，然而达西定律是一个基于宏观观测的实验定律，流体和多孔介质之间复杂的相互作用只能体现在一个宏观的统计参数k之中.因而，要详细研究这个参数，了解多孔介质具体构造对k的影响，发展一种新的能够在孔隙尺度下直接高效地模拟流体在复杂多孔介质中流动细节的数值模拟方法是非常必要的.

然而，采用传统的数值模拟方法，如有限元法、有限体积法等，模拟多孔介质内流体流动问题比较困难，在处理复杂的孔隙几何结构、多尺度、多相流动等问题时，都需要额外的处理技巧，同时容易出现精确度不高和数值稳定性较差等问题.值得一提的是，近年来发展非常快的格子Boltzmann方法（LBM）也常被应用于孔隙尺度下多孔介质内流动问题的研究.LBM是基于玻尔兹曼方程，介于微观流体分子动力学模型和宏观连续介质模型之间的介观方法，它既能捕捉到流体的微观特性，又能再现流体的宏观流动特性.在处理复杂边界问题时，LBM具有极大的优势，因此它是一种可以用来模拟具有任意几何边界系统（例如多孔介质）的非常有效的模拟方法.与有限差分方法等相比，LBM算法简单、易于程序化处理、计算效率高和具有天然的并行性，可以在计算机或者集群上运行，减少了计算代价和计算时间.但是，LBM仍然是一个基于网格的方法，在多尺度问题中，如果计算区域复杂，尤其是在解决具有大畸变、运动物质交界面、变形边界以及自由表面问题时，容易产生网格扭曲与网格重构问题.

一个可以替代LBM的方法是光滑粒子动力学（SPH）方法［1］.SPH 方法是一种无网格粒子方法，最初主要用于解决天文学问题［2－3］.经过数十年的发展，它已经广泛应用于不同领域内的计算流体力学问题.Monaghan［4］对SPH方法应用于流体力学的计算做了一系列的研究.Morris等［5］采用SPH方法研究了不可压缩流动问题和多孔介质中的流体流动问题，Zhu等［6－8］应用 SPH 方法模拟了孔隙尺度下流体的流动和扩散问题.

与基于网格的数值模拟方法相比，SPH方法主要具有以下两方面的优势［9］：一是它的物理意义简单明确.通过添加成对的粒子间相互作用，只需更改少量的代码，即可将复杂的物理和化学变化包含在SPH模型中.因为总粒子数在模拟中保持恒定，同时相互作用是对称的，质量、动量和能量方程守恒性好，而且使用者可以简单地在一个指定区域内添加更多粒子从而得到更加精确的结果.二是可以相对简单地处理复杂几何边界问题.该方法仅仅处理一些离散的点，在粒子的运动过程中，可以通过粒子和骨架结构的相互作用反映固体边界的影响，无需进行额外的处理，因此它非常适用于研究复杂几何边界问题.

本文采用SPH方法，在孔隙尺度下模拟多孔介质内不可压缩流体流动，研究流体流动的细节及其特性.

1 光滑流体动力学基础

SPH方法是一种基于插值理论的无网格拉格朗日方法.在SPH方法中，系统状态和运动由一系列随机分布的离散粒子来表示.每一个粒子都具有质量m、密度ρ、速度v，以及其他的流体性质.通过使用一系列任意分布的节点（或者粒子）来求解积分方程组或者偏微分方程组，从而得到精确稳定的数值解.

在SPH方法中，函数f（r）的积分近似式为

式中：r为粒子坐标；h为光滑长度；W（r－r′，h）为核函数.

相应的函数在某一插值点i的粒子近似式为

式中：求和操作应用于核函数在插值点i支持域内的所有N个粒子；Wij＝W（ri－rj，h），为核函数.核函数选取应用最广泛且精度较高的五次光滑核函数：

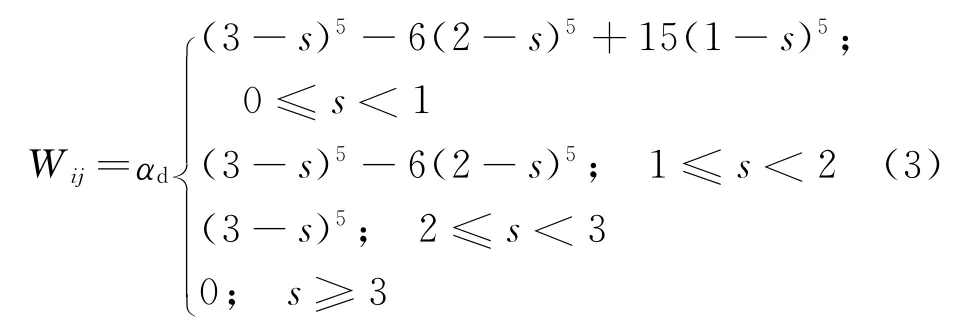
SPH方法中的控制方程组是不可压缩流体N－S方程组的特殊离散形式，其中，连续方程为

动量方程：

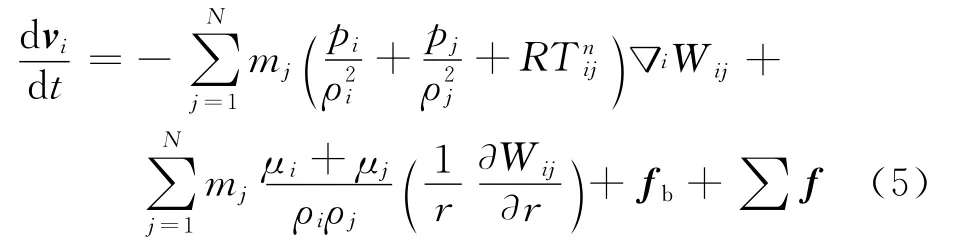
式中：p为压力；μ为流体动力黏度；fb为单位质量体积力；∑f为粒子与多孔介质的相互作用力为一个很小的人工力，用于抑制张力不稳定性［10］，其中

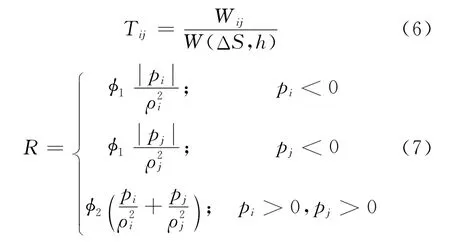
式中：1＝0.2，2＝0.05，n＝3；ΔS一般取初始粒子间距.

通过引用人工压缩方法来处理不可压缩流体，采用的状态方程为

粒子按照以下形式运动：

为了实现无滑移边界条件，采用一种反射对称布置的虚粒子来模拟壁面.这些虚粒子具有与相对应的实粒子相同的密度和压力，但速度方向相反.这些虚粒子在每个计算步中由对应的实粒子对称产生.为阻止粒子穿越边界，每个边界上的虚粒子都添加了一个类似于计算分子力时所使用的Lennard－Jones排斥力，如下所示：

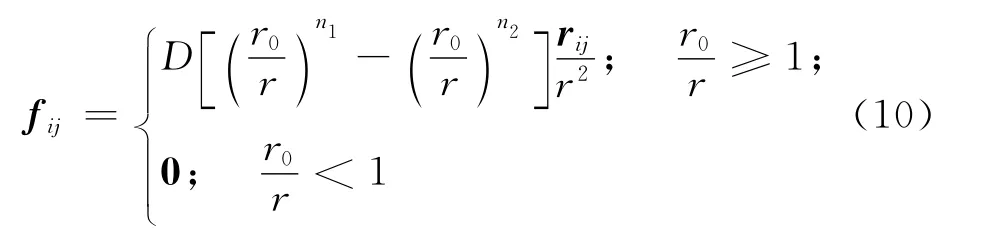
式中：n1＝12，n2＝4；D为由具体问题所定的参数，一般取与速度的最大值的平方相等的量级；r0为截止半径.

本文采用周期性边界条件模拟无限长通道中的流体流动问题.这意味着在粒子运动过程中，当粒子即将离开指定区域穿越边界时，有一个具有相同流体性质（速度和密度）的新粒子在另一个边界产生并进入计算区域，进而保证计算区域的粒子总数不变.

2 SPH方法的数值验证

用经典算例Poiseuille流和Couette流对计算方法进行验证，并将模拟结果和解析解进行对比.本文中，计算域为0.001m×0.001m，流体为水，密度ρ＝1×103kg／m3，运动黏度ν＝1×10－6m2／s，为了减少计算误差，使流体流动的特征速度接近mm／s的数量级，Poiseuille流中的水平方向单位质量体积力fb＝0.02N／kg，Couette流中的顶边运动速度v0＝2.5×10－3m／s，粒子数量为40×40，光滑长度取定值，为粒子初始间距的1.1倍，时间步长取为1×10－4s.

图1 Poiseuille流速度分布Fig.1 Velocity profiles for the Poiseuille flow

图2 Couette流速度分布Fig.2 Velocity profiles for the Couette flow

在经历6 000步计算后，模拟达到稳定状态.图1和2分别给出了Poiseuille流与Couette流，由SPH方法和级数求解法（解析法）得到的在t＝0.01、0.1s和最终状态t＝∞时的速度分布图，可见SPH方法所得到的结果和解析法所得到的结果相当吻合，相对误差在1%以内.

3 SPH方法在多孔介质中流体流动的应用

3.1 模拟规则多孔介质中流体流动

计算域为0.001m×0.001m，初始粒子分布为64×64，x和y方向均采用周期性边界条件，流体为水，运动黏度和密度分别为ν＝1×10－6m2／s和ρ＝1×103kg／m3，为了减少计算误差，使流体流动的特征速度接近mm／s的数量级，水平方向单位质量体积力取为fb＝0.2N／kg.本文中，分别采用方柱和圆柱两种骨架结构来构造规则多孔介质，方柱边长和圆柱直径分别为0.5mm和0.564mm，两种多孔介质的孔隙率均为0.75.

同时采用SPH方法和FEM对稳态不可压缩流体流动进行模拟，得到的水平速度分布如图3所示，曲线a和曲线b分别表示在x＝l／2和出口处的水平速度分布.两种模拟方法所得到的结果吻合良好.

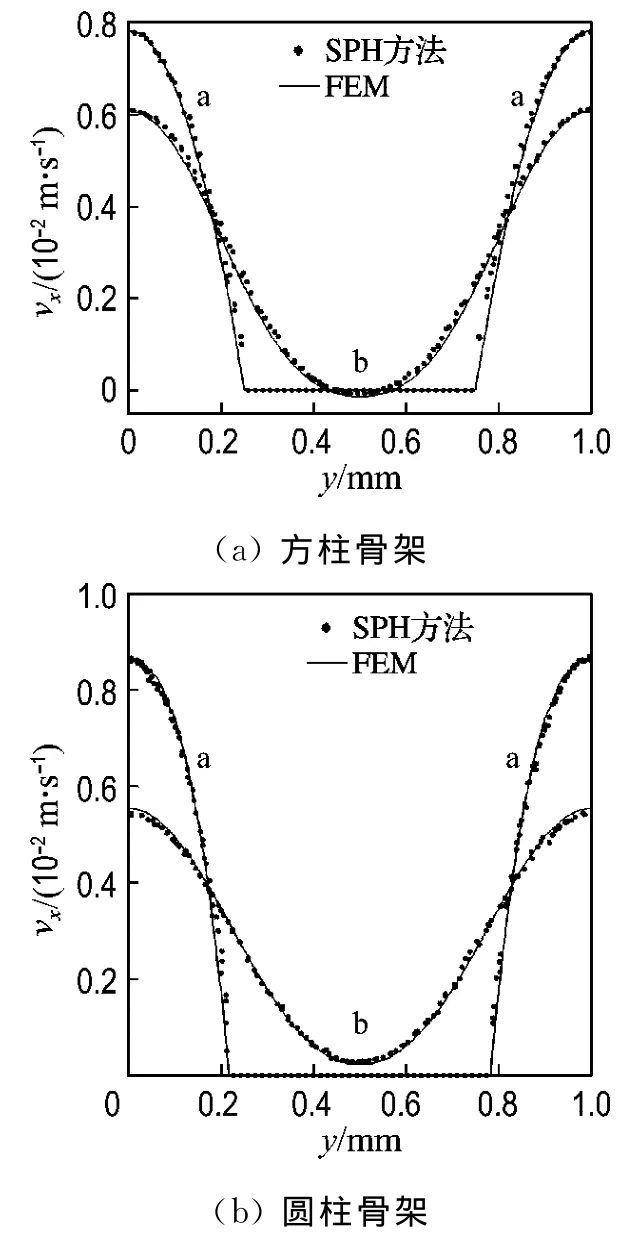
图3 多孔介质中SPH方法和FEM得到的水平速度分布比较Fig.3 Comparison of horizontal velocity obtained by SPH method and FEM in porous media

3.2 模拟贝雷岩心模型与人工随机多孔介质中的流体流动

计算域为0.001m×0.001m，初始粒子分布为64×64，x和y方向均采用周期性边界条件，流体为水，运动黏度和密度分别为ν＝1×10－6m2／s和ρ＝1×103kg／m3.根据规则多孔介质的模拟结果，水平方向单位质量体积力分别取为fb＝0.2、0.4、0.6、0.8N／kg.在本文中，采用两种不同的多孔介质模型，第1种模型是基于贝雷岩心的核磁成像图像数据构建的，图4为由核磁共振成像仪得到的自旋密度图及将成像数据二值化处理后得到的图像.考虑计算效率，只选取其中的局部区域作为研究对象，考察其孔隙结构内部的流体流动情况，所选取的岩心模型如图5所示.

图4 贝雷岩心自旋密度图像与二值化图像Fig.4 Spin density image and binary image of Berea sandstone

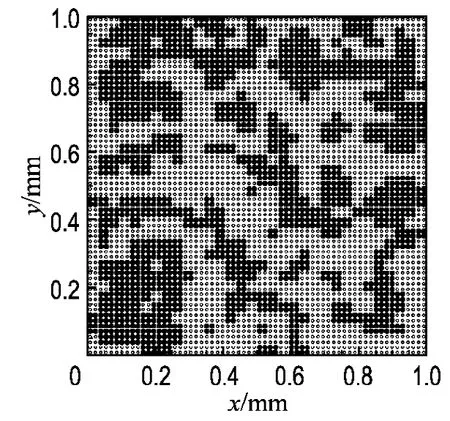
图5 贝雷岩心模型（孔隙率为0.577）Fig.5 Berea sandstone model（porosity is 0.577）

第2种模型为采用随机方法，以同尺度的圆柱为基元生成的多孔介质模型，其孔隙率与贝雷岩心模型相同，如图6所示.

多孔介质的渗透率由下式确定：

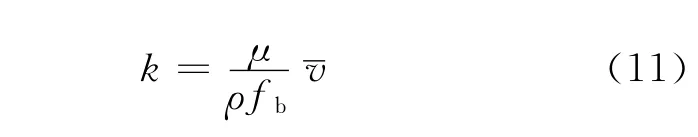
图6 人工随机多孔介质模型（孔隙率为0.577）Fig.6 Artificial random porous media model（porosity is 0.577）

图7 表示稳态流动时，流体平均速度和单位质量体积力fb之间的关系.可以看出模拟结果呈现了很好的线性关系.根据图7（a）、（b）中拟合直线的斜率和流体物性，由式（11）计算得到贝雷岩心模型和人工随机多孔介质的渗透率分别为k1＝2.74×10－11m2和k2＝4.64×10－10m2.这与通过达西定律所得到的预期结果相符.

图7 平均流体速度和单位质量体积力的关系Fig.7 Average flow velocity versus body force per unit mass

4 结 论

本文利用SPH方法模拟了经典的Poiseuille流和Couette流，对所开发的SPH计算程序进行了验证，并分别利用SPH方法和FEM研究了流体在两种不同的规则多孔介质中的流动特性.在低速流动下，SPH方法计算结果和FEM的计算结果都非常一致，说明SPH模型可以在微观尺度下直接模拟多孔介质内流体流动的详细情况.最后，研究了流体在基于真实的贝雷岩心获得的多孔介质模型和以同尺度的圆柱为基元随机构造的多孔介质模型内的流体流动情况.结果表明，该SPH模型可以用于研究多孔介质内流体流动问题，能够很好地模拟多孔介质的微观结构对多孔介质内流体流动特性的影响，可以很容易地迁移应用于任意形状和大小的固体骨架结构之中的流体流动问题.模拟得到的平均流体速度和单位质量体积力有着很好的线性关系，符合通过达西定律所得到的预期结果.

［1］LIU Gui－rong，LIU Mou－bin.Smoothed Particle Hydrodynamics— A Meshfree Particle Method［M］.Singapore：World Scientific，2004.

［2］Gingold R A，Monaghan J J.Smoothed particle hydrodynamics — Theory and application to nonspherical stars ［J］.Monthly Notices of the Royal Astronomical Society，1977，181：375－389.

［3］Lucy L B.A numerical approach to the testing of the fission hypothesis ［J］.The Astronomical Journal，1977，82：1013－1024.

［4］Monaghan J J.Smoothed particle hydrodynamics［J］.Reports on Progress in Physics，2005，68（8）：1703.

［5］Morris J P，Fox P J，ZHU Yi.Modeling low Reynolds number incompressible flows using SPH［J］.Journal of Computational Physics，1997，136（1）：214－226.

［6］ZHU Yi， Fox P J.Smoothed particle hydrodynamics model for diffusion through porous media ［J］.Transport in Porous Media，2001，43（3）：441－471.

［7］ZHU Yi，Fox P J.Simulation of pore－scale dispersion in periodic porous media using smoothed particle hydrodynamics ［J ］.Journal of Computational Physics，2002，182（2）：622－645.

［8］ZHU Yi，Fox P J，Morris J P.A pore－scale numerical model for flow through porous media［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1999，23（9）：881－904.

［9］胡晓燕.计算流体力学中的SPH方法和 MLSPH方法研究［D］.北京：中国工程物理研究院，2006.HU Xiao－Yan.Research on SPH and MLSPH method in computational fluid dynamics ［D］.Beijing：China Academy of Engineering Physics，2006.（in Chinese）

［10］Monaghan J J.SPH without a tensile instability［J］.Journal of Computational Physics，2000，159（2）：290－311.