力梯度辛方法在圆型限制性三体问题中的应用*

陈云龙 伍歆

(南昌大学理学院,南昌 330031)

(2013年1月11日收到;2013年3月27日收到修改稿)

1 引言

辛积分器[1]和流形改正方法[2,3]都属于几何积分算法[4],两者同样都能确保能量积分误差在长时间积分中没有长期变化,但差别在于前者能够保持Hamilton系统的辛结构,而后者却不能.辛方法因具有这两个优点,从而成为求解Hamilton系统长期演化的最佳数值积分方法,它已在分子动力学[5]、量子力学[6-8]、声波[9]、等离子体[10]、太阳系动力学和相对论天体物理[11-14]等领域得到广泛应用.

辛积分器分为显式[15]和隐式[1]两种形式.有时也会用到它们的混合形式[11-14,16-18],但这种混合型本质上还是归结于隐式方法.显辛方法比隐辛方法具有计算效率方面的优势,故通常受到学者们的关注.应当注意它的使用要求Hamilton至少要分解成两个可积部分,例如由动量和坐标分别组成的动能与势能就是一种Hamilton分解形式.二阶Verlet辛积分器[4]尽管是这种分解形式下的一种简单的显辛方法,但在辛方法研究中却发挥重要作用,被认为是获得高阶或高精度辛积分算法的基础.直接消去其三阶截断误差项,若按不对称组合方式可以得到三阶辛方法[15];若按对称组合方式则可以取得四阶Forest-Ruth辛积分器[19],还能得到Yoshida高阶辛积分器[20].当Hamilton分解成主要的未受摄部分和次要的摄动部分并且两部分均可积时[21],Verlet辛积分器的三阶截断误差中有一项会比另一项大很多.若将该阶甚至各阶截断误差中的主要项消去但次要项仍保留,则得到类高阶(pseudo-high-order)辛方法[22,23],还可以取得辛校正器[24].在太阳系动力学中,这种摄动分解形式及构造的有关算法与动-势能分解的同阶算法来比显著提高了数值精度.应该指出摄动分解情形下Verlet辛积分器的三阶截断误差中的所谓次要项当实施动-势能分解时与另一项不再有明显的主次之分,亦即没有很大的量级差异,将会在算法构造中很有用,它本质上就是力的梯度.Ruth[15]正是认识到这一点,把它加入势能中再与动能组合求解构造了一个三阶力梯度辛方法.沿着该思路,可以设计一系列高阶力梯度辛方法[25-30]及其截断误差各项系数平方和最小的最优化型算法[31,32].不超过四阶的力梯度辛方法各组合系数可以全为正数,意味着积分过程中的每一子步都用正步长,这有益于求解不可逆系统.大量文献[25-32]表明力梯度辛方法在Kepler二体问题、摄动Kepler二体问题、太阳系N体问题、分子动力学多粒子问题、量子力学薛定谔方程以及H´enon-Heiles系统等模拟中比同阶非力梯度辛方法要好一到几个数量级精度,并且最优化型总要优于没有经过优化处理的算法.类高阶辛方法、辛校正器和力梯度辛方法实际上都是直接将误差项中的某些部分提取出来加入组合来构造新的算法,以便使所得算法误差里不再含有该提取部分,从而改善数值精度.从这一角度来看,它们均含有误差校正的意思.

考虑到四阶力梯度辛方法与非力梯度Forest-Ruth辛积分器来比具有精度好的优点,文献[26]将其应用于求解惯性坐标系下的圆型限制性三体问题.这里第三个小天体受到两主天体所给引力的梯度连同引力被一起用来构造算法.这种处理是合理的,因为惯性系下的第三体受力在物理上是非常清晰的.然而,圆型限制性三体问题的研究大都在旋转坐标系下进行,这时第三体除受到两主天体引力外还受到旋转坐标系所产生的非惯性力,使得第三体受力变得复杂起来,进而导致力梯度算法的应用变得困难,因为我们不清楚力梯度究竟是哪种力的梯度,即是关于引力的梯度还是非惯性力的?也许有人认为应当是针对引力与非惯性力的合力来实施梯度运算,但这样会使引力与非惯性力对应的Hamilton之和不可积,也就是显辛方法不再适合,故显辛方法在实际应用中需要将引力与非惯性力分开计算.因此,我们不直接从第三体受力分析出发而是改由有关Lie算子运算来探讨力梯度辛方法是否适合求解旋转坐标系下的圆型限制性三体问题.这是本文的一个主要目的.具体来说,通过评估比较四阶力梯度辛方法[25]、最优化四阶力梯度辛方法[31]和Forest-Ruth辛方法[19],我们希望找到适合求解旋转坐标系下的圆型限制性三体问题精度最好的辛积分器.然后,利用所挑出的算法计算两邻近轨道的Lyapunov指数[33]和快速Lyapunov指标[34],达到完全确保高精度辛方法能够贯穿于这些混沌指标计算的全过程,可为正确揭示系统动力学定性性质服务.

2 算法描述

设动能T(p)是关于n维动量p的二次型T(p)=p2/2,而势能V(q)仅是n维坐标q的函数,它们组成的Hamilton函数为

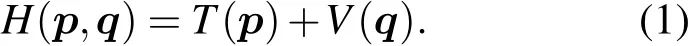
依次定义T和V的Lie导数算子为

上式中,Ti=∂/∂pi,Vi=∂/∂qi,以下类同.Lie导数A分别作用于坐标qi和动量pi,实际上就是关于坐标和动量的普通导数,即q˙i=Aqi=Ti,p˙i=Api≡0,表明A仅仅对位置坐标有作用,故称为位置型算子;B自然称为动量型算子,它对pi作用就得到力或加速度.利用这两个算子可以构造二阶Verlet辛积分器[4]

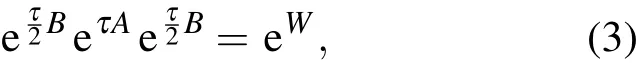
这里,τ为步长,而

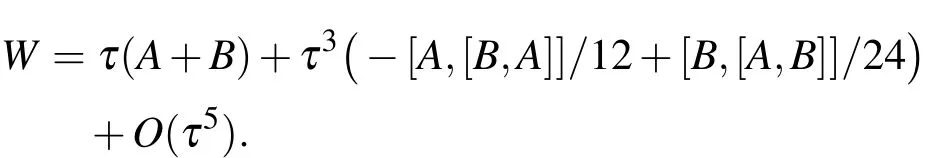
在三阶截断误差中,互逆子

容易验证

但

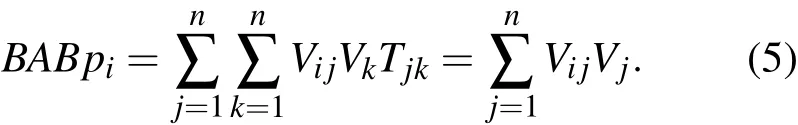
于是,可得

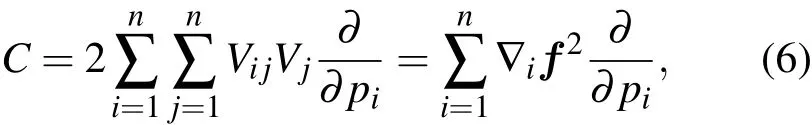
其中,力 f=(-V1,···,-Vn).显然,C 就是力梯度算子,与B属于同类的动量型算子.

既然如此,可将截断误差中的C提取出来并和B等同看待再跟A组合构造一类更高阶算法,称为力梯度辛方法.例如,一个简单四阶力梯度辛方法[25]为

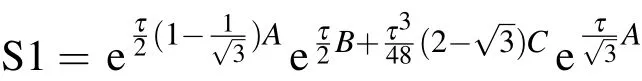
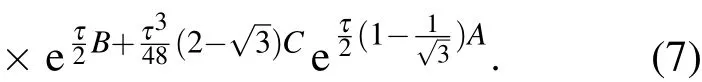
如还要求五阶截断误差各项系数的平方和最小,则得一个最优化四阶力梯度辛方法[31]

其中,各步进算子的系数约定如下：

当不考虑C加入组合式中,则是通常的辛方法.常见的例子就是四阶Forest-Ruth辛积分器[19]

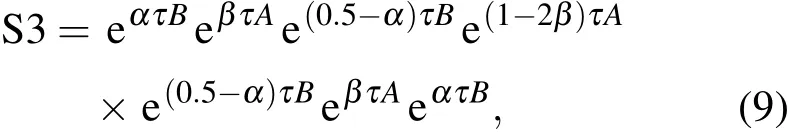
3 圆型限制性三体问题

本节致力于力梯度型算法在旋转坐标系下的圆型限制性三体问题中的具体实现,并以非力梯度型为参考评估这些算法的精度优劣,最后利用所挑选的精度最佳算法计算一些混沌指标.

3.1 物理模型

经典平面圆型限制性三体问题[35]揭示的是第三个无限小质量天体在做匀速圆周运动的两主天体的引力作用下的运动情形.约定两主天体总质量为1,质量为m1=1-µ的一体位于质心旋转坐标系内的x轴上的点(-µ,0),而质量为m2=µ≤1/2的另一体位于点(1-µ,0).这样两主天体固联在x轴上始终保持1不变,但它们以匀角速度1做圆运动,即x轴围绕原点以匀角速度1旋转并不受小天体引力的影响.在这两主天体的引力作用下小天体的坐标q=(x,y)和动量p=(px,py)演化以无量纲Hamilton函数表为

力函数U(x,y)具有如下形式

该系统具有正则方程

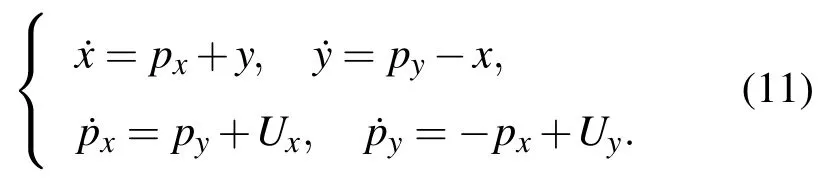
容易验证存在Jacobi常数

显辛方法的应用并不针对整个系统(10)或(11)而是将其分离成两个可积部分分别求解.系统(10)的一种分解形式可以是如下的“动能T”和“势能V”两部分

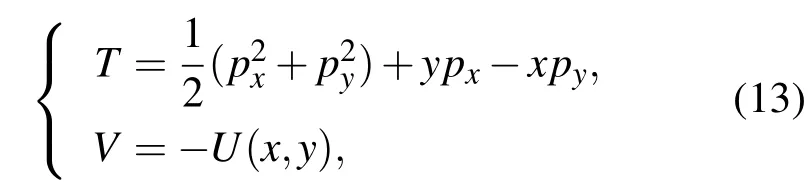
势能V来自于两主天体施加给小天体的引力作用部分,而ypx-xpy是因旋转坐标系为非惯性系而给小天体运动附加的影响部分.

从(13)式来看,T不是动量p的二次型,这使得力梯度算法的应用似乎遇到了困难,下面力图解决这一问题.

3.2 算法实现

由于T不是动量p的严格二次型,故其Lie导数算子A不再有方程(2)形式,而是由位置型算子变为动量与位置混合型算子

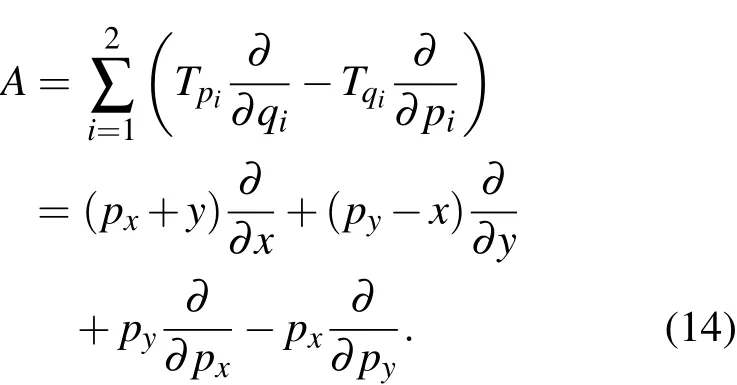
它作用于坐标和动量就得到微分方程组

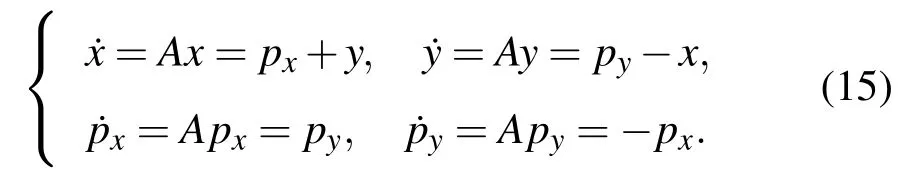
从初始状态量(x0,y0,px0,py0)出发经过时间t后获得该方程组的分析解为这意味着混合算子A是可积可解的.关于V的动量型算子B也是如此,但若非惯性系所施加的影响部分ypx-xpy与V结合便是不可积、不可解的.

当(14)式所给算子A代替(2)式中的算子A,我们容易证明(4)和(5)两式仍然成立,从而(6)式也仍然适用,即动量型算子

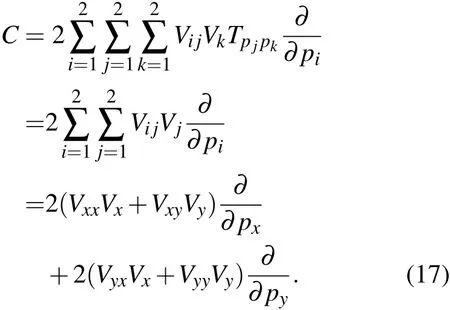
这表明算子C还是两主天体引力的梯度,并不是两主天体引力与旋转坐标系所附加非惯性力的合力之梯度.因此,旋转坐标系下的圆型限制性三体问题仍可如(1)式所示Hamilton系统那样用力梯度方法求解.为了更清楚地说明力梯度辛方法的具体实现过程,我们以算法S1为例列举其从l步到(l+1)步的差分格式

我们采用Jacobi常数CJ=3.12及大约相当于木星与太阳质量比参数µ=0.001和初值x=0.29,y=px=0,而初值py从能量积分(10)式或Jacobi积分(12)式确定并在开方运算中取正根.该积分轨道是图1(a)所示Poincare´截面y=0(y˙＞0)上的一个环,表明是拟周期有序轨道.让步长τ从0.01到0.1逐次变大,可得图1(b)所示的每个算法对每个给定步长积分100000步后的最大Jacobi常数误差.该图揭示了非力梯度Forest-Ruth辛方法S3的精度要显著劣于力梯度算法S1精度.还可以看出最优化力梯度算法S2是最好的.

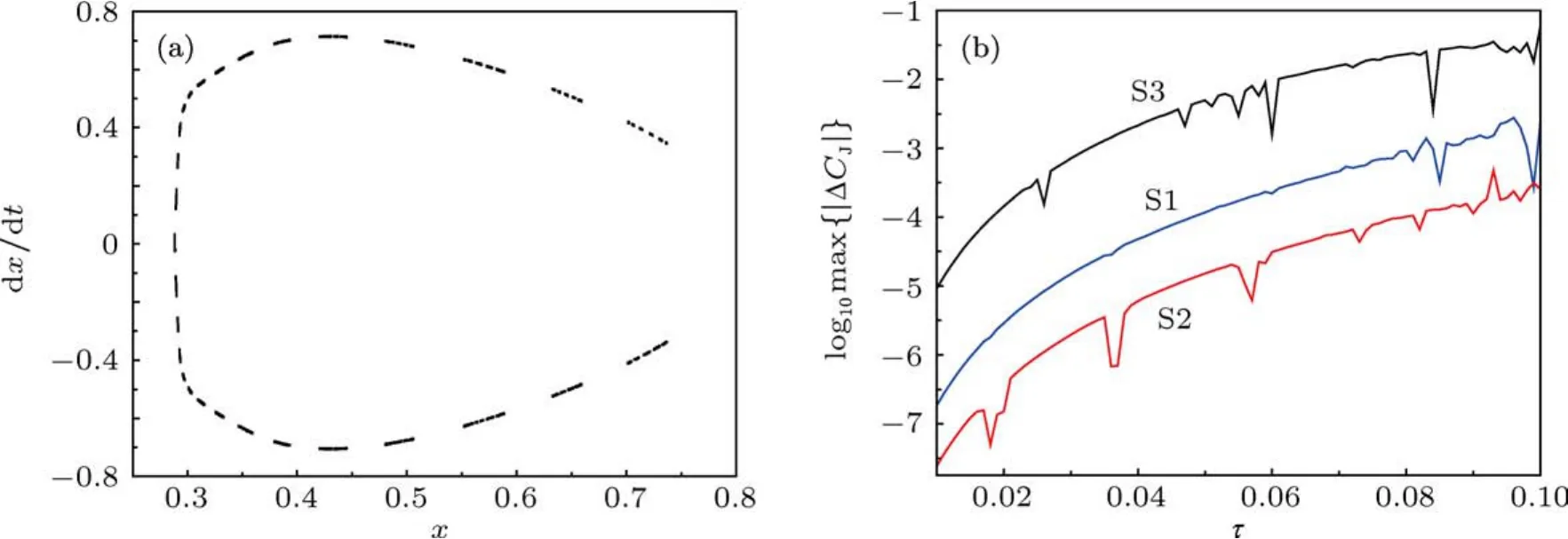
图1 (a)Jacobi常数C J=3.12的Poincar´e截面y=0上的拟周期有序轨道;(b)三个算法对每个给定步长积分100000步后的最大Jacobi常数误差

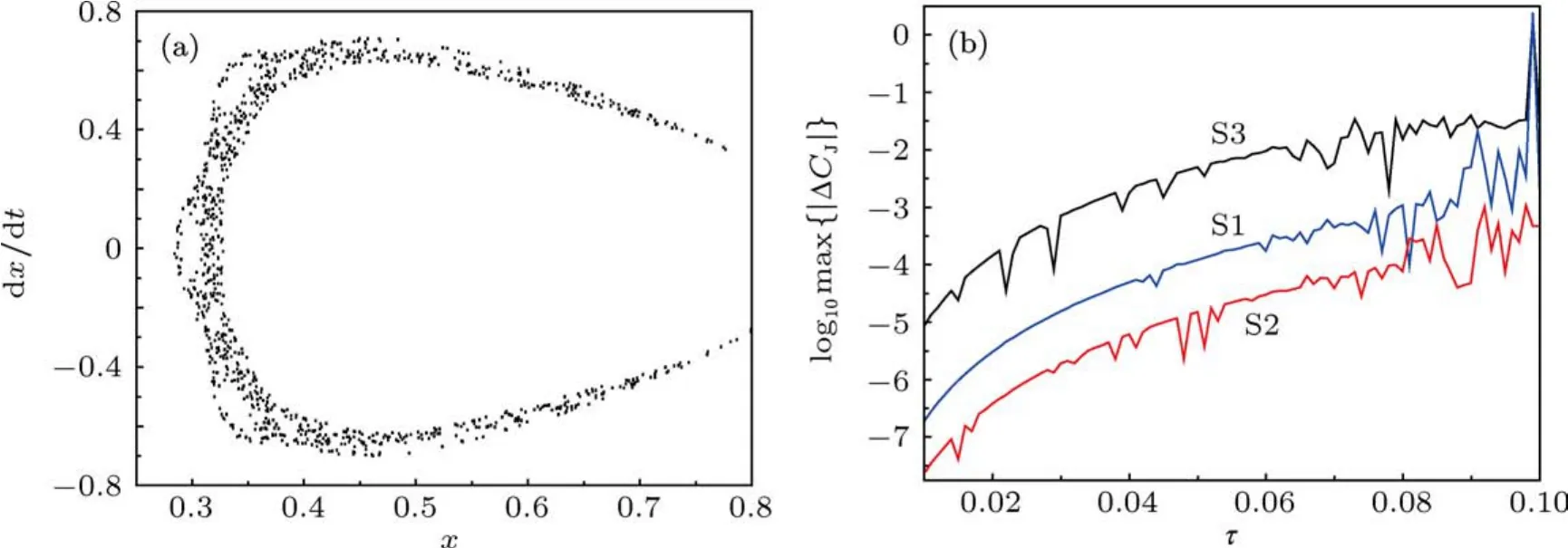
图2 (a)Jacobi常数C J=3.06的Poincar´e截面y=0上的混沌轨道;(b)三个算法对每个给定步长积分100000步后的最大Jacobi常数误差

当仅改变Jacobi常数CJ=3.06及相应初值py时,则得图2(a)所示Poincar´e截面上的一些随机分布的点,表明是混沌轨道.图2(b)的最大Jacobi常数误差再次证实三个算法的数值性能优劣关系与有序轨道的情形是完全一致的.就图1(b)和2(b)比较来看,当步长τ没有达到0.1前,对于有序和混沌轨道两情形每个算法精度基本上差不多;但当步长τ接近0.1时,针对混沌轨道情况,两算法S1和S3已失去数值稳定性,而算法S2仍几乎保持有序轨道的精度.

因此,无论是对有序轨道还是对混沌轨道进行数值模拟,我们总是发现力梯度类算法精度要大大优于非力梯度类的,而最优化型算法能够取得最好精度.这样,高精度辛方法的使用能确保所得动力学定性结果的可靠.下面我们考虑方法S2在混沌动力学方面的应用.

3.3 混沌指标

除Poincar´e截面方法外,Lyapunov指数和快速Lyapunov指标等都是区分系统有序与混沌的常用方法.这些方法克服了Poincare´截面限于相空间维数为3的应用局限,并且均以计算两邻近轨道的分离演化为基础来获得.

Lyapunov指数是衡量两邻近轨道平均指数分离比的指标.通常采用的是最大Lyapunov指数,定义为

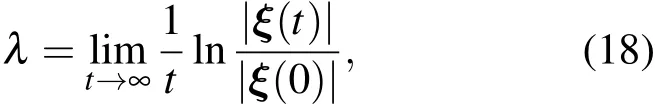
式中的ξ(t)和ξ(0)分别是t时刻与初始时刻的切向量,即变分方程之解.(18)式称为计算Lyapunov指数的变分法[33].当然,它的计算也可用两邻近轨道的差来代替变分方程之解,称为计算Lyapunov指数的两粒子法[33],定义如下：

d(t)和d(0)是两邻近轨道分别在t时刻与初始时刻的距离.应当注意初始距离必须适当选择,如果d(0)太大,那么两邻近轨道的差将与变分方程的解差别太大;但若d(0)太小,则舍入误差增大.也就是说,d(0)太大和太小都会导致不正确的Lyapunov指数.文献[36]认为就双精度而言初始距离的适当选择为d(0)=10-8,还指出应适当考虑重整化次数.对于有界轨道,若λ＞0,则系统混沌;当λ=0时,系统被认为是有序的.这是Lyapunov指数区分有序和混沌的准则.

注意(19)式代替(18)式计算Lyapunov指数的优点有二：对于复杂的动力系统,如相对论引力系统,可以避免推导复杂变分方程的麻烦;针对Hamilton系统来说,可以完全确保辛方法贯穿于Lyapunov指数计算的全过程,因为两粒子法就是用辛方法积分运动方程两次来计算Lyapunov指数.基于此因,我们采用两粒子法计算Lyapunov指数.选取步长τ=0.01,参数和参考轨道初始条件同上,而邻近轨道初始条件为x=0.29+10-8,其他初始条件与参考轨道的相同但初值py相应改变.每积分10步,实施一次重整化.于是,我们获得图3中的Lyapunov指数.图1轨道的Lyapunov指数λ趋于0故为有序的,而图2轨道的λ=0.023则表明其混沌性.

一个比Lyapunov指数区分有序与混沌更灵敏、更快的方法是快速Lyapunov指标,其定义如下[37]：

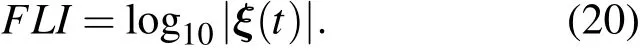
也可用两邻近轨道的差来代替变分方程之解来计算快速Lyapunov指标,称为两邻近轨道(或两粒子法)的快速Lyapunov指标[34],定义为

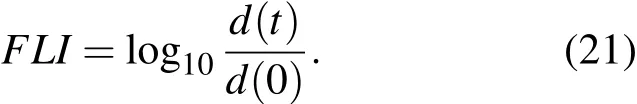
不同于(20)式,(21)式计算快速Lyapunov指标需要重整化,否则,混沌情形的两邻近轨道距离d(t)达到1后出现轨道饱和使其不再增长、计算无法继续.为避免这一问题,每当d(t)=1实施重整化,即不改变方向将邻近轨道拉回到与参考轨道相距d(0)处进行它的下次积分.假设重整化次数为k,那么,两粒子法的快速Lyapunov指标实际按下式计算

对于有序和混沌两种情况,切向量长度随时间演化的速度是完全不同的,即有序系统的切向量长度随时间代数式变大,而混沌系统的切向量长度随时间指数式增长.这一特性可以作为有序与混沌的区分标准.

由于两邻近轨道的快速Lyapunov指标具有两粒子法计算Lyapunov指数那样的优点,我们考虑它的应用.选择邻近轨道初始条件为x=0.29+10-9,其他初始条件和参考轨道的与上面相同但初值py相应改变.实际上,初始距离为d(0)≈10-9,可以比两粒子法的Lyapunov指数的初始距离要小些,而且重整化时间间隔要大很多.如图4所示,图1轨道的快速Lyapunov指标随时间增长缓慢,属于有序轨道类型;图2轨道的快速Lyapunov指标随时间增长迅速,应归之于混沌轨道一类.

对比图3和图4还可以看出利用Lyapunov指数区分有序与混沌需要积分的时间至少为t=10000,而根据快速Lyapunov指标只需积分到t=1000即可分辨两轨道类型.快速Lyapunov指标由于拥有识别混沌速度快的优点,因而常用来追踪小行星轨道稳定性和研究其他动力学问题[38-40].

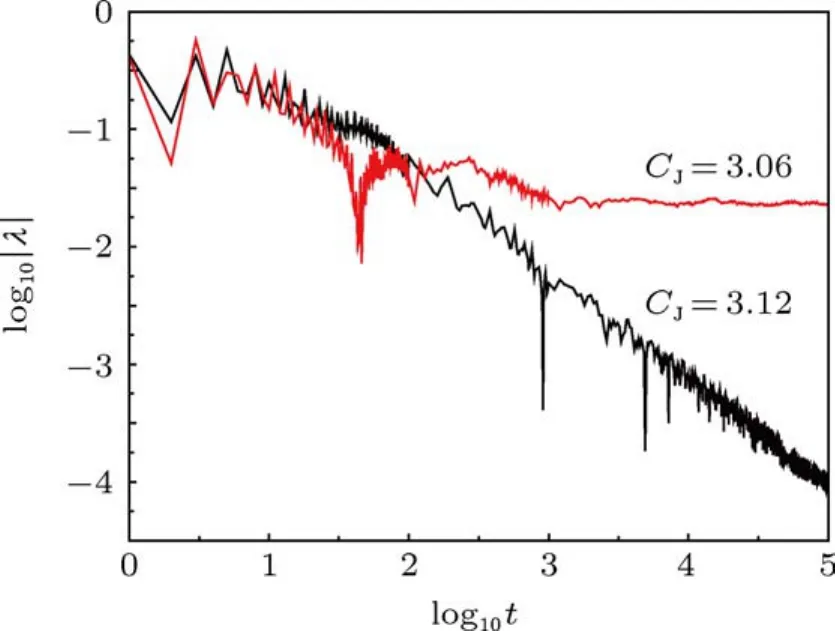
图3 两轨道的Lyapunov指数

图4 两轨道的快速Lyapunov指标

4 结论

旋转坐标系下的圆型限制性三体问题因含非惯性系所附加的影响部分使得动能不是动量的严格二次型,意味着力梯度辛积分算法的应用似乎遇到了理论方面的困难.本文从Lie算子运算出发严格推导了力梯度算子的物理意义仍然是两主天体对第三个小天体引力的梯度,并不是两主天体引力与旋转坐标系所附加非惯性力的合力之梯度.这样,解决了力梯度辛方法应用的理论问题.数值实验揭示力梯度类算法精度总要大大优于非力梯度类的,而最优化型算法能够取得最好精度.将最优化型算法计算两邻近轨道的Lyapunov指数和快速Lyapunov指标可以完全确保高精度辛方法能够贯穿于这些混沌指标计算的全过程,以便准确刻画动力学定性性质.

未来的工作希望借助这种最优化型辛积分算法和恰当的混沌指标探讨含辐射压的平面圆型限制性三体问题、平面椭圆型限制性三体问题、空间圆型限制性三体问题和空间椭圆型限制性三体问题等动力学性质.

[1]Feng K,Qin M Z 2009 Symplectic Geometric Algorithmsfor Hamiltonian Systems(Hangzhou：Zhejiang Scienceand Technology Publishing House)

[2]Zhong SY,Wu X 2010 Phys.Rev.D 81 104037

[3]Mei L J,Wu X,Liu FY 2012 Chin.Phys.Lett.29 050201

[4]Hairer E,Lubich C,Wanner G 1999 Geometric Numerical Integration.(Berlin：Springer)

[5]Chi Y H,Liu X S,Ding PZ 2006 Acta Phys.Sin.55 6320(in Chinese)[匙玉华,刘学深,丁培柱2006物理学报55 6320]

[6]Luo X Y,Liu X S,Ding PZ 2007 Acta Phys.Sin.56 604(in Chinese)[罗香怡,刘学深,丁培柱2007物理学报56 604]

[7]Liu X S,Wei JY,Ding PZ 2005 Chin.Phys.14 231

[8]Bian X B,Qiao H X,Shi T Y 2007 Chin.Phys.16 1822

[9]Cao Y,Yang K Q 2003 Acta Phys.Sin.52 1984(in Chinese)[曹禹,杨孔庆2003物理学报52 1984]

[10]Hu WP,Deng Z C 2008 Chin.Phys.B 17 3923

[11]Zhong SY,Wu X,Liu SQ,Deng X F 2010 Phys.Rev.D 82 124040

[12]Zhong SY,Wu X 2011 Acta Phys.Sin.60 090402(in Chinese)[钟双英,伍歆2011物理学报60 090402]

[13]Zhong SY,Liu S 2012 Acta Phys.Sin.61 120401(in Chinese)[钟双英,刘崧2012物理学报61 120401]

[14]Wu X,Zhong SY 2011 Gen.Relat.Gravit.43 2185

[15]Ruth RD 1983 IEEETran.Nucl.Sci.30 2669

[16]Preto M,Saha P 2009 Astrophy.J.703 1743

[17]Liao X H 1997 Celest.Mech.Dyn.Astron.66 243

[18]Lubich C,Walther B,Braugmann B 2010 Phys.Rev.D 81 104025

[19]Forest E,Ruth RD 1990 Physica D 43 105

[20]Yoshida H 1990 Phys.Lett.A 150 262

[21]Wisdom J,Holman M 1991 Astron.J.102 1528

[22]Preto M,Tremaine S 1999 Astron.J.118 2532

[23]Laskar J,Robutel P 2001 Celest.Mech.Dyn.Astron.80 39

[24]Wisdom J,Holman M,Touma J1996 Fields Inst.Commun.10 217

[25]Chin SA 1997 Phys.Lett.A 75 226

[26]Chin SA,Chen CR 2005 Celest.Mech.Dyn.Astron.91 301

[27]Chin SA 2007 Phys.Rev.E 75 036701

[28]Xu J,Wu X 2010 Res.Astron.Astrophys.10 173

[29]Sun W,Wu X,Huang G Q 2011 Res.Astron.Astrophys.11 353

[30]Li R,Wu X 2010 Science China：Physics,Mechanics&Astronomy 53 1600

[31]Omelyan IP,Mryglod IM,Folk R 2003 Comput.Phys.Commun.151 272

[32]Li R,Wu X 2010 Acta Phys.Sin.59 7135(in Chinese)[李荣,伍歆2010物理学报59 7135]

[33]Wu X,Huang T Y 2003 Phys.Lett.A 313 77

[34]Wu X,Huang T Y,Zhang H 2006 Phys.Rev.D 74 083001

[35]Murray C D,Dermott SF 1999 Solar System Dynamics(Cambridge,UK：Cambridge Univ.Press)

[36]Tancredi G,S´anchez A,Roig F 2001 Astron.J.121 1171

[37]Froeschl´e C,Lega E 2000 Celest.Mech.Dyn.Astron.78 167

[38]Wu X,Xie Y 2008 Phys.Rev.D 77 103012

[39]Wang Y,Wu X 2012 Chin.Phys.B 21 050504

[40]Wang Y Z,Wu X,Zhong S Y 2012 Acta Phys.Sin.61 160401(in Chinese)[王玉诏,伍歆,钟双英2012物理学报61 160401]