小通道氮气-水两相流三谱切片波动特性及其流型表征*

李洪伟 周云龙 王世勇 孙斌

1)(东北电力大学能源与动力工程学院,吉林 132012)

2)(抚顺矿业中机热电有限责任公司,抚顺 113001)

(2013年1月22日收到;2013年4月7日收到修改稿)

1 引言

小通道两相流广泛地存在于石油、化工和能源等现代工业领域.与常规通道相比,微尺度通道的尺寸减小2—3数量级,使其两相流动特性表现出与常规通道尺度下的流动特性有很大区别,这主要是因为在微小通道内两相间的表面张力和润湿性等处于主导地位.由于气液两相间内在的复杂性,有关微小通道内气液两相流动特性的研究仅仅处于初级阶段,但是因其在化学、化工和能源方面得到广泛的应用,所以一直以来都受到人们的广泛关注[1,2].

两相流是一个复杂的非线性动力学系统,自20世纪90年代以来,基于混沌、分形、复杂网络以及时频域分析等方法进行流型识别的研究日趋增多[3],文献[4—7]采用多个混沌参数指标、有限穿越可视图以及相空间多元图重心轨迹等方法分析了油水和气液两相流型电导信号的动力学特性,在揭示两相流型流动机理方面取得了一定进展.Sun等[8,9]应用自适应最优核时频分析方法对水平文丘里管内气液两相流型与流动特性进行了识别与分析.Du等[10]同样应用自适应最优核时频表征方法对气液两相流电导信号进行了分析,通过提取总能量和时频熵两个特征值准确区分出不同流型.Manfredo[11]基于气液两相流图像信号相密度时频分布特征对其流动特性进行了表征.Ommen等[12]对两相流时频域分析方法进行了综述,分析了在表征两相流流型动力学特性方面的各自优势与不足.

高阶谱估计技术是分析非高斯信号的有力工具,它从更高阶概率结构表征随机信号,可以弥补二阶统计量(功率谱)不包含相位信息的缺陷.高阶谱有很强的消噪能力,能够辨识非因果、非最小相位系统,检测和表征系统的非线性等[13].高阶谱中Welch,AR和EV功率谱近年来被广泛应用,但几种分析方法或多或少存在一些问题,最为普遍的缺点是抗噪能力不强且丧失了相位信息,这在非线性系统分析中是致命的弱点.而由文献[14]演化而来的三谱估计可以有效地规避上述问题,其1.5维切片对系统内在动力学特性揭示更加直观及具体.

目前流型研究大都集中在常规管道和微米级通道,而介于两种尺度之间的毫米级小通道(尤其是1.0—5.0 mm)的研究成果相对匮乏,相关文献报道很少.基于此,本文应用基于三谱切片的波动特性理论,针对内径2.0 mm×0.81 mm矩形垂直玻璃管道内的气液两相流流型动力学特性进行了研究.

2 理论基础

2.1 高阶谱

高阶谱分析是一种新的信号处理的有效技术,它可以定量描写信号间的非线性耦合,可以抑制噪声、保留信号的相位信息,是处理非线性、非高斯信号的有力工具[15,16].

设系统的传递函数为H(X),而a(t)为零均值的非高斯白噪声,由于采样信号常受到加性高斯噪声u(t)的干扰,用传统的时间序列建模无法排除加性的高斯噪声干扰.设y1(t)为y(t)中去掉确定性信号的零均值的有色随机信号,利用y1(t)的高阶累积量进行建模就可以抑制u(t)的干扰.对(2)式中的高阶累积量 cy,k(τ1,τ2,···,τk-1) 进行 k-1 维的离散Fourier变换,得到高阶谱的一般定义为

(1)式中,ω为频率,H(ω)为系统的传递函数,H∗(ω) 为 H(ω) 的共轭函数,Sy,k(ω1,ω2,···,ωk-1)为高阶谱,也被称为高阶累积量谱.当k=2,3,4时,它分别表示功率谱 P(ω)、双谱B(ω1,ω2)和三谱T(ω1,ω2,ω3).

2.2 自回归三谱

自回归(AR)模型,

式中,ai(i=1,2,···,p)为自回归系数,p为自回归模型的阶数.对于稳定的线性物理过程h(t),考虑到系统为最小相位系统,根据(1)式得到基于AR模型的双谱和三谱表达式分别为

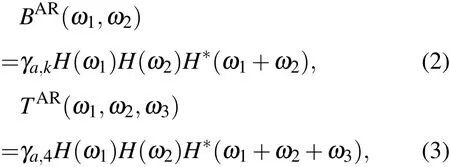
对y1(t)运用AR模型的参数法估计出模型系数a,结合(4)式将系数a代人(2)式和(3)式,得到AR双谱和三谱幅值为

2.3 切片谱

二次相位耦合是常见的一种现象.对于这种非线性耦合现象,仅用功率谱很难从根本上解决问题,而高阶谱就可以定量地描述二次相位耦合程度.当冻结三谱 TAR(ω1,ω2,ω3)中的一个频率 ω3,即当ω3=C(const)时,三谱切片就变成了双谱[17].定义三谱二维切片为

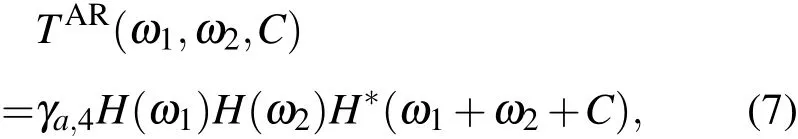
其规一化后的幅值为

用三谱切片谱函数计算二次相位耦合(信号两种主要振荡模式相互耦合),存在计算量大、三维图形不够直观等缺点.为了改善图形显示不够直观的缺点,采用二维的对角切片谱函数表征系统的1二次相位耦合程度.当ω1=ω2时,定义双谱的12维(对角)切片谱函数为

2.4 波动特征参数

概率密度分布为非正态分布的随机信号统称非高斯信号,在工程中通常用偏斜因子S,平坦因子K和波动强度σ/〈p〉三个参数来描述.本文将这三个参数应用到三谱切片的分析中,实现了三谱切片谱的定量分析.

式中x为离散时间序列,N为序列长度,E(·)为括号内均值.波动强度反映了序列幅值变化梯度的强烈程度,偏斜因子是衡量随机信号的分布偏离对称分布的歪斜程度,偏斜因子不等于零的信号必定服从非对称分布;而平坦因子表征统计频率曲线接近分布中心时的大致状态.这三个参数都从不同方面反映出了序列的复杂程度.

3 方法评价

为了评价本文提出的方法在时间序列的处理分析中的有效性,本文主要将抗噪性与复杂度表征性作为评价指标,从具有代表性的分形、周期、混沌时间序列着手考察该方法在处理不同类型时间序列所表现出的抗噪与表征能力.

3.1 分形时间序列

本文对Brown分形序列进行分析,考察三谱切片波动方法在处理分形序列时抗噪与辨识方面所表现出的能力.

分形Brown运动(fractional Brownian motion,fbm)是典型的随机性分形,其方程 f(x)是一个实值随机方程{：}

其中,x是E维欧空间RE中的一点;F(t)为随机变量t的分布函数,该随机变量服从标准正态分布 N(0,σ2);‖Δx‖ 为采样间隔;H 为 Hurst指数[6].本文采用Matlab中的wfbm函数生成长度分别为10000,5000,1000,500的分形Brown序列各5组,分别取Hurst指数H=0.1,H=0.3,H=0.5,H=0.7,H=0.9,结果示于图1.

本文对Brown分形序列的分析有两个目的：一是验证三谱切片的抗噪性能,二是讨论三谱切片计算过程中数据的长度与快速傅里叶变换(FFT)长度对辨识结果的影响.

图1 分形Brown运动时间序列

图2 是Brown序列三谱图,Brown分形序列虽然表面上看杂乱无章,但从图中还是可以看到Brown分形序列的内在规律性.二次耦合点主要集中在中心部位,接近于高斯分布.图3是分形Brown序列在不同噪声强度干扰下的三谱切片图.从图3中可以看出,五种强度噪声干扰下的功率谱线趋势基本相同,只存在微小的细节波动,再次验证了三谱切片良好的抗噪性能.

在计算同一种时间序列的三谱切片及波动特征值过程中,我们发现有两个参数对计算结果的影响比较大,一个是所取的序列长度N,另外一个是在进行FFT变换过程中所选择的长度nFFT.本文对分形Brown运动时间序列在取不同H值情况下进行了N与nFFT的正交计算,观察每相邻两组H值的三个波动特征参数类间距值,长度为10000时的具体数据如表1所示.

图2 分形Brown序列三谱图(H=0.1,N=10000)

图3 Brown序列不同加噪下三谱图(H=0.1,N=10000)

从表1中可以很清楚地看到,在没有噪声干扰下的分形Brown序列随着nFFT的减小三个波动特征参数间的差值逐渐减小,当nFFT为64时,每相邻两组序列的间距值只有一组不为0,且这一组中也只有波动强度值不为0,平坦因子和偏斜因子也为0.这表明在同一长度N下nFFT值越大,波动特征参数间的差值越大,辨识度越高.对于不同长度的分形Brown序列又有什么规律,在加入噪声干扰情况下规律是否发生变化,图4给出了详细的说明.从图4中可以看出,在没有噪声干扰的情况下不同长度序列在取得最大类间距时的nFFT长度都固定为1024,是一条平行于x轴的直线,而在有噪声干扰的情况下,呈现出近似反比关系,当N越大nFFT取值越小.

表1 分形Brown序列不同n FFT时三个参数间距值

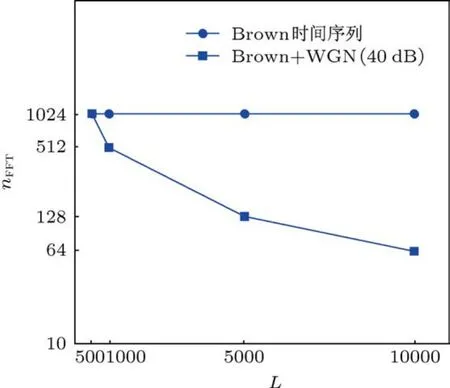
图4 Brown序列取得最大类间距值下的N与n FFT曲线

表明在时间序列严格符合高斯正态分布的情况下,N与nFFT两者越大辨识效果越好,在有不规则噪声干扰从而破坏正态分布结构的情况下,N与nFFT成反比关系.这也为后面流型差压序列分析时的参数选择提供了理论依据.

3.2 周期、混沌时间序列

本文为了考察三谱切片及其波动理论适用的广泛性,对正弦、正弦+噪声混合、Lorenz以及Lorenz+噪声混合四种典型信号进行分析计算.几种时间序列的产生条件如下：

1)正弦信号,y1=sin(x),采样间隔为π/50;

2)正弦+噪声,y=y1+p×y2,其中y1为正弦序列,y2为白噪声序列,p为随机成分的比例,这里取p=0.2;

3)Lorenz混沌信号,由Lorenz方程

初始条件x=2,y=2,z=20,采用四阶龙格-库塔方法迭代,取变量x为仿真序列[18];

4)Lorenz+噪声,3)中所得变量x+40 dB噪声.

图5 Lorenz与sin信号的加噪前后三谱切片图

图5 为抗噪性能检测,从图中很容易看出,三谱切片在处理混沌序列时抗噪效果非常好,加噪后与加噪前波动趋势几乎如出一辙,而在处理周期序列时受噪声扰动影响十分明显,抗噪性能相对较差.而图6则为四种信号三谱切片的波动特征值,从图中可以看出,每种信号的三个波动参数值排序为：

Lorenz+噪声＞Lorenz＞sin+噪声＞sin,这也正表征出四种信号的内在复杂程度.

图6 Lorenz与sin信号的加噪前后波动特征值分布

通过对分形序列、周期序列和混沌序列的应用分析,得出结论：三谱切片结合波动特性理论在处理分形和混沌序列时具有较好的抗噪能力,处理周期信号时抗噪能力相对较差.在复杂程度表征方面,无论应用在哪种类型的序列中都具有很好的效果.此外,在计算三谱切片过程中,序列长度N与nFFT的选择应遵循如下原则：在时间序列严格符合高斯正态分布的情况下,N与nFFT两者越大辨识效果越好,在有不规则噪声干扰从而破坏正态分布结构的情况下,N与nFFT近似成反比关系.

4 流型辨识及其动力学机理分析

实验系统如图7所示.该实验系统主要包括两部分,即气液两相流动与控制系统、数据采集系统.实验段采用透光性较好的有机玻璃制成.在通道相距200 mm处取两个直径为0.5 mm的取压小孔,上游小孔距通道入口100 mm,下游小孔距通道出口80 mm,矩形通道截面宽为2.00 mm,缝隙为0.81 mm.

实验中数据的采集主要有压差信号、单相气相流量和单相液相流量.其中：压差信号采用罗斯蒙特3051C差压变送器进行测量,测量精度为±0.075%,更新响应时间为100 ms/次,差压校验量程为0.5inH2O-2000psi,实验中采集压差信号的采样频率为256 Hz;液体流量测量采用HW5智能金属管浮子流量计,此流量计以MCU微处理器为核心,瞬时值和累计值的精度为±0.5%;气体流量测量采用型号为D-600MD数字式气体流量计,该流量计的量程范围为0—5 SLM,精度等级为±1%.实验中实验环境压力为0.1 MPa±0.0005 MPa,实验环境温度为25°C±0.5°C,表观气速为0.1—30 m/s,表观液速为0.01—5 m/s.

在图7中实验段上采集到四种典型流型的差压信号,并进行了三谱切片计算,结果如图8所示.

图7 氮气-水两相流实验系统

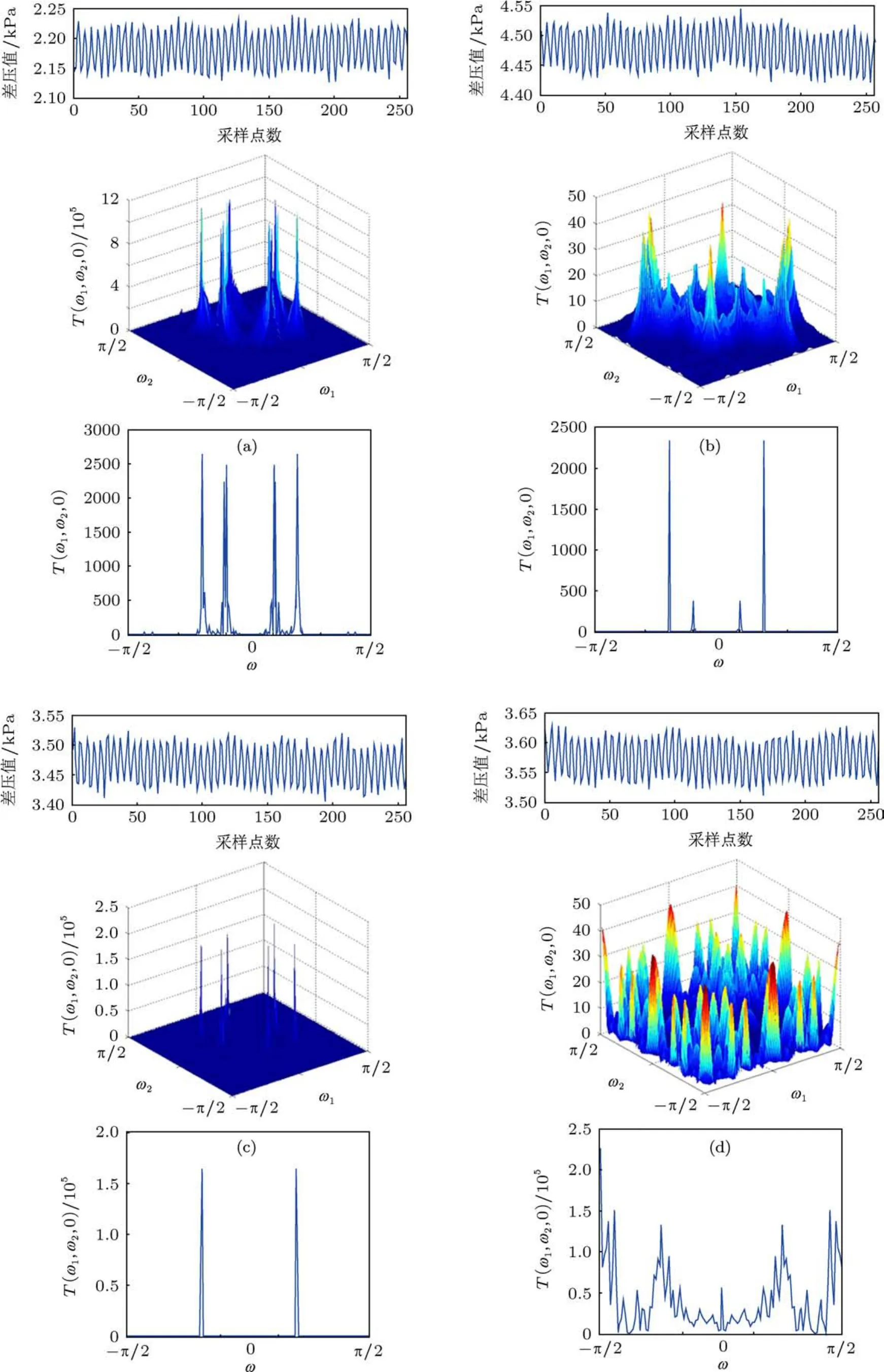
图8 氮气-水两相流典型流型差压信号、三谱图、切片图 (a)毛细泡状流;(b)分散泡状流;(c)段塞流;(d)环状流

从图8中可以看出,不同流型的三谱图表现差异较为明显,这是由于不同流型气液两相界面分布不同引起压降变化不同的结果.相较于三谱3D立体图的复杂等频对角切片更加直观,更能体现不同流型的相分布特点.主要通过对二次耦合谱线的判断挖掘气相与液相两种振荡频率与相位的耦合特性.小通道内氮气-水分布情况最为复杂的是环状流,其对角切片呈现出频率峰值分布混乱的特点,主要频率峰值出现在-π/2,-7π/16,-π/4,π/4以及π/16处,其他很多处也存在微小的耦合现象,说明气液两相振荡并无明显耦合处,对压降分布的影响也比较随机,主要是由于环状流是由段塞流演变而来,在段塞流中气流量继续增加使得气塞被击碎,形成不规则振荡式运动模式,附在小通道表面的液膜在气相推动下呈现出混沌、分形特征的抖动,而这种抖动的不规则性类似于信号当中加入了白噪声,其二次相位耦合也相对最为复杂.虽然耦合峰值不稳定,但从图8(d)可以看到环状流在不规则的切片谱上还是存在几处相对较为明显的峰值.这种不稳定峰值形成的原因有两种：一方面是实验系统中氮气瓶输出气体时的波动以及气体流经三通时分配不均匀形成的波动.而这种波动反映到实验段中存在一定的延迟,使得实验段中环状流的液膜被气相冲击产生振荡存在一定的间歇性,这样就形成了切片谱中的耦合双峰值;另一方面是环状流的波动近似混沌、分形并掺有白噪声,这种不规则振荡信号本身存在一定的相位周期性,这种周期性使得环状流切片谱中出现类似图3和图5的几处峰值.

从图8(a)和图8(b)中可以看到毛细泡状流在-π/4到π/4之间存在四处明显峰值,而分散泡状流外侧两个峰值与毛细泡状流较相近,中间两个峰值相对较小,这与两种不同类型的泡状流气泡尺寸大小与间隔频率不同有关,毛细泡状流中气泡尺寸分布均匀,间隔频率具有很好的规律性,所以其两相振荡频率耦合谱线明显,而分散泡状流气泡尺寸分布不如毛细泡状流均匀.同时两种泡状流的运动特征存在明显的差异.气液两相流体以毛细泡状流型流动时,生成的均匀气泡与矩形管道的两壁相贴,气泡的截面积和小通道的横截面积近似等同,液相不再连续.随着气流量的波动,所生成的气泡时间间隔大概在平均值的上下波动,这样气泡与液塞以几种周期间歇性运动.由于三谱切片主要考察的是信号本身两种主要振荡模式的耦合现象,将高于平均值的时间间隔定位一种周期,那么平均值以下的是另外一种周期,所以从切片图中可以看到明显四峰值(两种周期).而分散泡状流由于不同尺寸的气泡均单独且分散地存在于连续液相之中,不具备毛细泡状流那样良好的周期间歇性,但由于气体流量的波动性,使得微小气泡在随着液相的运动过程所出现的量不完全一致,时多时少,正是这种原因使得分散泡状流的差压波动信号主振荡模式被气泡数量大和小的两种群体的间歇性出现所主宰,所以其切片谱中的双峰值现象明显,由于周期时间较长,所以峰值出现在外侧.而靠内侧的两个小的峰值是散落在液相当中小气泡连续不间断出现使得差压信号所产生的微小波动所致,由于周期性不明显,所以峰值不够突出.而段塞流由于其特殊的流动结构决定了它的气液两相振荡模式耦合特别明显(如图8(c)所示),而且由此可以给出段塞流动的频率,在π/3左右(一种周期).

图9给出了四种典型流型差压信号的三谱切片波动特征值分布情况,通过特征值的分布可以实现对流型的辨识.通过图9(d)可以发现S与K相结合对段塞流的分类效果要明显好于其他两组组合,说明针对周期性较强的时间序列,由于其与高斯序列差距明显,应用S与K处理分析时会与其他接近分形、混沌的时间序列有较明显的差距,而在毛细泡状流、分散泡状流与环状流的识别上效果不是很理想,主要原因是由于这三种流型差压信号波动周期性不强,具有分形与混沌特征,在这种情况下,σ/〈p〉就显示出了它在处理接近高斯分布序列的优势,从图9(b),(c)可以看到,环状流的分类效果相对还是比较理想,但这三个波动特征参数任意两两组合的效果都不是十分完美,始终在毛细泡状流与分散泡状流的分类上存在一些瑕疵,总有部分流型样本混杂在一起,难以准确识别.而将三者结合到一起得到了对四种流型的满意识别结果(图9(a)).

5 结论

本文提出了一种基于三谱切片的波动特征分析理论,为了验证该方法的适用性,将其应用到分形、周期以及混沌时间序列,主要验证了该方法的抗噪能力与对复杂度表征能力.结果表明该方法在处理分形与混沌时间序列时抗噪能力比较突出,而对于周期序列相对较差,基于三谱切片的波动特征值 (σ/〈p〉,S,K)能够很好地表征出系统的复杂程度.同时发现在时间序列严格符合高斯正态分布的情况下,N与nFFT两者越大辨识效果越好,而在有不规则噪声干扰从而破坏正态分布结构的情况下,N与nFFT近似成反比关系.

通过将该方法应用到小通道氮气-水两相流差压信号中,发现四种典型流型三谱切片差异明显,主要振荡模式的耦合现象可以揭示出不同流型的内在流动机理,环状流较泡状流与段塞流更为复杂,其气相与液膜相互作用显示出强烈混沌特征,段塞流由于明显的周期性使得对角切片分布最为简单明了.

流型差压信号的三谱切片结合三个波动特征值实现了对四种典型流型的准确识别.其中S,K对非高斯信号识别效果比较突出,而σ/〈p〉对高斯信号的辨识度更高,将三者结合到一起可以使各自优势互补,实现小通道内氮气-水两相流型的准确识别.如将其应用于其他多相流流型识别领域,以及在其他模式识别领域进行拓展,也将是有益的探索与补充.

[1]Ding GL,Huang D P,Zhang CL 2002 Journal of Refrigeration 2 7(in Chinese)[丁国良,黄东平,张春路2002制冷学报2 7]

[2]Li H W,Zhou Y L,Liu X,Sun B 2012 Acta Phys.Sin.61 030508(in Chinese)[李洪伟,周云龙,刘旭,孙斌2012物理学报61 030508]

[3]Gao Z K,Jin N D 2008 Acta Phys.Sin.57 6909(in Chinese)[高忠科,金宁德2008物理学报57 6909]

[4]Zong Y B,Jin N D,Wang Z Y 2009 Acta Phys.Sin..57 7544(in Chinese)[宗艳波,金宁德,王振亚2009物理学报57 7544]

[5]Dong F,Jin ND,Zong Y B 2008 Acta Phys.Sin.57 6145(in Chinese)[董芳,金宁德,宗艳波2008物理学报57 6145]

[6]Zhou T T,Jin N D,Gao Z K 2012 Acta Phys.Sin.61 030506(in Chinese)[周婷婷,金宁德,高忠科2012物理学报61 030506]

[7]Zhao JY,Jin N D 2012 Acta Phys.Sin.61 094701(in Chinese)[赵俊英,金宁德2012物理学报61 094701]

[8]Sun B,Wang EP,Ding Y 2011 Chinese Journal of Chemical Engineering 19 243

[9]Sun B,Wang E P,Zheng Y J 2011 Acta Phys.Sin.60 014701(in Chinese)[孙斌,王二朋,郑永军2011物理学报60 014701]

[10]Du M,Jin N D,Gao Z K 2012 Chem.Engin.Sci.82 144

[11]Manfredo G 2013 Int.J.Multiphase Flow 51 1

[12]van Ommen JR,Sasic S,van der Schaaf J,Gheorghiu S,Johnsson F,Coppens M 2011 Int.J.Multiphase Flow 37 403

[13]Barker RW,Klutke G,Hinich M J1993 ASMETrans.115 23

[14]Zhang Y,Wang S X,Li S H 1996 Acta Electron.Sin.24 109(in Chinese)[张严,王树勋,李生红1996电子学报24 109]

[15]Lutes L D,Chen D CK 1991 Int.J.Non-Linear Mech.6 893

[16]Hinich M J1994 Circuits Sys.Signal Proc.13 391

[17]Zhang W J,Huang Y J 2009 Machine Tool and Hydraulics 37 52(in Chinese)[张文俊,黄宜坚2009机床与液压37 52]

[18]Zheng GB,Jin N D 2009 Acta Phys.Sin.58 4485(in Chinese)[郑桂波,金宁德2009物理学报58 4485]