各地区高等院校科研状况的综合评价分析①

潘玉荣， 贾朝勇

(蚌埠学院数理系，安徽 蚌埠 233000)

0 引言

我国普通高等院校肩负着人才培养、科学研究、社会服务三大任务，科学研究常常围绕人才培养、教学的相关问题展开，可以促进教学的深入和提高，教学又为高校的教师和学生参与科学研究活动提供了可能，而搞好科学研究可以使高校更好的为社会服务.科学研究成果是衡量高校总体实力的一个重要指标，科研的状况也直接影响高校的排名，因此，找出影响高等院校的科研状况的关键因素，正确合理评价各地区高等院校的科学研究的整体状况是很必要的.描述科研状况变量很多，比如投入科研活动的人年数、投入高级职称人年数、投入科研事业费、课题总数、专著数、论文数、获奖数等，但并非收集的变量越多对问题分析越有利，因变量间信息的高度重叠和高度相关反而会给统计方法的应用带来许多障碍，甚至使分析结果不准确.针对此问题，选用1999年我国31个省市自治区部分高校有关人文社会科研究方面的数据为样本资料，借助SPSS软件，运用多元分析方法中的因子分析方法[1～2]，从众多变量中提取影响高校科研状况的主要因子，并借鉴国内一些学者的研究成果[3～6]，对各地区高校科研状况进行科学合理地评价.最后通过因子变量的聚类分析对评价结果进行验证.

1 因子分析方法简介

因子分析主要利用数学上的变量降维思想，将实际问题中的多个指标设法重新组合成一组新的少数几个综合指标来代替原来指标的一种多元统计方法.通常把转化生成的综合指标称为因子，其中每个因子都是原始变量的线性组合，且各个因子之间互不相关，还要尽可能多的反映原来指标的信息.因子分析的基本步骤为:(1)因子分析前提条件的验证，因子分析前提条件要求原始变量之间应存在较强的相关关系，这样才能进行因子的提取;(2)因子的提取，因子提取个数确定是很重要，因子要反应原有变量的绝大部分信息;(3)使因子具有命名可解释性，提取的因子被确定后，还需根据因子的旋转获得命名可解释性;(4)计算各样本的因子得分，根据因子得分系数矩阵计算样本数据的因子得分，从而获得因子变量.其中，因子的提取是很关键的步骤，常用的提取方法是主成分分析法.

2 各地区高等院校科研状况的因子分析

2.1 数据的来源和指标选取

本文选用的数据是1999年我国31个省市自治区部分高校有关社科研究方面的数据，数据主要来源于薛薇《SPSS统计分析方法及应用》，数据中7个指标变量是对高校科研状况较全面的描述，其中X1—省市名称，X2—投入人年数，X3—投入高级职称人年数，X4—投入科研事业费(百元)，X5—课题总数，X6—专著数，X7—论文数，X8—获奖数.

根据SPSS软件对上述的7个指标变量的相关性进行分析，从变量的相关系数矩阵(见表1)发现相关系数大部分多大于0.6，说明各变量呈较强的线性关系，能够从中提取公共因子.另外从表2中，发现KMO统计量值是0.846，也说明这些变量相关性很强，适合作因子分析，Bartlett＇s球度检验的实测概率为0小于显著水平0.05，应拒绝原假设，进一步说明这7个指标变量相关性强，适合作因子分析.

表1 变量的相关系数矩阵表

表2 Bartlett＇s球度检验和KMO检验

2.2 因子提取和因子命名

由于描述各地区高等院校社会科研状况的7个指标变量相关性较强，适合作因子分析，现应用主成分分析法来进行因子的提取和因子个数的确定，从表3的因子方差累计贡献率发现第一个因子的特征根为5.994，解释原有7个变量总方差的85.631%，而当提取两个因子时，对原变量的方差解释能力达到94.889%，远远大于85%的要求，故取前面两个因子基本包含了全部测评指标所具有绝大部分的信息，因子分析效果较理想.

表3 因子解释原有变量总方差的情况

表4 旋转后的因子载荷矩阵

投入人年数 0.840 0.512课题总数 0.826 0.490论文数 0.743 0.616获奖数0.258 0.949

为了给这两个因子命名，这里采用方差最大法对因子载荷矩阵实施正交旋转以使因子具有命名解释性.现指定按第一因子载荷降序的顺序输出旋转后的因子载荷以及旋转后的因子载荷图即表4，从表中可以得知科研人力投入(投入科研事业费)、经费投入(投入高级职称的人年数、投入人年数)等变量在第一个因子上有较高的载荷，说明第一个因子主要解释这几个变量，可解释为科研投入因子;而发表论文数、获奖数等变量在第二个因子有较高的载荷，说明第二个因子主要解释这几个变量，可解释为科研产出因子，即原有7个相关变量综合成科研投入、科研产出两个因子.

2.3 因子得分和因子变量

这里采用回归法估计因子得分系数，并输出因子得分系数矩阵见表5.

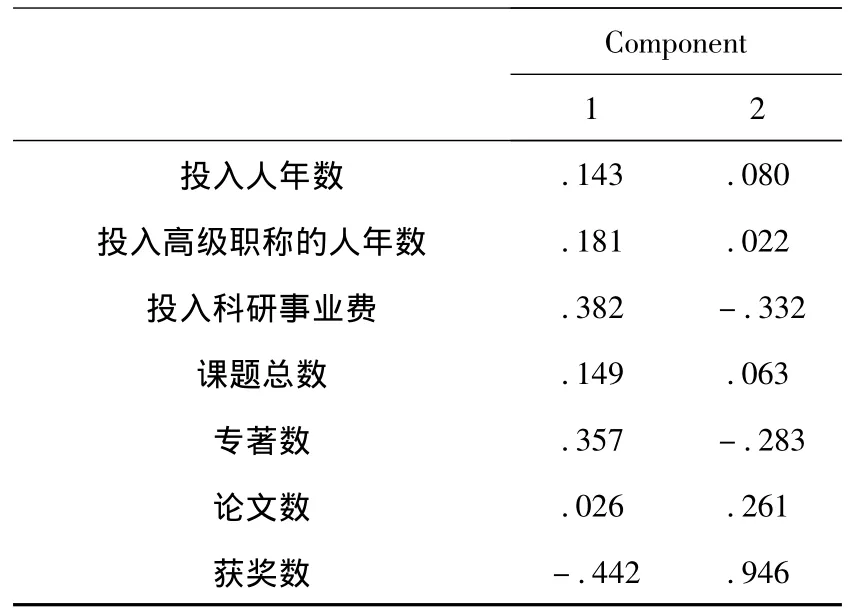
表5 因子得分系数矩阵

根据表5可写出以下因子得分函数:

F1=0.143投入人年数 +0.18投入高级职称的人年数+0.382投入科研事业费 +0.149课题总数+0.357专著数 +0.026论文数 －0.442获奖数(1)F2=0.08投入人年数 +0.022投入高级职称的人年数－0.332投入科研事业费 +0.063课题总数－0.283专著数 +0.261论文数 +0.946获奖数(2)

通过上述公式(1)和公式(2)可以得到每个地区的因子得分，从而获得两个因子变量，由于这两个因子变量是线性无关，因此，可以利用它们对各地区的高等院校的科研状况作统计分析.

3 各地区高等院校科研状况的综合评价分析

下面利用两个因子变量对各地区1999年高等院校科研状况进行多元统计分析，并对各地区高等院校科研状况进行评价.

首先，画出两因子变量的散点图对各地区高等院校科研状况进行对比分析.以第一因子变量科研投入因子为横坐标，以第二因子变量科研产出因子为纵坐标作出散点图如图1.观察图1可看到北京的第一因子很高，表明科研投入很大，远远高于其他地区.广东、湖北两个因子都高于其它地区，说明这两个地区的高校科研投入和产出都较高.江苏、山东、湖南、浙江和辽宁的第一因子与其他地区相差不大，但第二因子却较大，说明这些地区的高校科研产出较高.其他地区的科研投入和科研产出都相差不大.

图1 各地区两因子得分变量的散点图

其次，对各地区的1999年高等院校科研状况进行综合评价.这里采用加权总分的方法，其中权重就取两个因子的方差贡献率为权数，计算公式为F=0.856F1+0.9258F2，综合得分较高的省市有北京、江苏、山东、湖北、广东、湖南、上海、辽宁、浙江等，这些地区大多是我国的中东地区，高校相对较聚集.而综合得分较低为西藏、青海、宁夏、贵州等，多为西南部边远地区，这些地方的高校数量较少.这个结果与散点图分析的情况有很相似的地方.

最后，利用中心聚类对各地区的高等院校科研状况进行聚类分析，即利用两因子变量对31地区进行快速聚类，分成3类的结果如表6所示.北京独自成一类，辽宁、江苏、浙江、山东和湖南成一类，余下的地区成一类，这个结果与散点图分析、综合评价分析的情况基本类似.

表6 聚类结果

综上，从上述评价分析发现，各地区高校的科研状况总的来说具有不均衡性，究其原因相当复杂，中东地区因为地理位置和经济原因高校数量较多，投入科研的人力、物力、财力较多、以至科研投入和科研产出的总量相对高些，而西南部地区相对低些.

4 结束语

本文针对资料数据对各地区高校社科研状况进行综合评价分析.此分析思路即当要研究的问题涉及得变量很多，而且变量间的相关性较强时，可以采用因子分析法进行因子提取，利用因子变量进行事物的评价分析，有利于得到预期的分析效果.另外，就本案例而言，通过研究发现，因地理位置、经济状况等原因，我国各地区高等院校社科研状况总体而言具有不均衡性，所以要改善这种状况，建议国家增加对西南部边远地区教育及科研的人力、财力投入.

[1]薛薇.SPSS统计分析方法及应用[M].第二版.北京:电子工业出版社，2006:303 －349.

[2]张文彤.SPSS11统计分析教程—高级篇[M].北京:北京希望电子出版社，2002:166－210.

[3]阎慈琳.关于主成分分析做综合评价的若干问题[J].数理统计与管理，1998(2):22－24.

[4]宋之杰，高晓红.一种多指标综合评价中确定指标权重的方法[J].燕山大学学报，2002，1(26):20 －22.

[5]齐维毅，黄凤娟.因子分析在对学生考试成绩进行综合评价中的应用[J].沈阳体育学院学报.2000，1:55 －59.

[6]胡振华，袁静.因子分析在企业综合经济效益评价中的应用[J].中南工业大学学报，2001，37:214 －217.