基于快速DCT对插值数据的压缩储存①

陈秀荣， 周仲礼， 马 腾

(成都理工大学数学地质重点实验室，四川 成都 610059)

0 引言

伴随计算机图形技术的发展，三维地质模型已经被广泛应用在城市环境地质评价中.本文在三维地质建模中，以面模型为基础，对每一层钻井采样数据进行网格化，以高程值作为属性值，再经过克里格插值算法[1]进行属性插值计算获得足够的三维地质建模数据，从而实现对城市环境地质的地形模拟.

然而，往往实际的钻井采样数据总量非常大，经由这些数据进行网格化插值得到的数据量将更加庞大，如何将这些数据完好长久地储存就成为了一个问题.

采用基于二维DCT的JPEG静态图像压缩方法将很好的解决这一问题.其中的DCT变换虽然未能带来数据量的直接降低，但是它却能将被处理矩阵的能量集中在少数数据，从而很大程度上消除了数据间的相关性和冗余性.然而进行二维DCT变换需要的计算量很大，所以本文采用二维DCT的快速算法来进行数据压缩，从而取得即高效又实用的效果.

1 简介二维DCT变换[2－3]

由克里格算法进行属性插值得到了更多的高程值，将这些高程值组成的矩阵可视为静态图像像素点构成的矩阵，从而进行JPEG静态图像压缩的第一步映射变换，本文采用DCT变换.

二维DCT变换公式如下:

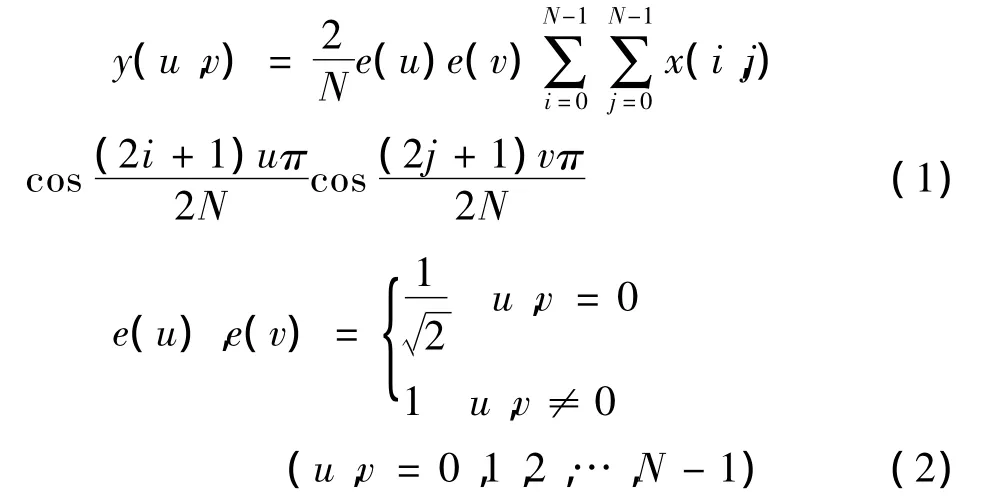
相较于傅里叶变换，DCT避免了复数运算，提高了运算效率.由于DCT为正交变换所以其反变换一定存在，则由反变换进行的数据重构可以实现，则DCT变换也就具有了实际意义.然而二维DCT变换涉及的运算往往需要大量的加法及乘法严重影响了变换速度，从实现角度考虑，需要引进二维DCT的快速算法.

2 简介快速 DCT算法[4－6]

在静态图像压缩处理中，往往将像素点构成矩阵分成若干子块分别进行处理.本文将待处理的原始数据矩阵分成8×8的子块，然后分别进行DCT变换.则对于每一个子块中进行一次列向量变换要进行56次加法和64次乘法.运算量显然过于庞大.然而采用DCT的快速算法则情况明显改善.

对于将子块矩阵的每一个列向量进行DCT变换，其实就是进行一维DCT变换，其公式可表示如下:

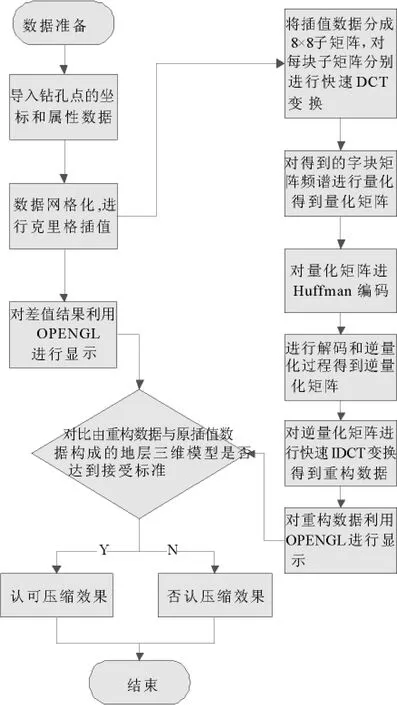
图1 数据压缩步骤流图

以离散傅里叶的快速算法FFT为依据，计算一个N点DCT可相当于进行2N点FFT，具体实现步骤如下:

1.把 x(n)补 N个0，从而形成2N点序列x2N(n);

2.通过FFT求x2N(n)的DFT，得到x2N(k);

3.将 x2N(k)与 e－jkπ/2N相乘，然后取其实部得到新的x2N(k);

4.令

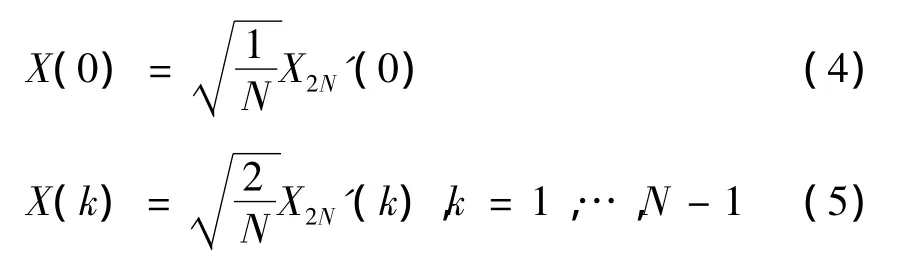
即完成整个N点DCT运算.

经过快速DCT运算，进行一次列向量变换实际相当于只进行了16次加法和16次乘法运算，显然需要的运算量大大减少.从而使DCT算法更加便于应用.

3 数据压缩分步流程图

本文对原始数据进行插值，继而进行数据压缩，最后进行数据重构的基本步骤流程如图1所示.

4 实例应用

本文利用VC开发平台结合OPENGL完成三维模型的建立.选择长沙作为城市地质调查试点.为了能够查明试点城市地质、资源及环境状况，对钻孔采样数据进行网格化插值处理继而进行三维地层模拟.

插值算法即选用克里格法，为方便展示，选用其中部分插值结果，利用VC及OPENGL结合开发进行分层显示如下图:

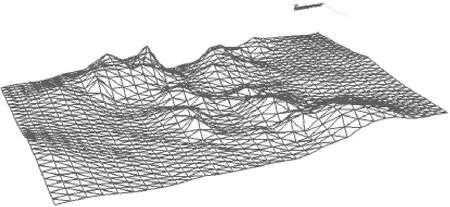
图2 克里格插值数据地层三维模拟

然后将克里格插值的数据进行压缩处理，数据压缩分为:映射变换、量化和编码三步[7－8].其中映射变换即为快速二维DCT变换，量化则使用JPEG经过大量测试推荐的8×8矩阵W，编码则对量化后矩阵进行Huffman编码.虽然经过压缩处理的数据所占磁盘空间大大减少，但是，这并不能表示数据压缩的效果达到要求.只有当压缩数据重构之后的结果没有明显失真时，才能确定压缩效果达到要求.所以，在压缩数据之后进行数据重构是必须的.具体的数据压缩及压缩数据重构过程如下:

1.将待压缩数据矩阵分成8×8的子块，选取子块矩阵中的一个矩阵记为S如下:

S=

2.将矩阵S进行二维快速DCT变换得到矩阵C:

3.选取JEPG推荐的默认8×8量化矩阵W[9]为:

3.对矩阵C经矩阵W进行量化得到矩阵C1，具体量化过程是C中的元素和W的元素对应相除后再取整.

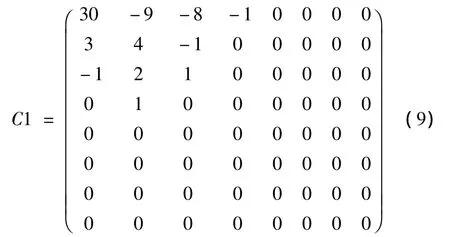
显然可以得到压缩比为4.

5.然后对矩阵 C 1 进行 Huffman 编码[10]，接着进行数据解码，由于Huffman编码可保证失真率为0，则经过解码，依然可以的得到矩阵C 1.

6.对矩阵C1通过矩阵W进行逆量化，得到矩阵C12:

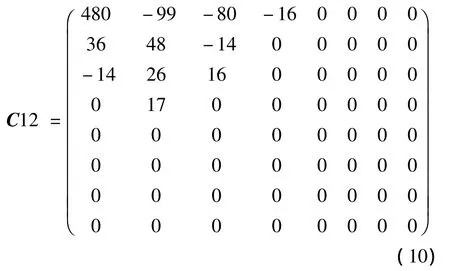
3.对矩阵C 12进行二维快速IDCT变换得到矩阵S1:

最后得到了经由压缩数据进行重构得来的数据，为了检验数据压缩的效果，依然利用VC结合OPENGL对重构数据进行分层显示如下图:

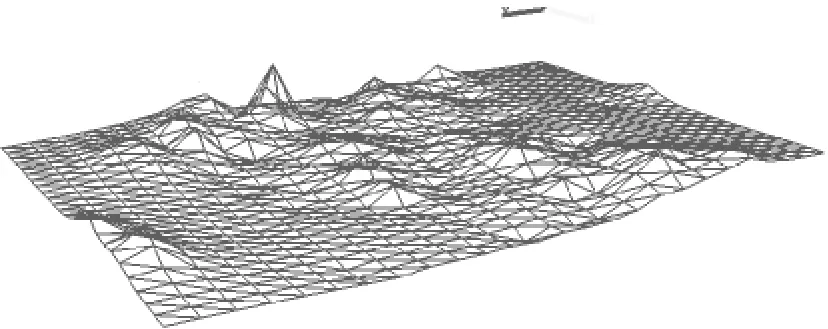
图3 经压缩的重构数据地层三维模拟

由上图与图2比较来看，绘制地层的基本走势未发生明显变化，那么显然压缩数据并未明显失真，所以作为有损压缩来说，压缩效果可以被认可.其中图3相较图2来看，显然在细节处图3不如图2走势平滑，且图2中局部的一些细微起伏在图3中消失，这显然是与原始数据在进行快速DCT变换后进行了量化有关，量化的过程将频谱的低频区域归零，起到了高通滤波的效果.从实际角度考虑，虽然损失了一些原始信息，但是有损压缩的优势依然明显.

5 结束语

在进行三维地质建模时，将静态图像的压缩技术应用于插值数据的压缩显然具有一定实际意义，针对大数据量的分批运算可以节省内存占用，而采用数据的压缩处理又可以节省磁盘占用，这样，原本需要多台计算机才能完成的超大处理工作可以优化为一台计算机来完成，从而节约了项目成本.

[1]徐能雄，段庆伟，梅钢，等.三维地质建模方法及程序实现.北京:地质出版社，2011.2.

[2]徐伯勋，自旭滨，于常青.信号处理及应用[M].北京:地质出版社，1997.

[3]胡广书.数字信号处理理论、算法与实现[M].北京:清华大学出版社，2003.8.

[4]Conzalez R C，Woods R E著.阮秋琦，阮宇智译.数字图像处理[M].北京:电子工业出版社，2003.

[5]陈普跃，赵新璧，陈斌.二维DCT快速算法及FPGA实现[J].电子质量，2008，2:5 －7.

[6]王新成，卢颉，朱维乐.二雏离散余弦变换一种新的快速算法[J]电子秤技大学学报，1993，22(6):561 －568.

[7]谢敏，黄贤武，等.一种快速DCT图像压缩算法的研究[U].计算机应用研究.2002:150－152.

[8]About Philips Trimedia SDE Reference I[Z].Philips，1998.

[9]马媛媛，杨峰，信科，等.基于DCT的J PEG图像压缩的研究[J].计算机技术与发展.2011.21(8):133 －136.

[10]曹雪虹，张宗橙.信息与编码论[M].北京:清华大学出版社，2009.