基于希尔伯特和傅立叶变换的笼型感应电动机转子断条故障检测
2013-09-26张惺
张 惺
(长沙电力职业技术学院,湖南长沙 410131)
0 引言
转子断条是笼型感应电动机的常见故障之一。当感应电动机发生转子断条故障时将导致电机出力下降,运行性能恶化,因此对其进行故障检测,特别是早期故障检测,对避免事故的发生,具有重要的意义。研究表明,当转子发生断条故障后,会在定子电流中出现频率为(1±2s)f1的电流分量,通过频谱分析来检测转子有无故障。由于定子电流信号易于采集,所以基于傅立叶变换的定子电流信号频谱分析被广泛的应用于转子断条故障的在线监测。当发生轻微故障时,分量的幅值相对于基频分量的幅值非常小,且由于电机转差率很小,使得(1±2s)f1与f1非常接近。在频谱图上,(1±2s)f1频率分量会因f1分量的泄漏而被淹没,使得灵敏度下降。为克服这些缺点,人们采取了自适应滤波法、派克矢量变换法、瞬时功率法、希尔伯特法等。
本文提出了基于希尔伯特变换和连续细化傅立叶变换的转子断条故障检测方法。基于感应电动机多回路数学模型进行数字仿真,仿真结果表明,该方法具有可行性。
1 基于希尔伯特变换和连续细化傅立叶变换的检测方法
1.1 希尔伯特变换原理
给定信号x(t),其希尔伯特变化定义为
正变换
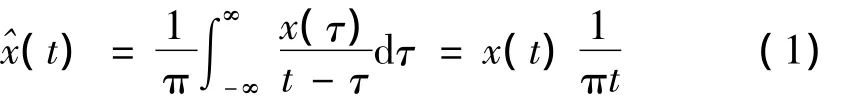
反变换
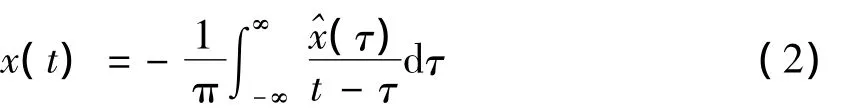
式(1)和式(2)称为希尔伯特变化对。

由上式可以看出,当信号经过希尔伯特变换后,幅值不变,负频率部分做90°相移,正频率部分做-90°相移。

该解析信号的幅值相位表达式为


希尔伯特变换的具体实现步骤是:首先对给定信号x(t)做正傅立叶变换得到X(f),然后对X(f)的正频率部分乘以-j,负频率部分乘以+j,得到(f),再对(f)做逆傅立叶变换得到(t)。
若x(t)为正弦(余弦)信号,则经过希尔伯特变换得到的信号幅值不变,只是相位移动了90°,变为余弦(正弦)信号。希尔伯特变换的实际就是对原信号进行90°的移相。在实际应用中,用移相来代替希尔伯特变换,可以减少计算量。
1.2 转子断条故障特征在希尔伯特调制信号中的表现
忽略高次谐波,发生转子断条故障时的感应电动机的定子电流为

式中,Im1、Im2—对应两个特征电流分量的幅值;φ1、φ2—对应两个特征分量的初相角;Im、φ—基频分量的幅值和初相角。
i1(t)经希尔伯特变换后,得

由此可得希尔伯特模的平方为
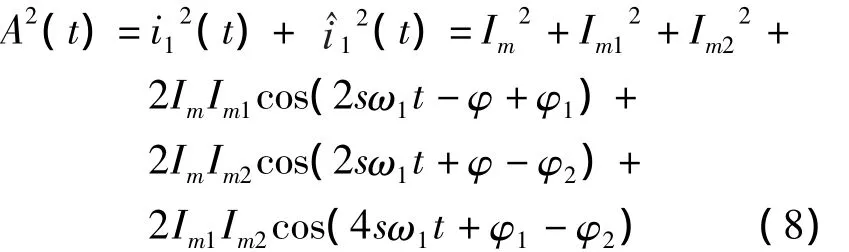
从式(8)中可看出,信号A(t)中含有直流、2sf1、4sf1频率分量,原电流中的基波分量转换成了直流分量,主要的故障特征分量转换成了2sf1分量。把2sf1作为转子断条故障的特征分量,根据频谱中是否包含2sf1分量来判断转子是否发生断条故障。但由于感应电动机运行时转差率很小,所以在频谱图中2sf1频率分量与直流分量非常接近,在做频谱分析时,2sf1频率分量可能被直流分量所淹没,从而给转子断条故障检测带来困难和误判,因此还需对信号进行滤除其直流分量然后再进行分析。
在信号中A(t)含有直流、2sf1频率分量,将2sf1频率分量作为转子断条故障的特征分量,直流分量就成了无用的噪声,应当滤除。在滤除直流分量的同时必须尽可能的减少2sf1频率分量的衰减,为实现上述目的,设计一个截止频率为1Hz的高通数字滤波器,其转移函数为

1.3 连续细化傅立叶变换技术
连续细化傅立叶变换是指应用连续的傅立叶变换频谱曲线,对快速傅立叶变换频谱在指定的区域内(如Δf频率间隔内),进行指定密度的细化。
对采用频率为fs,采样点数为N的时间序列i(tk),离散傅立叶级数为

快速傅立叶变换是离散傅立叶变换当N=2m时的特殊情况。此种变换,频率分辨单元为,与采样点数N成反比,若要提高频率分辨能力,则需减少分辨单元,成倍增加采样点数。当N一定时,频率分辨能力也就无法再提高。
时间序列i(tk)中含有从0频域信息,如果把频域曲线看成是连续的,也就是式(10)中的n看成是一个在区间内的连续实数,则式(10)变为

利用连续细化傅立叶变换技术,可以求出待分析信号中某一个主要频率分量的精确表达式,求得频率、幅值和初相角。应用连续细化傅立叶变换时,可逐级进行细化范围和密度,以提高计算速度。
1.4 基于希尔伯特和连续细化傅立叶变换的检测方法步骤
根据前面的理论分析,可归纳出基于希尔伯特变换和连续傅立叶变换的感应电动机转子断条故障在线检测的方法,步骤如下
(1)采集一相定子电流瞬时信号,记为ia;
(2)对ia作希尔伯特变换,求得a;
(3)构造一个新的复值信号,i(t)=ia(t)+ja(t),可求得希尔伯特模的平方为:A2(t)=
(4)利用式(10),滤掉A2(t)中的直流分量,结果记为A2(t)′;
(5)对A2(t)′作连续细化傅立叶分析,根据频谱图中是否包含2sf1分量可判断转子有无断条。
2 仿真分析
在Matlab环境下,基于多回路模型,对一台Y-160L-4型电机进行转子断条故障数字仿真。电机的主要参数如下,额定功率PN=15kW,额定电压UN=380V,额定电流IN=30.3A,额定转速nN=1 480r/min,极对数 p=2,定子槽数36,转子槽数26。
当转子导条一根断裂时,定子电流如图1所示。直接对定子电流进行FFT分析,如图2所示。故障特征分量容易被基频分量所淹没,很难判断故障是否发生。图3为经过希尔伯特变换滤掉直流分量后,希尔伯特模的频谱图。图4为对希尔伯特模进行频谱细化得到的频谱图。
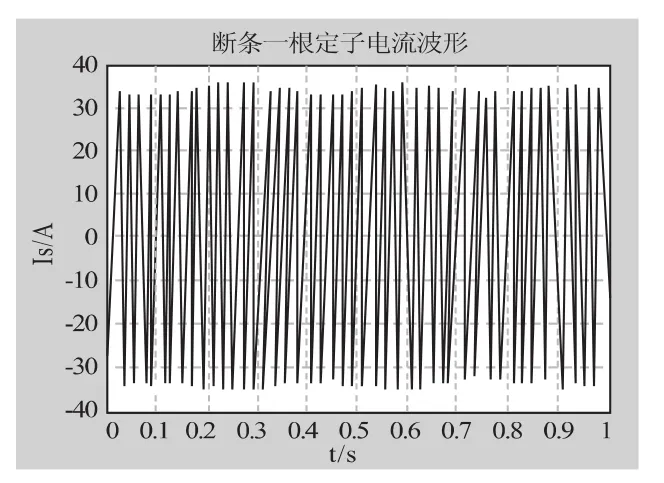
图1 定子电流图

图2 定子电流频谱图

图3 希尔伯特频谱图

图4 经过连续细化傅立叶变换的希尔伯特频谱图
3 结语
经过希尔伯特变换,滤波消除直流分量后进行连续细化傅立叶变换的仿真结果,能更加突出故障分量,从而提高了检测的灵敏度和可靠性。仿真证明,通过对定子电流做希尔伯特变换解调处理,再加以滤波和连续细化傅立叶变换处理,以调制信号的频谱图中是否存在故障特征量来判断转子是否发生断条是可行的,这种方法可以解决基频分量淹没边频分量以及负载波动对故障特征提取的影响。
[1]姜建国,汪庆生,杨秉寿,等.用自适应方法提取鼠笼式异步电机转子断条的特征分量[J].电工技术学报,1996,(4):176-179.
[2]邱阿瑞.用起动电流的时变频谱诊断鼠笼异步电机转子故障[J].中国电机工程学报,1995,15(4):267-273.
[3]邱阿瑞.提取感应电动机转子故障特征的新方法[J].清华大学学报:自然科学版,1997,37(1):35-37.
[4]A.J.Marques Cardoso,S.M.A.Cruz,J.F.S.Carvalho,et al,Rotor cage fault diagnosis in three-phase induction motors,by Park's vector approach[J].Proceedings of the 1995 IEEE IAS Annual Meeting,San Diego(USA),642-646.
[5]刘进明,应怀樵.FFT谱连续细化分析的富里叶变换法[J].振动工程学报,1995,8(2):162-166.
[6]Ganyun,Cheng Haozhong,Zhai Haibao,et al.Fault Diagnosis of Power Transformer Based on Multi-class SVM Classifier[J].Electric Power Systems Research,2005,74(1):1-7.
[7]许伯强,李和明,孙丽玲.小波分析应用于笼型异步电动机转子断条在线检测初探[J].中国电机工程学报,2001,21(11):24-28,33.
[8]Schoen R R ,Habetler TG,Kamran F.Motor bearing damage detection using stator current monitoring[J].IEEE Trans on Power Delivery ,1994 ,39(10):322-332.
[9]盛兆顺.设备状态监测与故障诊断技术与应用[M].北京:化学工业出版社,2003.
[10]马宏忠.电机状态监测与故障诊断[M].北京:机械工业出版社,2007.
[11]高景德,王祥珩,李法海.交流电机及其系统分析[M].北京:清华大学出版社,1993.
[12]沈标正.电机故障诊断技术[M].北京:机械工业出版社,1996.
[13]汤蕴璆,史乃.电机学[M].北京:机械工业出版社,1999.
[14]蒋建东,蔡泽祥.鼠笼型异步电动机转子故障诊断新方法[J].继电器,2004,32(7):14-16.
