基于有限元法的转向直臂锻件晶粒度预报
2013-09-26彭李静陈文琳王少阳
彭李静,陈文琳,王少阳
(1.广州海格通信集团股份有限公司,广州 510663;2.合肥工业大学材料科学与工程学院,合肥 230009)
金属热锻过程不仅使材料发生变形,同时通过动态再结晶、晶粒长大使锻件晶粒度发生变化。晶粒度是锻件质量指标之一,粗大的奥氏体晶粒不利于锻后热处理,难以得到细小均匀的组织[1]。汽车转向直臂是汽车转向系统中的关键零件,它连接车轮和车身,其质量直接决定着行车安全。在汽车行驶过程中,由于转向直臂承受着频繁而复杂的多变应力的作用,因此对它的强度要求比较高。该转向直臂使用42CrMo低合金钢生产,经金相检测发现,生产用坯料加热后的奥氏体晶粒尺寸为100 μm,必须通过合理的锻造工艺,使其晶粒尺寸减小到锻件质量标准要求。文中采用有限单元法,结合42CrMo动态再结晶模型,对汽车转向直臂热锻成形过程进行数值模拟,预报了热锻过程中晶粒度演化情况。结果显示,锻造完成后晶粒度由初始坯料的100 μm降低至30~50 μm,满足质量标准要求。通过检测实际锻件的奥氏体晶粒度,证明该预报模型具有一定的可靠性。
1 汽车转向直臂锻造成形工艺
汽车转向直臂的零件如图1所示,可以看出,锻件形状较简单,然而锻件沿长度方向各部分的截面尺寸分布不均匀,中间部位的弯曲弧度较大。该锻件的工艺路线为:电磁感应加热-制坯-终锻成形,其中制坯工步为镦粗头部-拔长杆部-弯曲,如图2所示。

图1 汽车转向直臂零件Fig.1 The steering arm
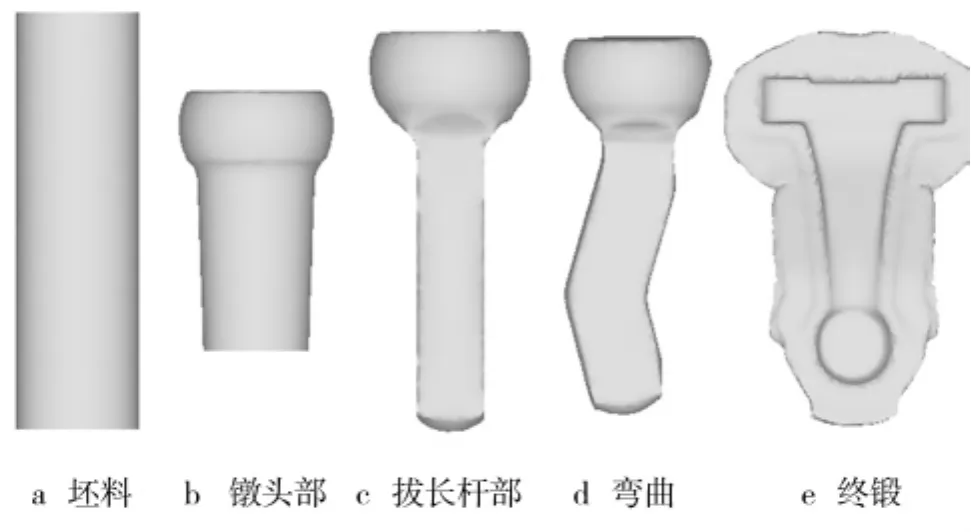
图2 工艺路线Fig.2 The Forging Process
2 汽车转向直臂热锻成形有限元模型
2.1 42CrMo动态再结晶模型
动态再结晶模型能够描述金属在不同变形条件下所得到的再结晶体积分数、平均晶粒度,Lin等对42CrMo的亚动态再结晶、动态再结晶模型进行了研究[2-4]:

式中:εp为峰值应力值对应的应变值;εc为开始发生动态再结晶时的应变值;·ε为应变速率;T为变形热力学温度;R为理想气体常数;d0为初始晶粒尺寸。
动态再结晶动力学方程如式(3)所示:

动态再结晶晶粒尺寸模型为:

式中:Xdrex为动态再结晶体积分数;ε0.5为动态再结晶体积分数在50%时的应变;ε为应变值;drex为动态再结晶晶粒尺寸。
2.2 热锻过程的有限元模型
坯料弯曲和终锻时建立的有限元模型如图3所示,工件材料为42CrMo,初始尺寸为φ65 mm×220 mm,初始晶粒度为100 μm。将上述动态再结晶模型及42CrMo本构模型插入到该模型中[5],设置坯料初始温度为1100℃,模具预热温度均为250℃,摩擦模型为常剪应力摩擦模型,摩擦因子取0.3,模锻速度为200 mm/s。锻造过程中各工步间的时间间隔假设为5 s,拔长各道次间隔为2 s。

图3 坯料弯曲和终锻时的有限元模型Fig.3 The FEM model during bending and final forging
3 模拟结果分析与讨论
按照如图2所示的锻造工艺,对工艺过程进行了数值模拟。结果显示,该工艺型腔充填完整,飞边尺寸均匀,成形性较好。此外,通过42CrMo动态再结晶模型,可以直观地观察锻造过程中晶粒度的演化过程。
3.1 镦粗对锻件微观组织的影响
转向直臂的横梁端展宽较大,坯料相应部位应进行镦粗,将坯料头部的100 mm高度镦粗至40 mm。镦粗后,坯料上各部分的动态再结晶体积分数分布如图4所示。动态再结晶体积分数由心部向外围逐渐减小,心部的动态再结晶体积分数最大,坯料头部顶端和杆部基本为0,不发生动态再结晶。分析认为,由于该工步为局部镦粗,变形主要集中在坯料头部,动态再结晶也主要集中在头部。另外,由于镦粗区域变形不均匀,也导致动态再结晶的程度各不相同。镦粗中心区为变形剧烈区域,再结晶体积分数最高,达到66%。由于两端的变形死区形变小,且与温度较低的模具接触,因此使得动态再结晶很难发生,再结晶体积分数基本为0。

图4 镦粗过程动态再结晶体积分数Fig.4 The dynamic recrystallization volume fraction during upsetting
由图5可见,坯料经镦粗变形后,头部金属的晶粒尺寸得到细化。由于动态再结晶不均匀,使得坯料头部各部分的晶粒尺寸值分布也不均匀。心部平均晶粒尺寸小,最小值为55.2 μm,晶粒细化程度达到44.8%,外围小变形区平均晶粒尺寸值为75.3~84.3 μm,难变形区及其附近的黏着区平均晶粒尺寸值与初始晶粒尺寸值相差不大,晶粒细化程度最小。
3.2 多道次拔长对锻件晶粒度影响
转向直臂的球头端和直臂部分的金属量分布少,需对坯料杆部进行拔长,将直径φ65 mm的圆截面拔长为45 mm×45 mm的矩形截面。坯料杆部长度仅为120 mm,采用自由锻整体拔长。

图5 镦粗结束后平均晶粒尺寸分布Fig.5 The average grain size during upsetting
坯料拔长过程实质上就是坯料的镦粗过程,同样存在着心部大变形区、外围小变形区及难变形区。坯料动态再结晶体积分数由内而外逐渐减小,心部大变形区的动态再结晶体积分数最高达到70%;坯料与模具接触的表层区域难以变形,动态再结晶体积分数最小。第2轮拔长过程中,由于工件翻转90°,使上一轮的难变形区成为可变形区。随着拔长的进行,变形程度也随着增加,再结晶体积分数逐渐增加。从整体上看,经第2轮拔长后,坯料杆部各部分区域均发生了不同程度的动态再结晶,这有利于均匀细化坯料晶粒尺寸。在第3轮拔长过程中,越来越多的表层金属发生完全动态再结晶,最终坯料上完全动态再结晶区域占总体积的3.91%,如图6所示,有利于坯料杆部金属的晶粒尺寸在整体范围内得到细化。

图6 拔长后坯料动态再结晶体积分数分布Fig.6 The dynamic recrystallization volume fraction during stretching
坯料杆部经3轮拔长之后即可达到形状及尺寸要求,增加翻转次数可继续均匀化再结晶体积分数的分布。同时,自由锻生产过程中应严格按照工艺步骤进行操作,否则可能导致动态再结晶不足。
拔长后坯料各截面上的平均晶粒尺寸分布如图7所示。随着拔长道次的增加,坯料平均晶粒尺寸值不断减小,由拔长前的90.9 μm减少到拔长后的61.7 μm,晶粒细化了36.22%。拔长道次对坯料平均晶粒尺寸的影响曲线如图8所示。可以看出,各轮拔长对坯料平均晶粒尺寸值的影响不一,与各轮拔长的压下量有关。4轮拔长的晶粒细化程度分别为8.03%,17.13%,6.36%,4.7%,起初的 2 轮拔长变形量大,晶粒细化程度也较大,随后几轮拔长的晶粒细化程度越来越小。坯料杆部经3轮拔长后,各部分晶粒尺寸逐渐趋于一致,最终晶粒尺寸值均为40~60 μm。

图7 拔长后坯料平均晶粒度Fig.7 The average grain size during stretching

图8 拔长道次对坯料平均晶粒尺寸的影响Fig.8 The influence of stretching passes on the average grain size of the billet
3.3 弯曲对锻件微观组织的影响
该锻件直臂部分存在着2个弯折点,且弯曲幅度大。通过预弯曲工序,可减少终锻时的金属流动,延长终锻模具的使用寿命。分别在变形体外表面及变形体内部沿轴线方向选定4个跟踪点,分析坯料弯曲过程中微观组织变化情况,如图9所示。

图9 坯料上跟踪特征点的位置分布Fig.9 The distribution of tracking points on the billet
弯曲过程中各跟踪点处平均晶粒尺寸的变化曲线如图10所示,弯曲过程中各点处的平均晶粒尺寸均减小。点1~8的平均晶粒尺寸值的细化程度分别为 10.18%,3.69%,4.64%,8.25%,10.85%,11.74% ,13.32%,11.55%,表明弯曲对坯料晶粒细化作用的影响较小。由于变形主要集中在坯料表层,尤其是点P1,P4,所以晶粒细化程度较高;点P2,P3变形小,且温度低,难于发生动态再结晶,晶粒细化程度小。坯料内部金属虽然等效应变值变化幅度不大,但变形温度高,易于发生动态再结晶,因而细化晶粒。
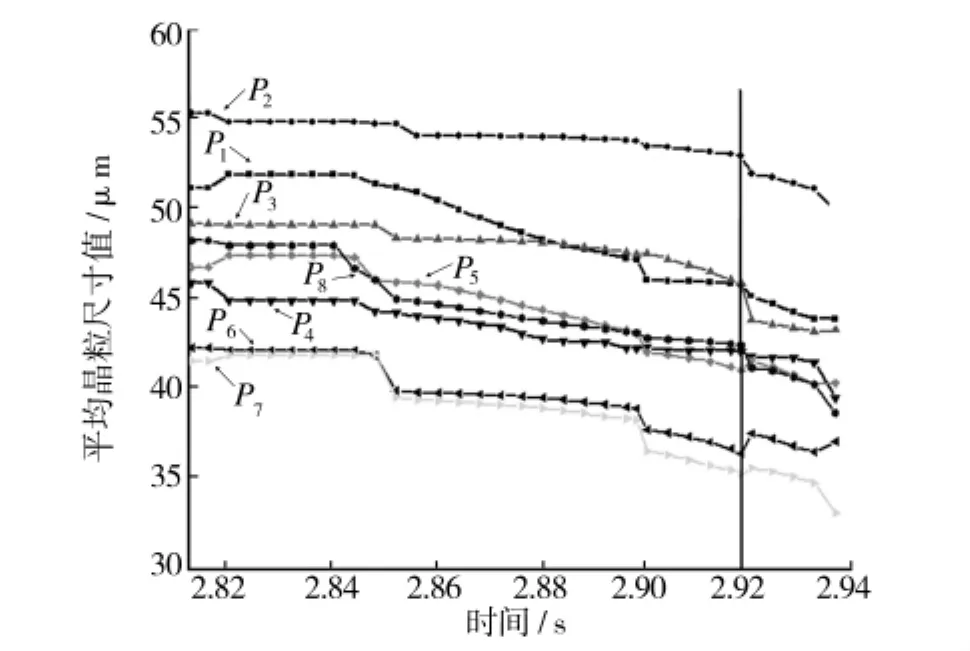
图10 弯曲过程中各跟踪点平均晶粒尺寸的变化Fig.10 The average grain size of the tracking points during bending
3.4 终锻成形对锻件微观组织的影响
转向直臂终锻成形后的动态再结晶体积分数分布如图11所示。经过终锻成形之后,锻件上有87%的区域发生了完全动态再结晶,动态再结晶体积分数平均值为0.974,锻件晶粒充分细化,性能也得到大大改善。如图12所示,锻件变形及晶粒尺寸分布不均匀,使得终锻件的平均晶粒尺寸值存在差别,杆部局部区域晶粒尺寸细小,需后续热处理工序使其充分均匀化。锻件平均晶粒尺寸为46.2 μm,相对于弯曲后晶粒尺寸,细化了23.5%。

图11 终锻成形结束时动态再结晶体积分数Fig.11 The average grain size after finish forging

图12 锻件终锻成形后的平均晶粒尺寸值分布Fig.12 The average grain size after finish forging
转向直臂工作时直臂部位为主要受力结构,该部位某截面上的动态再结晶体积分数分布如图13a所示,整个截面上各部分金属均发生了完全动态再结晶,锻件直臂部位的晶粒尺寸得到充分细化。锻件的平均晶粒尺寸分布如图13b所示,可见锻件截面上除靠近飞边部位的晶粒比较大之外,其余部位的晶粒均比较细小。根据动态再结晶理论可知,当应变达到临界值时,锻件就开始发生动态再结晶,晶粒得到细化。由于临近飞边部位的金属温度较高,容易导致已经细化了的晶粒发生二次长大,使得原本细化了的晶粒反而进一步粗化。此区域平均晶粒度约为30 μm,按晶粒度分级标准可达6.5级,满足锻件质量标准要求。

图13 某截面的再结晶情况Fig.13 The dynamic recrystallization of the discussion section
综上所述,使用该工艺成形的锻件,其平均晶粒度为46.2 μm,达到6级晶粒度标准;关键受力截面平均晶粒度可达30 μm,达到6.5级标准。坯料的粗大晶粒大大细化,符合锻件质量要求。同时,不同的制坯工艺对动态再结晶的产生、分布都有不同的影响,应当严格控制生产工序,保证锻件质量。
4 实验结果及分析
按照上述热锻工艺,作者针对转向直臂在某厂进行了试生产。终锻件模拟结果与实验结果对比如图14所示,终锻件能够良好成形。模拟得到的终锻件飞边形状与实际终锻件存在差别,主要集中在锻件直臂部位两侧的飞边。这可能是由于模拟过程中的网格重划分导致了三维模型体积减小;或者由于实际锻件的圆角稍大,因此其终锻模拟件飞边没有实际锻件大。另外试生产中,由于坯料摆放位置受工人操作的影响存在不稳定性,因此难免存在差别。总体分布状况基本类似,飞边金属主要分布在锻件直臂部位的两侧,头部和横臂部位的飞边金属较少,模拟结果具有可靠性。

图14 终锻件模拟结果与实验结果Fig.14 Simulation and experiment results of finish forging
锻件经切边、整形后,温度为850℃左右,直接淬火以保留其高温组织。得到的锻件实物如图15所示。在锻件直臂中段截取试样,用于观测锻件截面组织,如图16所示。各点处的金相照片如图17所示,可以看出,点A处的晶粒尺寸比点B处的晶粒尺寸小,即靠近飞边处的晶粒尺寸稍大。依据GB/T 6394-2002金属平均晶粒度测定法可评定,直臂中段部位的晶粒度达到6.5级,与模拟结果吻合。这表明该方案得到的锻件具有优良的内部组织以及较高的综合力学性能。

图15 转向直臂锻件实物Fig.15 Photo of the steering arm

图16 切取的试样及指定观测点Fig.16 The observing section and points

图17 各观测点处的金相照片Fig.17 Metallographic photo of the observing points
5 结语
不同的制坯工艺对锻件晶粒度分布有不同的影响,合理制定制坯工步,严格按工艺步骤生产,能够保证锻件的内在质量。此外,使用有限单元法,耦合了42CrMo动态再结晶模型的数值模拟方法,能够准确预报热锻过程中的晶粒度演化情况。根据有限元预报的结果,调整热锻工艺,能够避免重复实验,节约生产成本。
[1]吕炎.锻件组织性能控制[M].北京:国防工业出版社,1988:1-172.
[2]LIN Yong-cheng,CHEN Ming-song.Numerical Simulation and Experimental Verification of Microstructure Evolution in a Three-dimensional Hot Upsetting Process[J].Journal of Materials Processing Technology,2009,209(9):4578-4583.
[3]LIN Y C,CHEN M S,ZHONG J.Study of Metadynamic Recrystallization Behaviors in a Low Alloy Steel[J].Journal of Materials Processing Technology,2009,209(5):2477-2482.
[4]LIN Y C,CHEN M S,ZHONG J.Numerical Simulation for Stress/strain Distribution and Microstructural Evolution in 42CrMo Steel during Hot Upsetting Process[J].Computational Material Science,2008,43:1117 -1122.
[5]LIN Y C,CHEN M S,ZHONG J.Effect of Temperature and Strain Rate on the Compressive Deformation Behavior of 42CrMo Steel[J].Journal of Materials Processing Technology,2008,205(1/2/3):308 -315.
