基于改进型交叉算子的混合流水车间排序求解

黄宗南 张博凡 信宁宁

(上海大学机电工程与自动化学院，上海200072)

混合流水车间是指一批工件在流水线上进行多个阶段的加工，每一阶段至少有一台并行机器;在每一阶段各工件均要完成一道工序，各工件的每道工序可以在相应阶段上的任意一台机器上加工。这种形式的车间在制造业中比较常见，其作业排序比置换型车间更复杂。因此，为了提高企业设备的使用效率，科学合理的作业排序方法非常重要。

混合流水车间排序问题也是研究热点之一［1－4］，本文在前期的研究基础上，将提出的改进型单点交叉算子［5］扩展应用到混合流水车间排序问题中，并测试该算子的求解性能。

1 混合流水车间排序的数学模型

混合流水车间排序问题的数学描述如下:

符号和变量定义为:

N为工件数;S为加工阶段数(工序数);

M(k)为第k道加工工序的并行机器数量;Pik为工件i在第k道工序的加工时间;

Cik为工件i在第k道工序的完工时间;PN为足够大的正整数;

Yikm=1，表示工件i分配到第k道工序m机器上加工，否则Yikm=0;Xijk=1，表示工件i在第k道工序领先工件j加工，否则Xijk=0。

式(1)表示排序的目标函数，即要求工件加工最大完工时间最小化，也叫Makespan指标;

式(2)表示各工件在每一道工序只能分配一台机器加工;

式(3)表示每一工件须经S道工序加工;

式(4)和(5)表达了同一工序同一机器上不同工件加工顺序约束，保证一台机器在同一时刻只能加工一个工件;

式(6)描述了每一工件须依次在不同工序加工的顺序要求，保证一个工件同时只能在一个工序加工;

式(7)和(8)为决策变量和参数取值约束。

2 混合流水车间排序问题求解

2.1 遗传寻优流程

图1是求解混合流水车间排序问题的遗传算法操作流程。

第一步，随机生成N个个体组成初始种群。其中，每个个体表示染色体的基因编码，对于混合流水车间排序问题，常用的编码方式有矩阵编码、复合编码和置换编码等。本文采用置换编码。例如，对于5个工件的混合流水车间排序问题，假设一条染色体为［2 4 1 5 3］，则表示工件进入流水线的顺序为“工件2→工件4→工件1→工件5→工件3”。

第二步，解码。对于采用置换编码的混合流水车间排序问题，需要同时安排设备的分配和工件的排序。本文采用基于 FIFO(先进先出)［6］的解码方式。例如，设有m个工件，S道工序，每道工序有M(s)台并行机器，并且已知工件在每台机器上的加工时间，解码的操作流程为:把前工序最早完工的工件依次分配给当前工序的机器上，空闲的机器数由每道工序的并行机数量以及当前已分配任务情况决定，一台机器同一时刻只能加工一个工件，按这样的操作从第一道工序直至最后一道工序进行解码，确定各工件在机器上的加工顺序。

第三步，计算个体的适应度。根据遗传算法目标函数的方向与适应度值变化方向相同的原则，本次采用的适应度函数为式(1)目标函数的倒数。

第四步，进行遗传操作，即进化寻优。

①选择操作。本文采用与生物自然选择最相似的轮盘赌选择算子，用正比于个体适应度值的概率来选择个体。

②交叉操作。采用改进型单点交叉算子，此操作方法在下节中展开。

③变异操作。常用的变异方法有交换变异、倒位变异、插入变异等。本文采用交换变异。例如一条染色体为［2 4 1 5 3］，随机选取第2和第4位置，则交换变异的结果是［2 5 1 4 3］。

2.2 改进型交叉算子

由前期研究可知，改进型单点交叉算子性能良好［5］，故将该算子扩展应用到混合流水车间排序问题。以两个父代［9 7 4 1 8 6 5 3 2］和［9 6 1 4 3 8 5 7 2］为例，改进型单点交叉算子的操作过程如图2。

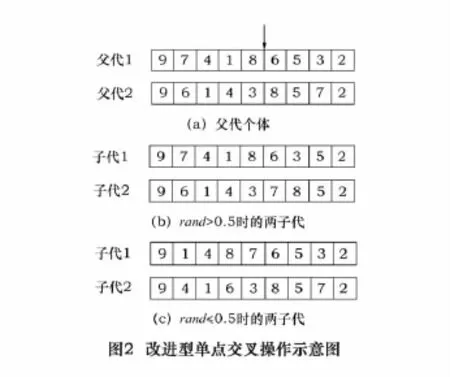
(1)产生一随机数(rand)，当随机数大于0.5时，把两父代交叉点前的基因复制给子代，然后从父代2(或1)中找出子代1(或2)中缺失的基因，并将其按顺序复制给子代交叉点后的位置。得到的子代见图2b。

(2)当随机数小于等于0.5时，把两父代交叉点后的基因复制给子代，其余操作与步骤1类似。得到的子代见图2c。

从上述操作结果可知，对于二进制编码，改进型单点交叉保留交叉点前或交叉点后的基因所得到的子代是相同的;而对于符号编码，由于染色体中会出现重复基因是非法的，故需要对重复基因进行替换，所以保留交叉点前或交叉点后的基因所得到的子代是不同的。与典型单点交叉相比，改进型单点交叉扩大了染色体基因的改变范围，增大了搜索空间。

根据计算流程用Matlab语言编制了求解该问题的遗传算法程序，实现混合流水车间排序问题的求解。

3 实验分析

实验采用文献［7］中的案例。某汽车发动机厂加工车间要加工12个工件，每个工件有车、刨、磨3道工序，现有3台车床完成工序1，2台刨床完成工序2，4台磨床完成工序3，每台机床的加工能力不同，具体加工时间如表1所示［7］。

表1 工件在每台机床上的加工时间

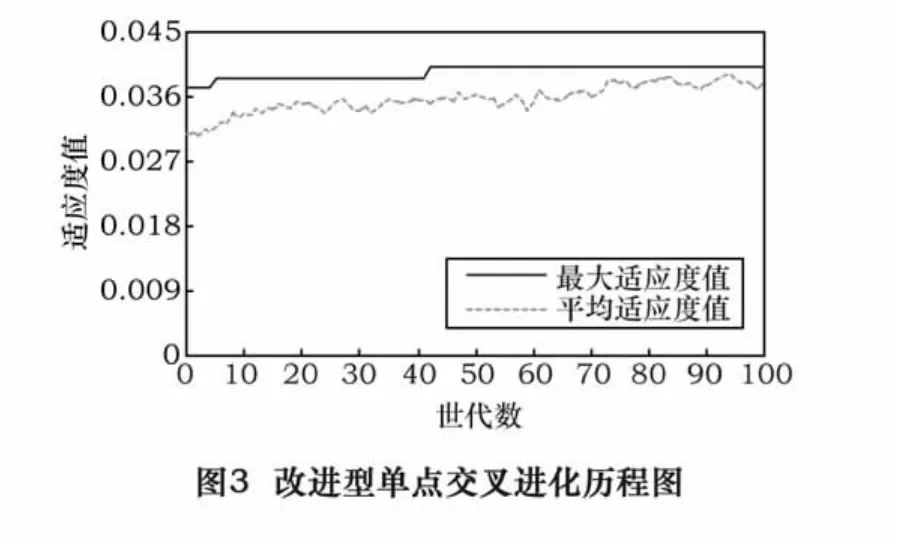
在计算实验时，遗传参数设置与文献中相同:种群个数30，交叉率0.8，变异率0.05，进化代数100。经过多次运算，［4 11 6 1 12 2 3 10 5 9 8 7］是得到的最好的染色体之一，其进化历程图如图3所示。同时，与典型单点交叉算子进行比较，典型单点交叉算子的进化历程图如图4。

从以上两个进化历程图可以看出，进化前期两个算子的平均适应度都在增加、进化，但改进型单点交叉算子比典型单点交叉算子速度更快;进化的后期虽然都逐渐趋于收敛，但改进型单点交叉算子更稳定。观察最大适应度曲线，改进型单点交叉算子能够更快找到最优解。由此可知，改进型单点交叉算子的整体寻优过程更好。

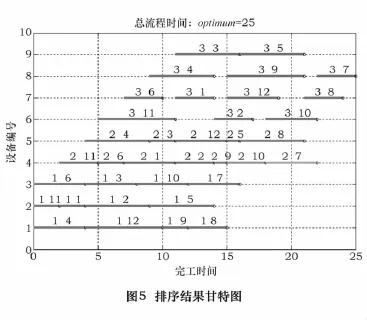
据此，最优排序的甘特图如图5，该方案的最大流程时间为25个单位。图中的线段表示工件的加工时间，线段上方的第一位数字代表工序号，第二位数字代表工件号。从图中排序结果可以看出，各并行机器被分配的加工任务比较均匀，且各机器在加工时间上基本保持连续，机器的空闲时间少，使完工时间减少。

为了进一步确认算法的有效性，与两个文献中该案例的实验结果进行比较，实验结果见表2。

由表中数据可知，本方法所求得的最好解为25，好于文献［7］中的29和文献［8］中的26;平均值为26，同样优于文献［7］中的29.4和文献［8］中的27.2;说明本研究采用的变形遗传算法求解性能良好。

表2 实验结果统计(10次运算)

4 结语

将改进型单点交叉算子扩展应用到混合流水车间排序问题中，并对其求解性能进行测试。结果表明算法求解性能良好。

［1］唐立新，吴亚萍.混合流水车间调度的遗传下降算法［J］.自动化学报，2002，28(4):637 －641.

［2］Bassem Jarboui，Mansour Eddaly，Patrick Siarry.A hybrid genetic algorithm for solving no－ wait flowshop［J］.Intermational Journal of Advanced Manufacturing Technolgy，2010(11):472－478.

［3］王万良，姚明海，吴云高，等.基于遗传算法的混合Flow－shop调度方法［J］.系统仿真学报，2002，14(7):863 －869.

［4］胡燕海，严隽琪，叶飞帆.基于遗传算法的混合流水车间构建方法［J］.中国机械工程，2005，16(10):888 －891.

［5］张博凡，黄宗南.基于变形遗传算法交叉算子的Flow－Shop问题求解［J］.制造业自动化，2011，33(10):27 －29.

［6］王凌.车间调度及其遗传算法［M］.北京:清华大学出版社，2003.

［7］吴云高.基于遗传算法的车间调度方法及其应用［D］.杭州:浙江工业大学，2002.

［8］周辉仁，唐完生，魏颖辉.基于微粒群算法的柔性流水车间调度优化［J］.中国机械工程，2010，21(9):1053 －1057.