基于遗传算法的航班着陆调度的设计与实现
2013-09-25张子阳张晓玮郝宾宾张启升
张子阳 , 张晓玮 , 何 彬 , 郝宾宾 , 张启升
(1.地下信息探测技术与仪器教育部重点实验室 北京 100083;2.中国地质大学(北京)地球物理与信息技术学院,北京 100083;3.中国地质大学(北京)信息工程学院,北京 100083)
航班着陆调度是机场管理的重要组成部分,旨在为待着陆的航班安排合理的着陆调度方案,保证机场的秩序,减少早到或者晚到造成的经济损失。因此研究航班的调度问题对提高机场的运行效率以及飞行效益具有重大意义。着陆调度问题是一个典型的组合优化问题[1],其可能的排序数随着航班数量的增多而呈指数型增长,属于NP-hard问题,而且此问题还涉及各种限制条件[2],比如机型,飞速,风速,突发状况等,导致其带有有限数量的可行解。
目前许多学者提出了解决航班调度的方法,Beasley J E等[3]通过建立混合整数线性规划模型,用分支定界法求解,Hu等人[4]在文献中采用了基于二进制表达的遗传算法解决了机场调度问题,Beasley J E[6]等运用人口启发式算法来解决航班调度问题,Cheng V H L[7]等通过遗传搜索技术解决了航班着陆调度问题,Chou等人[5]采用基于不均等策略的多目标遗传算法解决了航班着陆安排问题,Xu Xiaohao等[8]和John E[9]都采用模糊算法来对航班调度问题求解。文中介绍了静态航班调度模型和先来先服务的动态航班调度模型,并在此基础上设计和实现了基于遗传算法的航班着陆调度模型。
1 航班着陆调度模型
1.1 静态模型
航班着陆调度是指针对给定的待降落航班队列,在满足各种约束条件的情况下对其中的航班进行排序并且给出一个高效合理的调度方案,包括着陆的次序和时间。约束条件包括航班的时间窗限制和航班之间的最小安全间隔的限制。
首先每个航班必须在特定的时间窗内降落,它由最早降落时间和最迟降落时间决定,最早降落时间是指航班以其最大飞行速度飞行的降落时间,最迟降落时间主要考虑到航班携带的燃料量。其次从空气动力学考虑,任意两家航班降落之间都应该满足最小安全时间间隔的约束。如果某个航班在飞行过程中产生大尾流,导致后面离的太紧的航班失去平衡,就可能造成航班事故。航班调度的约束示意图如图1所示。
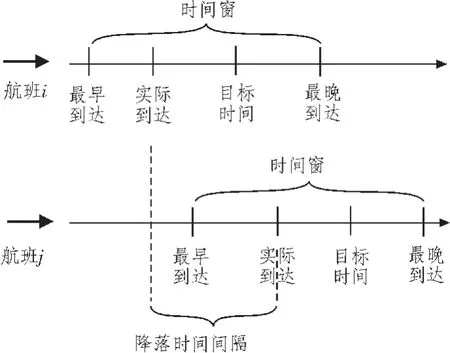
图1 航班调度的约束示意图Fig.1 Diagram of the flight scheduling
假设有n架航班进入终端区,TEi代表航班最早到达时间,TLi代表航班最晚到达时间,TAi代表航班实际到达时间,TXi代表航班目标到达时间,Sij代表航班i和航班j降落的最短时间间隔,PUi代表早到或者晚到单位时间的惩罚值,PUS代表总的惩罚值。
由此可知,航班 i的时间窗是[TEi,TLi],由于实际降落时间要在其时间窗内,所以约束条件必须满足:

对于任意两个航班,假设航班i在航班j之前降落,则其时间隔约束为:

从给出的时间窗口的角度分析,航班没有在目标时间到达的,会有惩罚,这个惩罚值就是每分钟的惩罚值乘以到达的时间与目标时间的间隔,把每架航班的惩罚值加起来就得到了总的惩罚值,也就得到了目标函数:
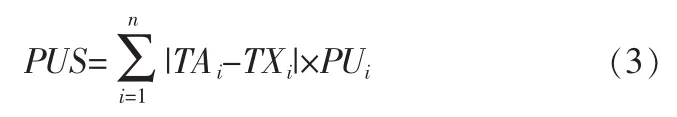
1.2 动态模型
动态模型是一个离散事件系统(Discrete Event System)模型,只有当一架航班到达终端区后,航班的排序队列才会发生变化。动态模型对航班队列进行重排可以分为以下3个步骤:首先,把新的航班加入到已经排好的队列尾端;其次,已经到达机场着陆的航班从队列中删除;更新后的队列按照静态算法重新排列。
先到先服务模型是一种经典的动态排序模型,其基本思想类似于贪心算法的思想:假设有n架航班,首先根据这n架航班的目标时间按照从小到大的顺序来排序得到航班序列(a1,a2,…,ai,…,an),然后基于先到先服务的思想,则排在第一位的航班就要先到达,并且基于贪心的思想是要让第一个航班的惩罚值最小,也就是说应让第一个航班在目标时间准时到达:

下一架航班到达后要考虑它的目标时间和第一架航班的时间间隔,由此得到第二架航班的实际到达时间为:
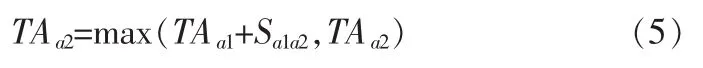
由此推广可以得到其他航班的实际降落时间的表达式:
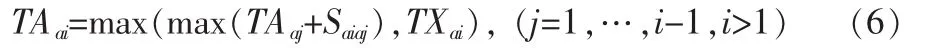
其算法流程图如图2所示。
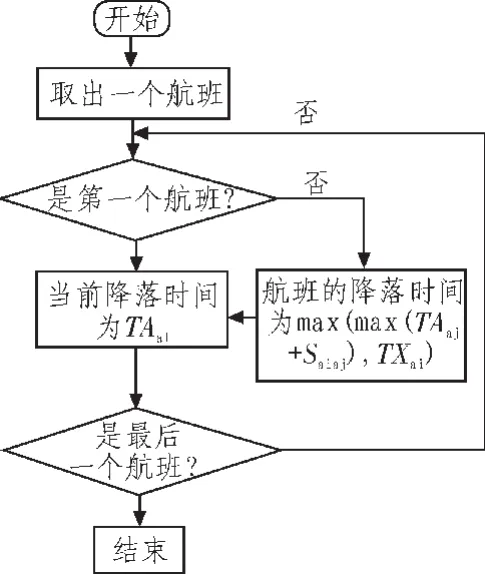
图2 先来先服务算法的流程图Fig.2 Flow chart of the first come first service algorithm
2 遗传算法的设计与实现
目前在航班的调度问题中,很多智能算法得到了一定的应用。原因是调度问题本身有很多的限制条件,而且要求解决方案具有较强的时效性和动态性。而传统的方法对于这类问题要么是束手无策,要么有很强的局限性而只能给出部分条件下的最优解,不具有全局性。遗传算法是一种应用比较广泛的智能算法,它是一类借鉴生物界自然选择和自然遗传机制的随机搜索算法,非常适用于组合优化等问题。该模型提供了求解非线性规划问题的通用框架,从随机产生的通用解开始搜索,通过一定规则的选择、交叉和变异操作逐步迭代以产生新的解。群体中的每个个体代表问题的一个解,称为染色体,染色体的好坏通过适应度值来衡量,根据适应的好坏从上一代中选择一定数量的优秀个体,通过交叉变异形成下一代个体。经过若干代的进化之后算法收敛于最好的染色体。系统的遗传算法的简化流程如图3所示。
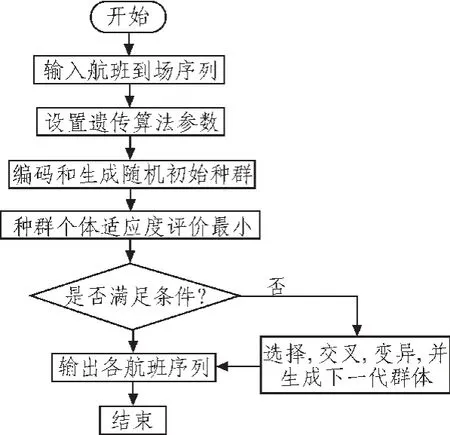
图3 遗传算法的流程图Fig.3 Flow chart of the genetic algorithms algorithm
2.1 编码方法
由于遗传算法不能直接处理问题空间的参数,因此必须通过编码把所求问题的可行解表示为遗传空间的染色体或者个体。其编码方法分为二进制编码方法,整数编码方法,实数编码方法和一般数据结构编码方法。基于航班调度问题的特点,采用实数编码方法即数字序号编码方法。每架航班bi代表一个基因值i,各航班序号排列成一个序列,即代表一种调度方案。如染色体2 3 1 6 4 5,代表航班 2为第一个着陆,3,1,6,4,5依次着陆。 此编码方法中实数代表个体基因型,航班的序列代表个体的表现型,两者是一一对应关系。
2.2 适应度函数
问题求解的目标函数与适应度函数一般有一定的关系。航班着陆调度问题是求目标函数的最小值,因此将函数的倒数作为个体的适应度值。目标函数值越小的个体其适应度越大,个体越优。因此染色体x对应的适应度函数为:
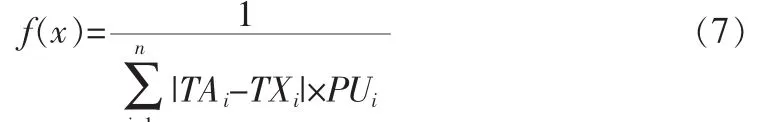
i=1
2.3 遗传算子
2.3.1 选择算子
选择操作是从上一级的数据中以一定的概率选择优良个体组成新的种群,并且繁殖得到下一代个体,其目的是使对生存环境适应度高的物种将有更多机会将优良基因复制到下一代,文中采用Holland提出的具有随机采样特点的轮盘赌选择。其原理是如果某个个体i的适应度为Fi,那么其被选择的概率为:
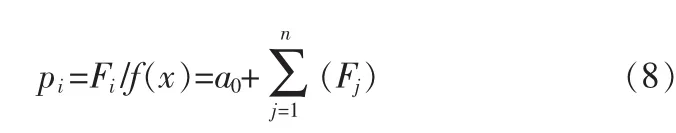
2.3.2 交叉算子
交叉操作是指从种群中随机选择两个个体,通过给染色体的交换组合,把父代的优秀特征传给子串,从而产生新的优秀个体。由于个体采用实数编码,所以交叉操作采用实数交叉法。先产生0到1的随机数b,则第k个染色体ak和第l个染色体a1在j位的交叉操作方法为:

2.3.3 变异算子
变异操作是为了改善遗传算法的局部搜索能力,避免陷入局部最优解,同样是保持群体多样性的重要手段。从种群中随机选取一个个体,选择个体中的一点进行变异操作,以便产生更加优秀的个体。amax是基因aij的上界,amin是aij的下界,f (g)=r2* (1-g/Gmax)2,r2是一个随机数,g 是当前的迭代次数,Gmax是最大进化次数,r为0到1区间产生的随机数。第i个个体的第j个基因进行变异操作的方法为:
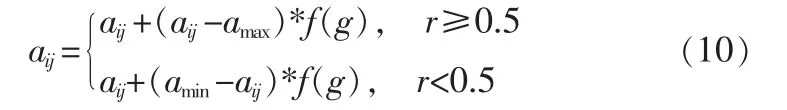
2.4 约束条件的处理
由于航班着陆调度受到航班的时间窗限制和航班之间的最小安全间隔的限制。文中采用罚函数处理约束条件[10]。由于航班i与航班j的最小着陆间隔为Sij,我们采用增加延误时间作为罚函数,对不满足约束条件的航班增加2Sij的延误。设航班i的原本延误时间为Li,若不满足约束条件,则罚后的延误时间为 Li’,Z代表符合约束条件的集合,则:
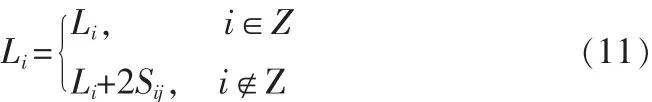
2.5 非线性寻优
遗传算法每进行一定的代数以后,以所得到的结果为初始值,采用Matlab2012优化工具箱里的线性规划函数fmincon进行局部的寻优,并将寻到的局部最优值作为新个体的染色体继续优化。
3 仿真结果与分析
采用Matlab2012编写遗传算法程序,以10架航班时刻表(表1)为原始数据,采用了传统的先到先服务(FCFS)算法和本文的遗传算法进行测试和计算,得出实际到达时间以及惩罚费用,并对其进行分析。根据计算,采用FCFS算法计算出的惩罚费用为1 210元,而采用遗传算法通过设置不同的参数经过多次网络培训之后,得到最优的一组解,其损失费用为823元。算法的个体数目为20,最大遗传代数为100,代沟为0.95,交叉概率为0.5,变异概率为0.02,分配适应度为函数值的倒数,训练10次。得到的遗传进化曲线图如图4所示,仿真结果如表1所示。
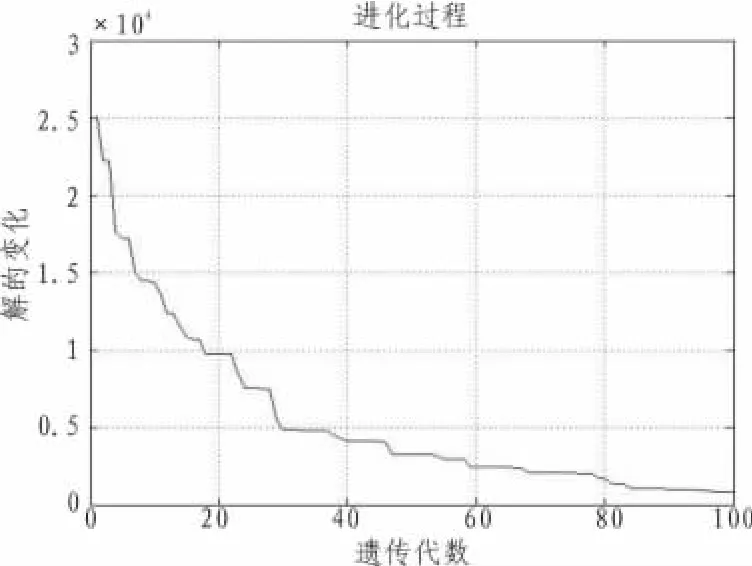
图4 遗传进化曲线图Fig.4 Diagram of the genetic evolution
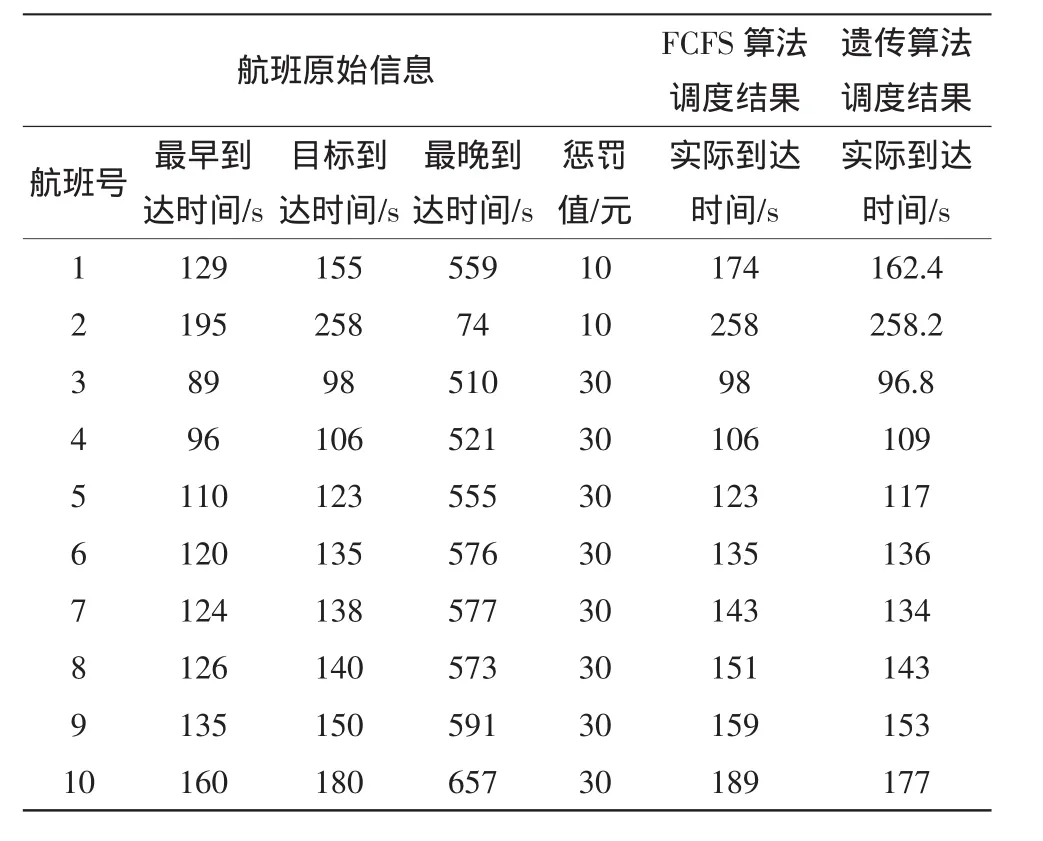
表1 仿真结果表Tab.1 Chart of simulation results
从仿真结果可以看出,采用遗传算法能够很好满足航班调度之间的约束条件,与传统的FCFS方法的调度结果相比,其惩罚总费用明显减少。可见该算法在约束条件下得到了损失费用相当少的多种优化方案,这就为工作人员在其他的约束条件下提供了更多的选择,从而有利于该模型的推广,具有更广的使用空间。
4 结 论
文中对航班着陆调度问题进行了探讨和分析,并采用遗传算法通过Matlab2012编程对其进行求解。仿真结果表明采用遗传算法进行优化,能够在满足约束条件下给出有效合理的次序和时间,相对传统先到先服务算法,明显减少了惩罚费用和延误时间。此算法设计合理,实现简单,能适应不同的约束情况,具有很高的实用价值。
[1]程晓航,薛惠锋,洪鼎松,等.进港航班调度的精华自适应遗传算法[J].交通与计算机,2006,24(6):91-94.
CHENG Xiao-hang,XUE Hui-feng,HONG Ding-song,et al.Design of elitist adaptive genetic algorithm in arrival aircrafts schedul ing[J].Computer and Communication,2006,24(6):91-94.
[2]张伟,王宏.求解机场终端区航班着陆调度问题的遗传算法[J].计算机工程与应用,2012,48(12):229-232.
ZHANG Wei,WANG Hong.Genetic algorithm on scheduling aircraft landing in aircraft terminal area[J].Computer Engineering and Applications,2012,48(12):229-232.
[3]Beasley J E,Krishnamoorthy M,Sharaiha Y M,et al.Scheduling aircraft landings the static case[J].Transport Science,2000(34):180-197.
[4]HU Xiao-Bing,Di P E.Binary-representation-based genetic algorithm for aircraft arrival sequencing and scheduling[J].IEEE Trans on Intelligent Transportation System,2008,9(2):301-310.
[5]Chou Ta-Yuan,Liu Tung-Kuan,Lee Chung-Nan,etal.Method of inequality-based multi objective genetic algorithm for do-mestic daily aircraft routing[J].IEEE Trans on Systems,Man, and Cybernetics A:Systems and Humans,2008,38(2):299-308.
[6]Beasley J E,Sonander J,Havelock P.Scheduling aircraft landings at London Heathrow using a population heuristic[J].Journal of the Operational Research Society,2001(52):483-493.
[7]Cheng V H L,Crawford L S,Menon P K.Air traffic control using genetic search techniques[C]//Proceedings of the 1999 IEEE International Conference on Lontrol Applications,1999(1):249-254.
[8]XU Xiao-hao,HUANG Ba-jun.Study of fuzzy integrated judge method applied to the aircraft sequencing in the terminal area[J].Acta Aeronautica et Astronautica Sinica,2001,22(3):259-261.
[9]John E.Fuzzy reasoning-based sequencing of arrival aircraft in the terminal area[C]//AIAA Guidance,Navigation and Control Conference, New Orleans, LA,1997:1-11.
[10]玄光男,程润伟.遗传算法与工程优化[M].北京:清华大学出版,2002:26-29.
