基于动态补偿的在线LS-SVM逆控制

颉 炯

（天水电气传动研究所有限责任公司，甘肃天水 741020）

1 引言

由于实际系统中总是存在参数的变化和外界干扰，这些不确定项的存在会对实际的控制系统产生影响，有时甚至会使控制系统发散，因此设计控制系统时要考虑其鲁棒性［1］。

直接逆模型控制［2-3］是一种简单有效的控制器设计方法，使用被控对象传递函数的逆模型作为串行控制器来开环控制系统的动态性能。文献［2］采用最小二乘支持向量机(Least Square Support Vector Machine,LS-SVM)对系统进行逆建模，将逆模型作为串行控制器对被控系统进行开环控制，并对几种典型信号进行了跟踪仿真，但文中未考虑系统的参数变化和外界干扰。文献［3］针对开环逆控制，在核函数为Lipschitz的条件下，证明了LS-SVM逆控制器是有限增益稳定的，但文中也未涉及到系统发生参数变化和存在外界干扰时的稳定性问题。因此当系统参数变化和存在外界干扰时如何提高直接逆控制器的鲁棒性以及如何尽可能准确地构造被控对象的逆模型成为直接逆控制需要解决的关键问题。支持向量机是一种基于结构风险最小化的机器学习算法，可以逼近任意一类非线性函数。而最小二乘支持向量机是采用二次规划方法解决函数估计问题的方法。该方法计算简单，收敛速度快，精度高，在函数估计和控制中得到广泛应用［4-8］，为逆系统控制方法中构造逆系统模型提供了理论依据。

基于此本文引入LS-SVM离线建立被控系统的逆建模，并借助无模型自适应控制思想［9-10］，设计一个补偿控制器，作为系统参数发生变化时的逆模型控制的补偿控制，同时引入系统控制误差ε不敏感函数，当系统控制误差超出不敏感区域时，利用增量算法对逆模型进行在线修正，提高控制精度。仿真结果表明文中所提方法能有效地增强控制器的鲁棒性和控制精度。

2 最小二乘支持向量机

2.1 批量LS-SVM函数估计算法

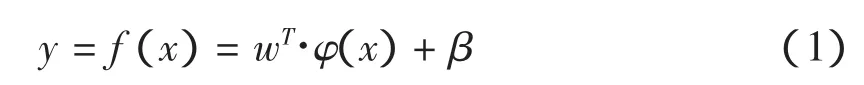
其中：w为权向量，β为偏移量。

在LS-SVM中，目标函数描述为：

式中：J为优化目标函数；γ为正则化参数；ek为误差变量。

约束条件yk＝wT·φ（xk）+β+ek（k＝1，2…N），定义拉格朗日函数为：

式中：αk为拉格朗日乘子，根据Karush-Kuhn-Tucker（KKT）最优条件［7］：

从而求解的优化问题转化为求解线性方程组问题

式中：α＝［α1，…，αN］T，1＝［1，…，1］T，y＝［y1，… yN］T，I为N×N辨识矩阵，Ω为核矩阵，Ωij＝K（xi，yj），K为定义的核函数。

将式（4）简化为：

选择满足Mercer条件的核函数

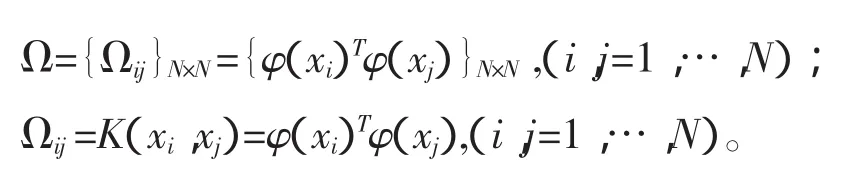
本文中核函数选取径向基函数

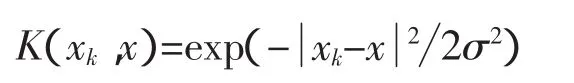
式中：σ为一正的实常数,表示核宽度。

非线性回归函数就可以表示为：

2.2 LS-SVM增量算法

令（xN+1，yN+1）为一组新的训练数据，由式（5）得原模型与新模型的增量关系为：

式中：

其中：c＝γ-1+φN+1φN+1a ＝［1 φ1φN+1φ2φN+1… φNφN+1］

由矩阵逆定理可得：

式（8）可减少求解大规模逆矩阵的时间。

3 基于动态补偿的在线LS-SVM逆控制

3.1 LS-SVM逆控制

考虑SISO非线性离散系统

y（k+1）＝f［y（k），…，y（k-n），u（k），…，u（k-m）］（9）式中：u（k）、y（k）分别为输入、输出量，则 u（k）的显示表达式为：

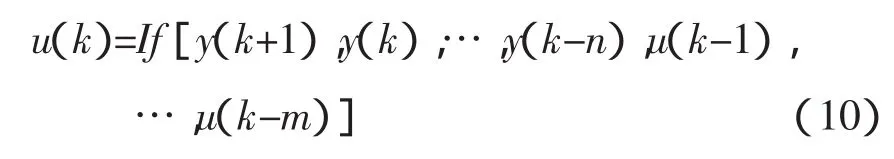
令参考输入φ（k）＝y（k+1），则式（10）可以表示为：

由于式（10）在工程实际中常常难以确切描述,本文拟采用LS-SVM逼近系统（9）的逆模型，即式（11）的逼近式。可以表示为：

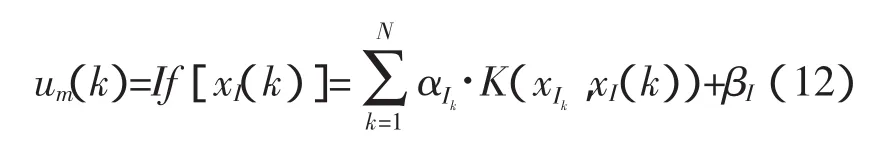
其中 u-＝［u（k-1），u（k-2），…，u（k-m）］

y-＝［y（k-1），y（k-2），…，y（k-n）］

y+＝［y（k+1），y（k）］

通过LS-SVM学习，利用已知数据建立系统的逆模型，其结构如图1所示。

图1 基于LS-SVM的逆模型

3.2 无模型自适应控制方法

无模型自适应控制方法（MFAC）中控制器的设计不需要受控过程的数学模型结构及辩识过程，不需要针对某个特定的受控对象进行控制器设计，也无需对控制器参数进行复杂的人工整定，并且有一定的系统稳定性分析来保证系统的闭环稳定。

本文将MFAC用于在线LS-SVM逆控制的补偿控制，用以克服实际系统中时变参数摄动或不确定。

以下给出非线性系统（9）基于紧格式线性化的MFAC控制方案［9］：

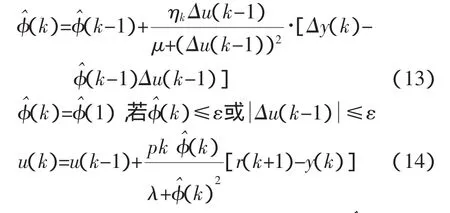
其中pk、ηk为步长序列，且pk，ηk∈（0，2）。（k）为基于紧格式线性化的伪偏导数μ为关于参数估计变化量的惩罚因子；λ为权重因子，作用是限制Δu（k）；ε为一个充分小的正数的初值；r（k）为参考轨迹。

从上述控制方案可以看出MFAC方法不包含系统辩识这个环节，仅用受控系统的I/O数据，与受控系统的数学模型和阶数无关，而且MFAC算法简单，计算量小。

3.3 基于动态补偿的在线LS-SVM逆控制

由于参数摄动和外界干扰的存在，可能会导致控制系统性能下降，甚至造成系统不稳定。因此设计一个补偿控制器uc（k）来改善控制系统的性能，修正的控制器为：

其中：um（k）为基于标称系统所设计的控制器。

在线LS-SVM逆控制即在标称系统下所设计的，式（12）是在标称情况下通过训练得出的，也可表示为：

因为MFAC方法不包含系统辩识部分，仅用受控系统的I/O数据，而且MFAC算法简单，计算量小，所以本文中的补偿控制器uc（k）借助MFAC算法来实现。将MFAC改进用于动态补偿的算法如下：

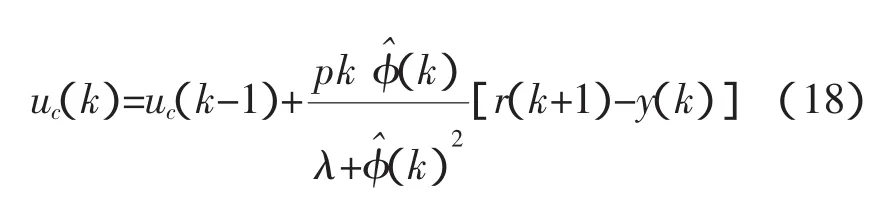
考虑到系统参数的时变摄动，将系统实际输出与参考输入的误差作为控制性能的评价指标，引入控制误差ε不敏感函数，利用增量算法对逆模型进行在线学习，减小计算的复杂度，提高实时控制性能和精度，同时提高控制器的鲁棒性。基于动态补偿的在线LS-SVM逆控制框图如图2所示。

图2 基于动态补偿的在线LS-SVM逆控制框图

根据离线逆控制器的设计，基于系统控制误差的ε不敏感函数的增量算法，实现在线训练步骤如下。

步骤1初始化在线模型，即利用已知数据训练得到被控系统的离线逆模型。

步骤2设r（k+1）为下一时刻的参考输入，由式（15）可得被控对象的控制量u（k）。由被控对象实际输出y（k+1）和参考输入r（k+1）得系统控制误差：

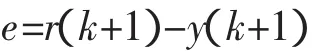
步骤3根据不敏感函数确定系统控制误差

步骤5 由式（6）和式（7）可得到在线模型参数αN+1更新逆模型，并作为下一时刻的初始化模型。返回步骤2。

4 仿真研究

考虑如下非线性离散系统

其中：a、b、c均为0.3；d（k）为外界干扰。假设系统的参考轨迹为：

4.1 逆系统模型的建立

采用LS-SVM逆系统建模方法对系统（19）离线建立其对应的逆模型作为直接逆控制器，如图3所示为LS-SVM逆模型辨识仿真曲线。从图3可知，LS-SVM能很好地逼近逆系统。

图3 LS-SVM逆模型辨识

4.2 在线LS-SVM逆控制器和补偿控制器的设计

为充分激励被控系统，控制量u取幅值为2.0的正弦信号，采集300组数据进行系统逆模型的建立，用交叉验证方法选取模型参数。将离线建好的逆模型作为逆控制器（式16）串联在被控系统的前面，将系统实际输出与参考输入的误差作为控制性能的评价指标，引入控制误差ε不敏感函数，即当系统误差超出不敏感区域时，利用LSSVM增量算法对逆模型进行在线修正，保证系统的控制精度。

补偿控制器中参数的设计如下，设置步长序列pk＝1.9，ηk＝1.9，参数估计变化量的惩罚因子μ＝1，权重因子λ＝2。

（1）当采用文献［2］中的控制方法时，在系统没有受到参数摄动和外界干扰时，对设定曲线有很好的跟踪效果，而在t＞5.0s时，参数a由0.3变到0.6，输出响应已经不能跟踪设定曲线，仿真图如图4所示。

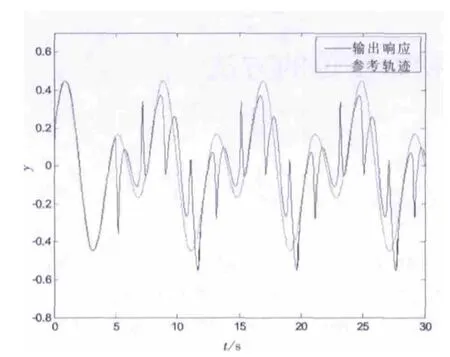
图4 LS-SVM直接逆控制效果

图5 动态补偿的LS-SVM逆控制效果

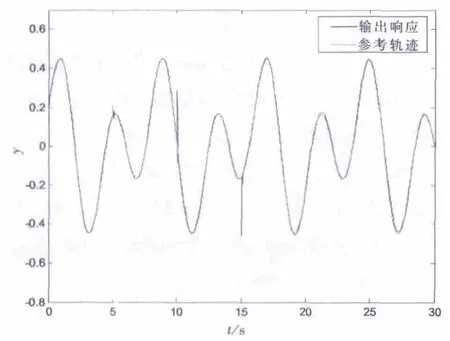
图6 动态补偿的在线LS-SVM逆控制效果

（2）当采用动态补偿的LS-SVM逆控制方法时，在 t＞5.0s时，数a由0.3变到0.6，系统响应曲线只出现微小的抖动；在t＞10.0s时，受到外界强干扰d＝0.2时，系统仍能保持很好的跟踪效果；在t＞15.0s时，发生a＝0.3cos（0.5πt）的时变摄动时，仍具有较好的跟踪效果，仿真图如图5所示。

（3）本文采用基于动态补偿的在线LS-SVM逆控制方法，当出现（2）中同样情形时，控制效果更优于（2）中的控制效果，其仿真图如图6所示。

由仿真图4-6可以看出，本文所提出的方法在参数发生快时变摄动和受到时变强干扰时对设定曲线仍然有理想的跟踪效果，提高了控制器的鲁棒性和系统跟踪精度。

［1］杨志峰，雷虎民，董飞垚.基于LS-SVM的导弹在线误差补偿逆控制［J］.系统工程与电子技术，2010，6（32）：1314-1317.

［2］胡良谋，曹克强，李小刚.基于LS-SVM的非线性系统直接逆模型控制［J］.中国机械工程，2010，13（13）：1553-1556.

［3］刘陆洲，肖 建.基于支持向量机的逆控制及稳定性分析［J］.计算机应用，2008，11（28）：2978-2980.

［4］刘 涵，刘 丁.基于支持向量机的一类混沌系统自适应逆控制［J］.控制理论与应用，2007，5（24）：761-765.

［5］杨 滨，杨晓伟，黄 岚.自适应迭代最小二乘支持向量机回归算法［J］.电子学报，2007，22（10）：1170-1176.

［6］宋夫华，李 平.基于支持向量机α.阶逆系统方法的非线性内模控制［J］.自动化学报，2007，33（7）：778-781.

［7］Suykens J A K，Vandewalle J.Least Squares Support Vector MachineClassifiers［J］.Neural Processing letters，1999，9（3）：293-300.

［8］LI Li-Juan，SU Hong-Ye，CHU Jian.Generalized Predictive Control with Online Least Squares Support Vector Machines［J］.ActaAutomaticSinica.，2007，11（33）：1182-1188.

［9］侯忠生.非参数模型及其自适应控制理论［M］.北京：科学出版社，1999.

［10］侯忠生，许建新.数据驱动控制理论及方法的回顾和展望［J］.自动化学报，2009，35（6）：650-667.