关于谐振子第一积分的研究

丁光涛

1 引言

谐振子是力学和物理学中基本的模型之一,很多理论研究和工程实际应用研究都建立在这个模型之上[1,2].微振动系统是可积系统,然而,有关的问题,例如系统存在多少个不含时的独立积分以及如何导出这些积分,仍是受关注的课题,很多系统的量子化与这些积分(守恒量)有关[3-6].文献[7]用扩展的P-S方法得到了二维非对称谐振子系统分振动的频率比为有理数情况下的第三个独立的积分,但是,对分振动的频率比为无理数情况下是否存在第三个独立的积分问题,未做明确回答.

本文继续研究谐振子系统不含时的独立积分问题,探讨构造这种特殊系统积分的新方法.首先,对一维谐振子提出基本积分的概念,以及与之相关的构造系统其他积分的直接方法.其次,将这种概念和方法推广到二维系统,并给出利用不同自由度的基本积分构造系统其他积分的方法,证明所有的二维谐振子,包括对称的和非对称的两种系统,以及对非对称的系统中分振动的频率比为有理数和无理数两种情况,都存在能量积分之外的第三个独立的与时间无关的积分,并对这些积分进行了分析讨论.最后,将一维和二维系统的结果直接推广到n维谐振子系统,利用上述方法直接构造独立的不含时积分,从而证明这种系统存在2n-1个独立的不含时的第一积分.

2 一维谐振子的基本第一积分

一维谐振子的运动微分方程为[1,2]

方程的两个第一积分为

将t=0时的初始条件I11代人,即可知道I1和I2分别与初位置和初速度直接相关,它们是两个独立的积分.由这两个积分可以直接得出方程(1)的解

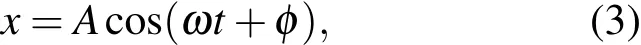
而且利用它们能够构造其他的积分,例如

容易证明,I3是振子能量,直接与振幅A相关

I4与振子初位相φ相关

在上述积分中,I3与时间无关,给出了系统在相空间的轨道,然后直接积分这个一阶微分方程,或是结合另外的与时间相关的积分用代数方法求解,就能确定谐振子的运动规律.

从运动积分还能够直接构造谐振子的Lagrange函数[8],例如,由I3可以构造得到

由I1和I2还可以分别构造得到两个Lagrange函数族

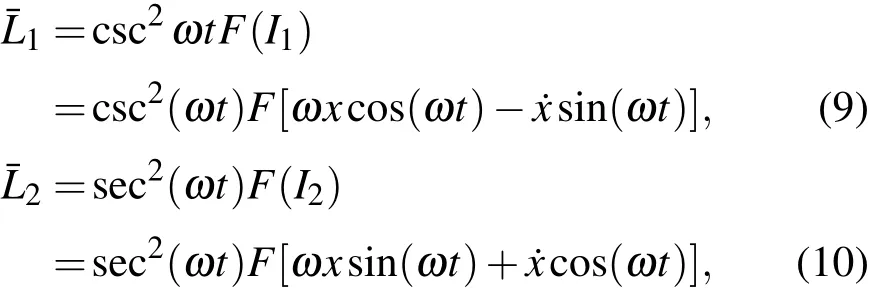
其中函数F应满足条件

因为(2)式中两个积分与初位置和初速度直接相关,既能直接导出谐振子的解,又能构造其他积分,还能构造Lagrange函数和函数族,所以我们将它们称为谐振子的基本积分,这个概念是下面讨论的出发点.在此指出,下面只讨论构造谐振子的积分问题,而不再涉及构造Lagrange函数问题.

3 二维对称谐振子的第一积分

将上述一维情况推广到二维情况.首先讨论对称谐振子,其运动方程为

方程的四个独立的基本积分为

这四个独立的积分的物理意义清楚,利用它们同样能够导出二维谐振子的解,也能利用它们构造二维谐振子其他的积分.例如,与两个分振动对应的能量积分和初位相积分

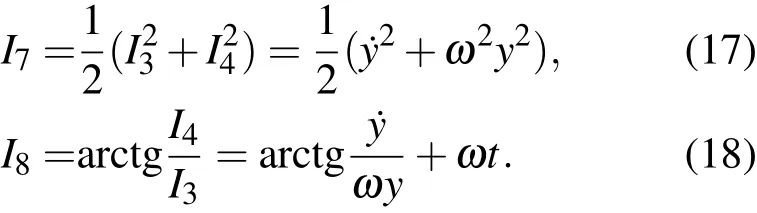
由此还可以得到涉及整个系统的积分,例如,总能量

和(初)位相差

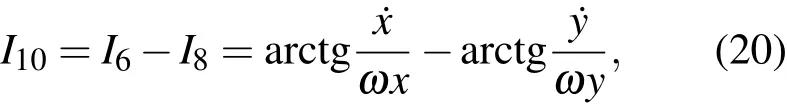
以及其他整个系统的积分,例如,

积分I11与两个分振动的振幅和初位相差相关,I12相当于角动量守恒,对于二维对称谐振子而言,这两个积分也是重要的积分.

由于(13)和(14)式中四个第一积分的任意函数都是新的积分,故二维对称谐振子的积分有任意多个,其中大部分是含时的.但是,在讨论系统运动时,人们往往更重视寻找与时间无关的积分[1,3,7],如(15),(17),(19)—(22)式中的积分,每一个这样的积分都表示系统相点在相空间中一个不随时间而变化的曲面上运动,对2个自由度的系统而言,如果导出3个独立的不含时积分,这些积分在相空间表示不同的固定曲面,它们的交线就是系统相点的轨道,如果再导出一个与时间相关的积分,那么,相点在轨道上的运动规律就可以确定[1,2].上面给出的二维对称谐振子的6个不含时积分并不是彼此独立的,例如,I5,I7和I9,不是彼此独立的;I6,I8和I10也不是彼此独立的.对二维系统而言,最多只能有4个彼此独立的积分,而独立的不含时积分最多只能有3个.二维对称谐振子是简单可积系统,它的四个独立第一积分是容易全部得到的,例如,(13)和(14)式中四个第一积分就是彼此独立的,(15)—-(18)式中四个积分也是彼此独立的,三个独立的不含时积分也容易给出,如(15),(17),(20)式,或(19),(20),(22)式等.总而言之,利用四个基本积分,构造二维对称谐振子的其他积分问题,包括构造独立的不含时积分问题,就完全解决了.

4 二维非对称谐振子的运动积分

讨论二维非对称谐振子,其运动方程为

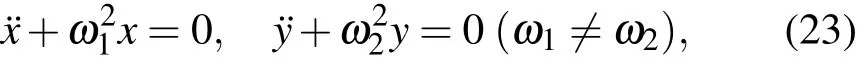
同样可以得到方程的四个基本的运动积分

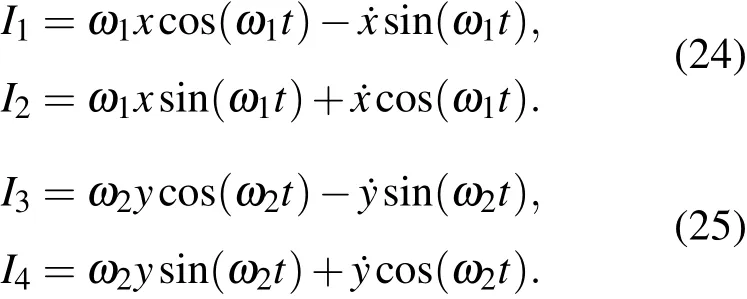
利用这四个积分同样能够导出二维非对称谐振子的解,以及构造二维谐振子其他的积分,例如,与两个分振动对应的能量积分和初位相积分

应当再次指出,二维谐振子运动无论是对称的还是非对称的,都是可积系统,都能得到四个独立的运动积分,如(24)和(25)式中或是(26)—(29)式中的四个积分.

仍存在其他涉及整个系统的积分,如总能量

但是,直接与上面(20)—(22)式对应的积分则不存在了,这是因为ω1/=ω2的缘故.不含时的能量积分I9和I5,I7彼此相关,独立的只有两个.因此,要讨论第三个这样的不含时的独立积分是否存在,如果存在将如何构造的问题[7].

通常认为,第三个不含时的独立积分是否存在的问题与系统的相轨道是否闭合,系统的运动是否为周期运动的问题相关[1-3,7].已经明确的是,当两个自由度的振动频率之比为有理数,即ω1/ω2=p/q,p,q为整数时,二维谐振子运动的相轨道是闭合的,系统运动是周期的,第三个不含时的独立积分存在;然而当振动频率之比为无理数时,二维谐振子运动的相轨道不是闭合的,系统运动是非周期的.第三个不含时的独立积分是否存在呢?有关文献中并没有回答.我们将在上面讨论的基础上,直接从构造运动积分的途径,来研究第三个不含时的独立积分的问题,对振动频率之比为无理数情况给出答案.

不难看出,前面一维振子和二维对称谐振子,从四个基本的含时的运动积分导出不含时的运动积分是通过代数运算消去时间因子得到的.在二维非对称振子情况,振动频率之比为有理数时,除了能量积分外,仍然能够通过有限次的代数运算从四个基本的含时的运动积分中再消去时间因子,得到新的不含时的积分.这里的方法与文献[7]不同,作为实例并为了简化讨论,下面只处理ω1/ω2=2的情况,此时(24)和(25)式可以改写成

由(32)式可导出

从(31)和(33)式消去时间因子,导出新的独立的不含时的积分为

这个积分与文献[7]中的结果一致.

但是,还有一种更简单的方法直接导出另一个独立的不含时的积分

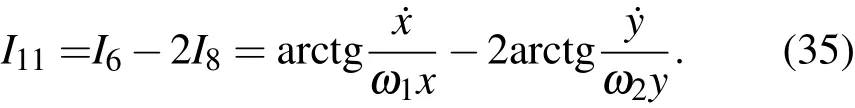
这个积分可以看作(20)式中积分的推广,可以将它变换成代数函数形式

这是一个不同于I10的积分.

当ω1/ω2为无理数时,不能导出类似I10的积分了,但是,能够导出类似I11的积分

这就是第三个不含时的独立积分.然而,由于ω1/ω2为无理数,积分I11与积分I12之间有重要区别,I12不能变换为代数函数形式,积分I11在相空间的曲面是闭合的,而积分I12在相空间的曲面不是闭合的,与其他积分曲面的交线构成不闭合的相轨道,系统的运动是非周期的.应当指出,(37)式形式的积分是一种普遍的形式,并不仅限于ω1/ω2为无理数的情况.ω1/ω2为有理数,包括等于1的情况,都存在这种形式的积分,(20)和(35)式的积分是其特例.

上面给出了从二维谐振子同一个自由度和不同自由度的基本积分构造谐振子系统其他积分的方法.利用这种方法证明了对二维谐振子不论是对称的,还是非对称的,也不论两个振动的频率比是有理数,还是无理数,都可以在能量积分之外构造得到第三个独立的与时间无关的积分.频率比是有理数的系统第三个独立的与时间无关的积分是代数函数,或是可以变换成代数函数形式,三个独立的与时间无关的积分在相空间中曲面的交线是闭合的相轨道,系统的运动是周期的;频率比是无理数的系统第三个独立的与时间无关的积分是超越函数,不能变换成代数函数形式,系统的相轨道不是闭合的,运动不是周期的.这种讨论是纯理论的.谐振子模型是一种理想模型,在实际的物理系统中,频率比是1,是有理数,还是无理数,都只是理想情况.两个自由度间微小的耦合,运动初始条件的细微变化,系统非线性的微弱存在,都会对系统的运动,特别是长期运动产生影响.

5 多维谐振子系统的运动积分

对一维和二维谐振子的积分问题的讨论,得到了如何从同一个自由度振动和不同的自由度振动的基本积分构造其他积分的方法,显然,这种方法容易推广到n维谐振子.设n维谐振子系统的运动微分方程组为

其中n个频率ωi可以相等或不相等;不相等的频率之比,可以为有理数或无理数.对应于每一个自由度的分振动都存在(2)式形式的基本积分

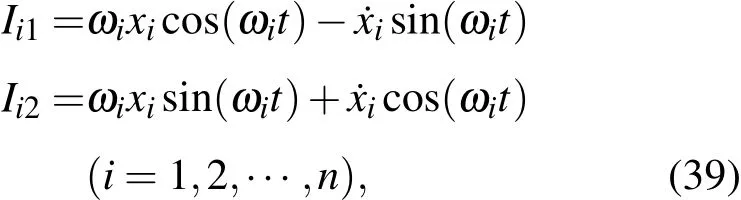
这2n个积分是彼此独立的第一积分.利用它们能够构造对应于振动能量和位相的积分

这2n个积分也是彼此独立的第一积分.(40)式中n个能量积分与时间无关,还可以进一步推导其他的与时间无关的第一积分.对频率相等的分振动,可以得到(20)式形式的积分,它们对应着分振动的初位相差,也可以得到(21)和(22)式形式的积分;对频率不相等的分振动,可以得到(37)式形式的积分,等等.显然,能够导出的不含时的第一积分是相当多的,而我们关心的是能够构造得到多少个独立的不含时的第一积分.

下面用构造法证明对n维的谐振子系统,总能够得到(2n-1)个独立的不含时积分.取第一个分振动为基准,设频率等于ω1的分振动有m个(m≤n),将这m个分振动排在前面,即ω1=ω2=···=ωm,余下的n-m个分振动的频率与ω1不相等,这n-m个分振动的频率之中可能又分为相等或不相等的,但是对下面的证明没有影响.首先,(40)式形式的能量积分有n个,它们是独立的;这些能量积分可以将几个分振动组合起来,甚至整个系统,即全部分振动的能量加起来,得到更多与能量相关的积分,但是,独立的只有n个.其次,m个频率相等的分振动,可以导出m-1个独立的初位相差积分,例如,

余下的n-m个频率与ω1不相等的分振动,可以构成n-m个(37)式形式的不含时积分

(42)和(43)式中共有n-1个独立的不含时积分.总而言之,(40),(42)和(43)式中共有2n-1个独立的不含时积分.这些积分分别与分振动的能量和位相相关,而能量(振幅)和位相是振动现象中具有特征意义的物理量.导出2n-1个独立的不含时积分,就确定了系统代表点在相空间的轨迹,再利用一个含时的第一积分,就可以确定相点沿相轨迹运动的规律.综上所述,n维的谐振子系统是完全可积系统,(39)式中2n个第一积分,或(40)和(41)式中2n个第一积分,都是系统的独立的第一积分;而且通过直接构造得到(40),(42)和(43)式形式的与时间无关的第一积分,证明n维的谐振子系统存在着(2n-1)个独立的不含时的第一积分.

6 结束语

本文研究谐振子的不含时积分问题,给出构造这种积分的新途径,在力学和物理学中,人们往往对这样的运动积分更重视,它们与经典力学中系统相点在相空间的轨道的封闭性和运动的周期性相关,与量子力学中系统的不同量子化模式相关.首先,本文讨论一维谐振子,提出基本积分的概念,以及利用基本积分构造其他积分的方法.其次,将基本积分的概念和构造其他积分的方法推广到二维情况,并解决如何利用不同自由度振动的基本积分构造新的与时间无关的积分的问题,证明了对不同类型的二维谐振子都存在3个独立的不含时的积分.最后,将这种方法推广到n维谐振子系统,利用直接构造法证明n维谐振子总是存在2n-1个独立的不含时积分,并给出这样2n-1个独立的不含时积分的实例,这些积分由基本积分导出并分别与振动能量和位相组合相关.

本文对二维谐振子的积分问题讨论得比较详细,对称的二维谐振子可以构造得到的不含时积分函数形式比较多.对非对称二维谐振子系统而言,两个分频率比是有理数还是无理数,两种情况存在重大区别.频率比是有理数时系统的相轨道闭合,运动是周期的;频率比是无理数时,系统能量积分之外的第三个独立的与时间无关的积分是超越函数,相轨道不能闭合,运动是非周期的.但是,研究结果表明,相轨道是否为闭合的运动是否为周期的,并不能决定第三个独立的与时间无关的积分能否存在,各种类型的二维谐振子系统都存在三个不含时的独立积分.

[1]Goldstein H,Poole C,Salko J 2005 Classical Mechanics(3rd Ed.)(Beijing：Higher Education Press)

[2]Li D M,Chen C M 2006 Classical Mechanics(Beijing：Higher Education Press)(in Chinese)[李德明,陈昌民2006经典力学(北京：高等教育出版社)]

[3]Zeng J Y 2001 Quantum Mechanics(Beijing：Science Press)(in Chinese)[曾谨言2001量子力学(北京：科学出版社)]

[4]Um C I,Yeon K H,George T F 2002 Phys.Rep.362 63

[5]Ling R L,Feng J F 2009 Acta Phys.Sin.58 2164(in Chinese)[凌瑞良,冯金福2009物理学报58 2164]

[6]Hao J H,Huang X Y 1998 Acta Sin.Quant.Opt.4 49(in Chinese)[郝剑红,黄相友1998量子光学学报4 49]

[7]Lou Z M,Mei F X 2012 Acta Phys.Sin.61 110201(in Chinese)[楼智美,梅凤翔2012物理学报61 110201]

[8]Ding G T 2011 J.Dynam.Control.9 102(in Chinese)[丁光涛2011动力学与控制学报9 102]