梯度计算的集合变分方案及其在大气Ekman层湍流系数反演中的应用*

韩月琪 钟中 王云峰 杜华栋

1 引言

由于人类活动主要位于大气边界层中,而且边界层中湍流输运作用对地-气物质能量循环起着至关重要的作用,因此各种时空尺度的大气模式和污染物扩散模式都必须要对大气边界层问题进行足够精确的刻画.大气湍流问题是一个远未解决的自然科学难题,所以大气边界层数值模拟和业务数值预报模式以及许多研究工作对于湍流摩擦这一物理过程均采用了经验参数化的方法,即根据大量试验给出大气湍流系数的某种经验形式[1-3].事实上,湍流系数是一个很难确定的物理参数,它与大气的动力、热力结构密切相关.因此给出大气湍流系数合理的计算方法无论对于发展理论研究还是改进业务数值天气预报、污染物扩散计算都是非常迫切和重要的.

实际上,完全可以把确定边界层湍流系数的方法视为一个反问题,即在知道部分风场观测资料的前提下,根据一定的边界层模型来反演湍流系数.反演方法与技术在目标识别、探地雷达、地球物理遥感、医学成像、无损检测等许多领域得到了不同程度的应用,且其研究与开发的前景广阔[4-15].

本文基于牛顿迭代优化反演方法,将集合计算和变分法结合起来,提出了一种目标函数梯度计算的集合变分方案,实施起来简单、方便,并根据正演模式的线性化情况提出了两种计算流程.这种梯度计算方案也可应用于最速下降法、共轭梯度法、变尺度法、组合法等反演方法.在理论推导工作的基础上,本文利用模拟观测资料对大气边界Ekman层的湍流系数进行了反演试验,并对反演结果进行了讨论分析.为实际应用观测资料反演Ekman层湍流系数提供了理论基础与技术保证.

2 梯度计算的集合变分方案

根据观测资料和物理约束来反演未知参数.首先根据最小二乘原理,建立将未知参数作为控制变量的目标泛函,然后计算目标泛函对于控制变量的梯度,采用优化迭代,使目标泛函达到极小值.

2.1 目标泛函

状态空间表示为S∈RNs,其中Ns表示状态维数,x∈S为状态向量.设正演模式为

其中y是模式输出值;x为模式输入值,除已知值外,在此特指控制变量或待反演参数;M为物理模式.对于(1)式,普遍讲,由x求y就是正演;而由y求x即是反演.利用y的观测资料yobs对未知参量x进行反演,目标泛函取为

其中上标T表示矩阵转置.当泛函J的值越小,表明采用反演值计算的模式输出值与观测值的一致程度越高;同时说明反演得到的参数越准确.反演的最终目的是在反演参数满足物理模式(1)式的条件下,使目标泛函(2)式达到极小值.为了使用物理反演算法,采用优化迭代得到反演参数,需要计算目标泛函对于控制变量的梯度.

2.2 梯度的集合变分计算

为了采用集合变分方案计算目标函数对于控制变量的梯度,这里有一系列的未知参数状态向量用来集合预报,其中NE为集合数.初始未知参数猜值的状态向量表示为 x0,假设初始猜值的误差满足高斯分布[16],NE个未知参数状态向量为其中

将NE+1个未知参数状态向量代入正演模式M进行集合计算,可以得到NE+1个模式输出向量,表示为

未知参数的反演值x可以写成初始猜值x0和订正值之和,订正值属于子空间A[17],

x-x0∈A可以表示为线性组合

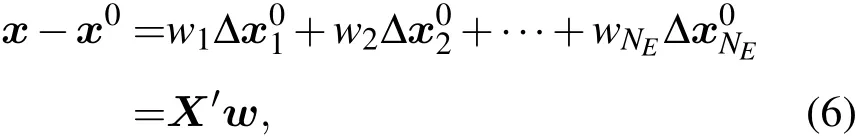
定义新息(innovation)

则

在M可微的情况下,

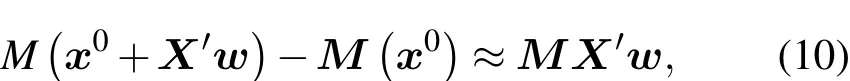
其中M是正演模式M的切线性算子.将(9),(10)式代入(7)式可以得

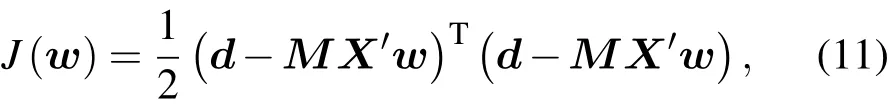
可以求得目标泛函(11)式对控制变量w的梯度

但在(12)式中必须要用到正演模式M的切线性算子M及其伴随模式MT,为了避免使用伴随模式,(12)式变为

采用集合预报结果,可以采用近似计算方法：

这样就避免了使用切线性算子M及其伴随模式MT,从而求得∇wJ.采用优化迭代算法,得到J(w)达到极小时的w代入(6)式,便可得到未知参数的反演值.

3 反演算法迭代格式

在求出目标泛函对于控制变量w的梯度之后,本文选择有限内存拟牛顿优化算法(L-BFGS方法)[18,19],对控制变量w进行迭代,步骤如下：

选择初始未知参数猜值x0=x0⇔w0=0,定义d0=-(∇J)0=-∇wJ(w0);0←k;

1)计算(∇J)k+1=∇wJ(wk+1);

2)令 sk=wk+1-wk,qk=(∇J)k+1-(∇J)k;

3)令ρk=1/qTksk,vk=(I-ρkqksTk);

4)计算

5)令 dk+1=-Hk+1(∇J)k+1;

6)更新wk+1=wk+αkdk,湍流系数xk+1=x0+X′wk+1,其中实数αk使得J(xk+1)最小;

返回第1)步,直到迭代收敛为止.

4 两种计算流程

由(10)式可以看出,在M为线性或非线性非常弱的情况下,MX′在迭代计算过程中变化很小.为了节省计算量,减少集合计算的次数(只需进行一次集合运算),计算流程1如图1所示.

对于M非线性较强的情况,MX′在迭代计算过程中与x值的变化密切相关,MX′的变化会对反演结果产生较大的影响.为了能准确计算随x变化的MX′值,计算流程2如图2所示.

图1 计算流程1

图2 计算流程2

通过对比分析两计算流程可以发现,流程2每次求取梯度都需要进行一次集合计算,这无疑使计算量增加了很多.流程2计算量虽然增加了,但在M非线性较强的情况下,可以较为精确地计算MX′值.

5 计算实例

5.1 正演模式

湍流系数k随时间不变,大气边界层定常状态下的运动方程组为[1]

边界条件为(u,v)|z=0=(0,0);(u,v)|z=H=(uHg,vHg),其中k为湍流系数,u,v为水平风场纬向、经向分量,ug,vg为地转风纬向、经向分量,f为科氏参数,uHg,vHg为边界层顶地转风纬向、经向分量,H为边界层顶高度.在(15)式中,由湍流系数k计算风场u,v是正演,而根据风场求k就是反演.

在已知探空观测风场资料uobs,vobs的条件下,可以对湍流系数k进行反演.地转风场ug,vg可以由水平气压分布计算得到,因此在这地转风作为已知参数.为此,取目标泛函为

为了进行数值计算,首先对方程(15)进行差分离散,在垂直方向将边界层平均分为n+1层,即地面为第0高度,边界层顶为第n+1高度,边界条件给在这两个高度上,显然每层高度为h=H/(n+1).将湍流系数k写在半格点上,其余量都写在整格点上,即ki=k[(i-0.5)h],u(i)=u(ih),其余量以此类推,这样

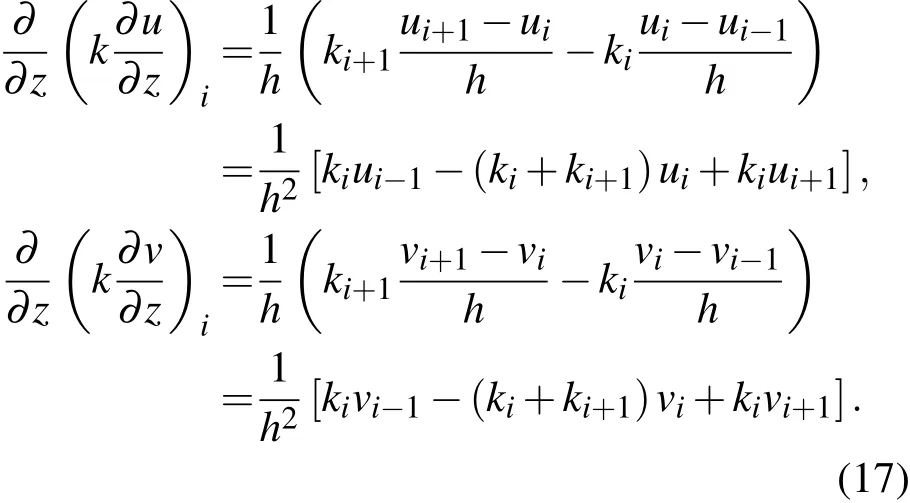
如此代入整理得方程(15)的离散格式.

当 i=2,···,n-1 时,

其中uT=uHg,vT=vHg,为边界层顶地转风纬向、经向分量.记βi=-(ki+ki+1),n×n阶矩阵

则原正演模式(15)式的离散方程写成矩阵形式

这样在给出风速上下边界值和各系数廓线时,原正问题归结为解此2n阶线性方程组.

目标泛函(16)式是一个垂直方向的定积分,采用梯形公式得

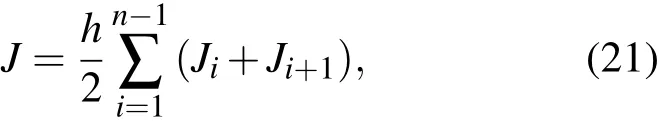
其中

5.2 试验设计

设边界层上界高度H=2000 m,取北纬40°的科氏参数f=0.0000937442 s-1,在垂直方向将边界层平均分为80层.为了对上面的算法进行检验,类似于有关文献选取湍流系数模拟真值(后面都称其为真值)为如下表达式[20]：

kt(z)的单位为m2·s-1,上标t表示真值.地转风随高度线性变化如下：

单位为m·s-1.在这些条件下,把正问题求解Ekman方程(20)式得到的u,v作为风场模拟观测值.根据u,v风场模拟观测资料,做理想数值试验.将湍流系数作为未知参量进行反演,与湍流系数真值(即模拟真值)进行对比,来检验上述方法的可行性及效果.

为了检验初猜值扰动大小及两种计算流程对反演结果的影响,按初猜值扰动大小设计了两组试验：第一组中湍流系数初始猜值扰动较小,初猜值为k(z)=kt(z)+0.1kt(z),集合预报扰动均方差取为0.01 m2·s-1,集合数为100;第二组初始猜值扰动较大,初始猜值为k(z)=8 m2·s-1,集合预报扰动均方差取为0.1 m2·s-1,集合数同样设为100.同时,在这两组试验中分别对两种试验流程进行了试验检验.

5.3 试验结果

图3给出了第一组数值试验中湍流系数的真值、初猜值和反演值的结果,其中图3(a)为流程1的结果,图3(b)为流程2的结果.在这组试验中,初始猜值扰动较小,只是真值的十分之一,即初猜值为k(z)=kt(z)+0.1kt(z).从图3中可以发现,流程2反演结果的精度明显要高于流程1的结果.对于流程1,湍流系数反演结果在800 m以下精度相对较高,800—2000 m的反演值与真实值相比明显存在一定幅度的振荡现象.而对于流程2,可以发现,整个高度上的反演结果都比较接近于真值.

为了更清楚地反映数值试验结果,图4给出了第一组试验中两个流程的反演值与真值之差.从图4中可以发现,在整个高度上流程2的反演精度要明显高于流程1,结论和图3相同.

图5给出了第二组数值试验中湍流系数的真值、初猜值和反演值的结果,其中图5(a)为流程1的结果,图5(b)为流程2的结果.在这组试验中,初始猜值扰动较大,即初猜值为k(z)=8 m2·s-1.从图5中可以发现,流程2反演结果的精度明显要高于流程1的结果,这和第一组试验得到的结论相同.在这组试验中,对于流程1,湍流系数反演结果与真实值相比在整个高度上都明显存在一定的震荡;对于流程2,反演值除了在湍流系数随高度变化拐角处存在一定误差外,其他高度上的反演结果都比较接近于真值,反演精度比较高.

图3 第一组试验中湍流系数的真值、初猜值和反演值(a)流程1;(b)流程2

图4 第一组试验中反演值与真值之差

图6 给出了第二组试验中两个流程的反演值与真值之差,可以发现,在整个高度上,流程2的反演结果精度要明显高于流程1,得到的结论与图5相同.

另外,将图3、图4与图5、图6相比较,可以发现,除了不同的计算流程对反演结果精度有较大影响外,湍流系数初始值的扰动大小对最后的反演结果也有较大的影响.表1给出了采用集合变分方法反演Ekman层湍流系数两组试验中不同计算流程的机器用时(Inter(R)Core(TM)2 Duo CPU T5550,1.83 GHz,1.00 GB的内存)及反演误差均方差.从表1的数据可以看出,在相同计算流程的情况下,初猜值扰动较小情况下的反演误差均方差要小于初猜值扰动较大的情况;在初猜值扰动相同的情况下,流程2反演结果的误差均方差要远小于流程1,但机器用时要远高于流程1.

图5 第二组试验中湍流系数的真值、初猜值和反演值(a)流程1;(b)流程2

图6 第二组试验中反演值与真值之差

综合以上数值试验结果可以发现,提出的集合变分梯度计算方案能够有效减小初猜值中的误差,使反演值向真实值接近,反演结果的精度与初猜值扰动的大小及反演计算流程有关.

表1 集合变分方法反演Ekman层湍流系数的数值结果

6 结论

在进行大气边界Ekman层湍流系数物理反演计算过程中,将集合计算和变分法相结合,提出了目标泛函梯度计算的集合变分方案,避免了根据正演模式推导伴随模式求梯度的繁琐过程,此方法的梯度计算只需要正演模式,使得算法实现变得简单、方便.

采用此方案对大气边界Ekman层的湍流系数进行了反演数值试验.计算结果表明,提出的方案能够有效减小初猜值中的误差,使反演值向真实值考近,避免了根据正演模式推导伴随模式求梯度的繁琐过程,这说明此反演方法中梯度计算的集合变分方案是可行的.同时试验结果表明,湍流系数初猜值的扰动大小及不同的计算流程都会对反演结果产生较大的影响.在相同计算流程的情况下,初猜值扰动较小情况下的反演误差均方差要小于初猜值扰动较大的情况.分析其原因,由反演方法采用的目标函数定义(2)式及集合变分梯度计算方法中集合扰动均方差的选取,此方法实质上是一个极大似然估计方法,因此初猜值扰动小(即误差小),那么估计值(或反演值)的误差均方差就小;反之,则反演值误差均方差就大.另外,在初猜值扰动相同的情况下,考虑MX′随x变化计算方法(即流程2)的反演误差均方差要远小于不考虑随x变化的反演计算方法(即流程1).这主要是因为,大气边界Ekman层模式(即正演模式M)是一个非线性模式,MX′会随x迭代过程的变化而变化,如不考虑MX′的变化,就会将误差转化到最后的反演结果上,从而产生较大的反演误差.

[1]Berger B W,Grisogono B 1998 Bound.Layer Meteorol.87 363

[2]Masson V 2000 Bound.Layer Meteorol.94 357

[3]Grimmond C S B,Oke T R 2002 J.Appl.Meteorol.41 792

[4]Chen J,Kemna A,Hubbard S S 2008 Geophysics 73 247

[5]Sheng Z,Huang S X 2010 Acta Phys.Sin.59 1734(in Chinese)[盛峥,黄思训2010物理学报59 1734]

[6]Zhang Y,Yang X,Gou M J,Shi Q F 2010 Acta Phys.Sin.59 3905(in Chinese)[张宇,杨曦,苟铭江,史庆藩2010物理学报59 3905]

[7]Ye H X,Jin Y Q 2009 Acta Phys.Sin.58 4579(in Chinese)[叶红霞,金亚秋2009物理学报58 4579]

[8]Zhang Y Q,Ge D B 2009 Acta Phys.Sin.58 4573(in Chinese)[张玉强,葛德彪2009物理学报58 4573]

[9]Zuo H Y,Yang J G 2007 Acta Phys.Sin.56 6132(in Chinese)[左浩毅,杨经国2007物理学报56 6132]

[10]Wei B,Ge D B,Wang F 2008 Acta Phys.Sin.57 6290(in Chinese)[魏冰,葛德彪,王飞2008物理学报57 6290]

[11]Huang C J,Liu Y F,Wu Z S,Sun Y Q,Long S M 2009 Acta Phys.Sin.58 2397(in Chinese)[黄朝军,刘亚峰,吴振森,孙彦清,龙姝明2009物理学报58 2397]

[12]Hao N,Zhou B,Chen L M 2006 Acta Phys.Sin.55 1529(in Chinese)[郝楠,周斌,陈立民2006物理学报55 1529]

[13]Shi X M,Xiao M,Fan J K 2009 J.Geophys.52 1140(in Chinese)[师学明,肖敏,范建柯2009地球物理学报52 1140]

[14]Wang J Y 2007 J.Engin.Geophys.4 1(in Chinese)[王家映2007工程地球物理学报4 1]

[15]Kelbert A,Egbert G D,Schultz A 2008 Geophys.J.Inter.173 365

[16]Cohn S E 1997 J.Meteor.Soc.Japan 75 257

[17]Jazwinski A H 1970 Stochastic Processes and Filtering Theory(1st Ed.)(New York：Academic Press)p376

[18]Liu D C,Nocedal J 1989 Math.Programming 45 503

[19]Nocedal J 1980 Math.Comput.35 773

[20]Zhao M 1987 Adv.Atmos.Sci.4 233