基于非均匀螺旋线数据和布雷格曼迭代的快速磁共振成像方法*

2013-09-25方晟吴文川应葵郭华

物理学报 2013年4期

方晟吴文川应葵郭华†

1 引言

缩短数据采集时间一直是磁共振成像发展的核心目标之一.传统快速成像方法通过提高磁场梯度性能加快k空间数据采集速度.然而,受制于生理因素和硬件制约,这类方法加速效果已经接近极限.而近年诞生的压缩感知成像理论,提供了通过欠采样缩短数据采集时间的新途径.压缩感知成像理论指出：如果欠采样导致混迭伪影是空间非连贯的,通过采用合适的非线性重建方法,可以在抑制混迭伪影的同时,完整重建图像信息[1-3].

非均匀螺旋线序列便是一种符合压缩感知成像理论关于混迭伪影的要求的数据采集方法[4].非均匀螺旋线序列在k空间中心附近进行过采样,在k空间周围进行正常采样[5].这使得欠采样情况下,非均匀螺旋线序列的混迭伪影在空间分布呈现出近似不连贯的分布,不会严重破坏图像结构信息[6].同时非均匀螺旋线序列本身便是一种数据采集时间短的超快速数据采集方法[5],在心脏成像、灌注成像等方面已获得应用[6-8],并有望在磁共振弹性成像[9,10]等新领域获得进一步的应用.所以,非均匀螺旋线序列非常适合作为包括压缩感知成像在内的快速磁共振成像的数据采集手段.

实现压缩感知成像的另一个必备条件是能够去除欠采样所引起混迭伪影的非线性图像重建算法.目前在磁共振成像领域上应用较多的非线性重建方法主要有小波域稀疏性约束重建方法[3]和全变分重建方法[11].其中全变分方法在去除噪声和混迭伪影方面获得了一定的成功.然而,全变分方法在抑制欠采样混迭伪影的同时,会造成图像细节结构的丢失[12,13].

为了解决这一问题,本文结合非均匀螺旋线磁共振成像序列和布雷格曼迭代[14]重建,提出一种新的快速磁共振成像方法,并通过数值模拟实验和在体磁共振成像进行了实验验证.实验结果表明,布雷格曼迭代能有效消除混迭伪影和吉布斯振铃伪影,并保持准确的图像结构信息,这对于建立基于非均匀螺旋线的快速磁共振成像方法具有重要推动作用.

2 非均匀螺旋线磁共振成像

2.1 非均匀螺旋线数据采集序列设计

非均匀螺旋线磁共振数据采集序列可以灵活控制k空间的数据采集密度,改变欠采样引起混迭伪影的形态,并针对性地获取实时扫描信息.其k空间轨迹方程为[5]

其中,k(τ)是螺旋线轨迹在k空间的位置;τ是关于时间的方程,决定了螺旋线轨迹的形状;n是螺旋线的匝数;λ是由视野范围FOV和成像矩阵大小决定的常数,λ=N/(2×FOV).

与大多数核磁共振序列一样,非均匀螺旋线序列在磁场梯度爬升过程中会受到最大磁场梯度爬升率的限制;随后当梯度达到硬件允许的最大幅度后,限制条件变为硬件允许的最大磁场梯度幅度.针对这两种不同的边界条件,将(1)式中的τ(t)描述如下：

其中,γ是磁化率;sm和gm分别是最大磁场梯度爬升率和磁场幅度;Ts2α是边界条件由最大磁场梯度爬升率转变为最大磁场梯度幅度的时刻;Tes是边界条件持续为最大磁场梯度爬升率的时间;Tea是非均匀螺旋线序列的结束时刻(起始时刻为t=0).

α是控制采样密度变化的常数(α≥1).α=1对应于均匀螺旋线采样轨迹,整个k空间采样率等于奈奎斯特采样率.欠采样时,混迭伪影形态是连贯的.α＞1时,k空间中心采样率高于奈奎斯特采样率.α越大,k空间中心采样密度越大,欠采样情况下,混迭伪影空间分布连贯性越低,越接近噪声,越有利于运用非线性重建算法去除混迭伪影.

然而,增大α会造成采集时间的增加,所以,非均匀螺旋线需要在缩短采集时间和降低混迭伪影的空间连贯性之间进行均衡取舍.通过实验比对,本文中设计和编写了α=3的非均匀螺旋线数据采集序列,用于在体成像实验数据的采集.

2.2 非均匀螺旋线磁共振成像的重建

非均匀螺旋线磁共振成像可以通过以下的线性方程表示：

其中,s(k)是所采集的k空间信号,ρ(r)是待重建的磁共振图像;k是k空间的位置向量,二维情况下,k=[kx,ky],kx=Re(k(τ)),ky=Im(k(τ));r 是空间向量r=[rx,ry].离散化后,方程(3)可以表示成

其中,s是所采集的k空间信号向量,ρ是待重建的磁共振图像向量;E是由非均匀螺旋线采样轨迹决定的图像编码采样矩阵,具体形式为

其中N为图像矩阵一行的像素数,M为采样数据总数,km是离散化后非均匀螺旋线轨迹上的离散采样点位置向量,rn是离散化后的空间位置向量.图像重建过程便是对(4)式进行矩阵求逆的过程,经典的线性方法包括非直角坐标傅里叶变换[15]和网格插值法[16].但在欠采样条件下,这些线性重建方法无法消除混迭伪影.

3 压缩感知成像框架下的非线性重建

压缩感知成像理论提供了欠采样条件下,利用非线性方法完整重建图像信号的理论框架.根据压缩感知成像理论[2],对于长度为N2的磁共振向量信号ρ,假设经过线性变换x=Ψρ后,可以得到非零值个数为K稀疏信号x.此时,如果采样矩阵E同时满足约束等距性准则：

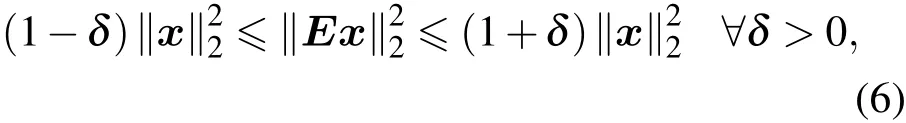
则总共只需采集M=O(Klog(N2/K))·N2个数据,即可以完整重建出信号.在当前实用磁共振采样轨迹中,非均匀螺旋线数据采集轨迹正是与约束等距性条件符合最好的数据采集方式之一[3].

压缩感知成像的重建可以通过求解下述优化问题来实现：

其中J(·)是提升解的稀疏性的非线性泛函;λ是正则化因子.对于目前应用较多的全变分重建方法而言,Ψ 为差分算子矩阵 ∇,J(·)= ‖·‖1为 1-范数,其表达式为

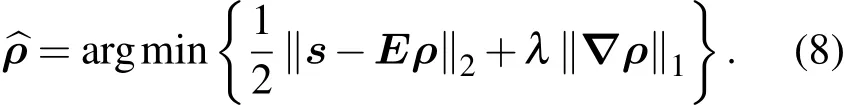
4 基于布雷格曼迭代的重建方法

布雷格曼迭代是在全变分的基础上,通过多次迭代求解全变分泛函J(·)的布雷格曼距离来减小图像结构损失的问题,其表达式为

(9)式有两个重要的性质：首先,在(9)式的迭代过程中,‖s-Eρ‖2单调递减,直至为 0.其次,在 (9)式的迭代求解中,只要满足 ‖s-Eρk‖2＞‖s-Eρtrue‖2,ρ 单调地趋近真实解 ρtrue.因此,布雷格曼方法具有稳定的收敛性;并且通过选择合适的迭代次数,即可以获得混迭伪影得到充分抑制,并且图像结构信息保存较完好的求解结果.

然而,由于J(·)为非线性泛函,qk-1的计算较为复杂.为了简化计算,我们结合(9)式的特点对(10)式进行变换.

当(9)式收敛到稳定最优解时,有

展开可得

同时,收敛到稳定最优解时,有ρk=ρk-1,代入(13)式可得：

即

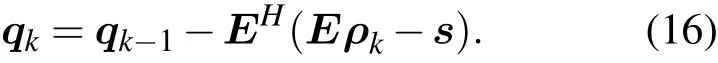
根据(16)式便可以只通过矩阵-向量运算,通过迭代的方法计算出qk-1,避免了计算带来复杂度.因此,(9)式可以通过如下迭代过程求解.

初始值：u0=0,∂J(u0)=0.

对于第k次迭代,有

5 实验系统

为了验证所建立的快速成像方法,分别进行了水模成像实验和在体成像实验,并比较了线性重建、全变分重建和布雷格曼迭代重建三种方法的重建结果.

水模成像实验和在体成像实验均在Philips公司的3 T磁共振扫描仪上进行,采用所编写的自旋回波非均匀螺旋线序列采集数据,具体参数如下：α=3,翻转角度为90°,回波时间TE=20 ms,重复时间TR=500 ms,成像视野220 mm×220 mm,图像采集矩阵大小为256×256.信号采集前有实行高阶匀场.所编写序列的梯度时序波形如图1(a)所示,其对应k空间轨迹如图1(b)所示.

水模成像实验和在体成像实验均首先进行全采样,验证所设计序列的可行性,并同时以全采样数据的重建结果作为比较评价算法的金标准;然后再进行欠采样,仅采集1/3的数据,比较不同方法的重建效果.

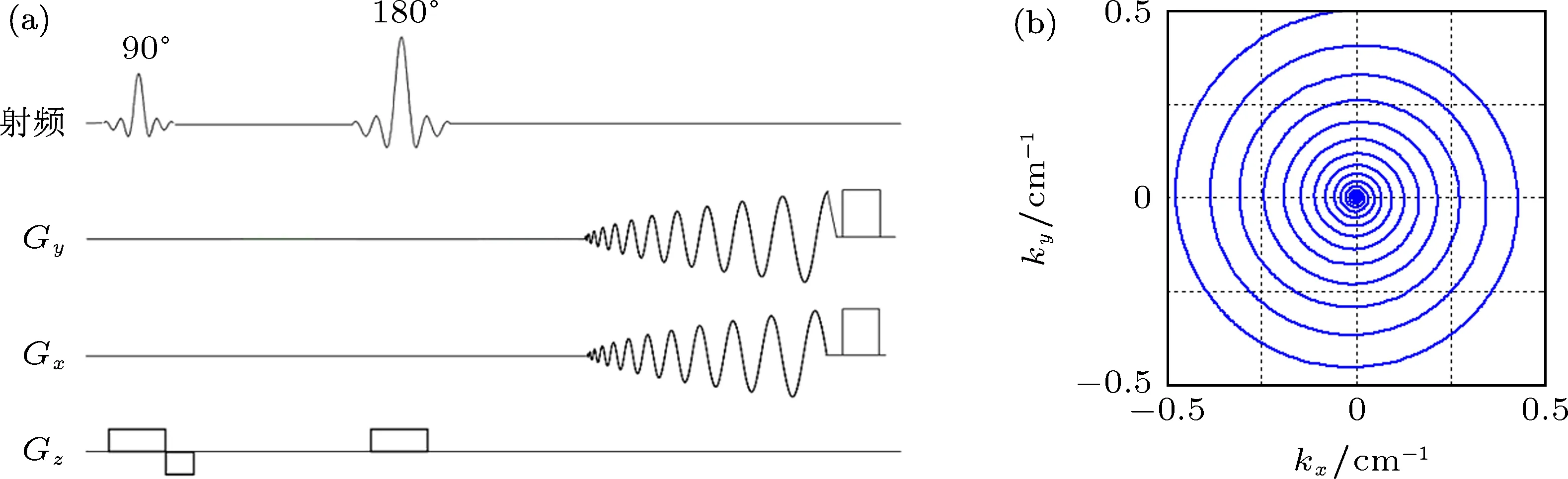
图1 所编写非均匀螺旋线序列的波形与轨迹 (a)梯度波形图;(b)k空间轨迹

6 实验结果分析

图2显示水模成像实验结果.如图2(a)所示,全采样情况下,所设计的非均匀螺旋线序列的成像结果具有较高的信噪比与分辨率,通过高阶匀场,偏共振引起的模糊效应也限制在最低.在欠采样情况下(加速倍数=3),标准线性重建结果出现了混迭伪影.然而这些混迭伪影在空间中分布均匀,并且强度较低,对图像的真实结构信息破坏较少(图2(b)),达到了通过非均匀螺旋线轨迹降低混迭伪影空间连贯性的设计目标.

图2 水模成像实验结果 (a)全采样水模图像;(b)欠采样数据的线性方法重建结果;(c)欠采样数据的全变分方法重建结果;(d)欠采样数据的布雷格曼迭代重建结果

全变分重建结果虽然整体上伪影水平要低于线性重建结果,但是在水模下方的残余混迭伪影依然存在(图2(c)中黑色箭头所指).同时,全变分重建方法还导致了水模中细节结构的模糊(图2(c)中白色箭头所指).而布雷格曼迭代则有效减弱残余混迭伪影的空间强度(图2(d)中黑色箭头所指).并且,布雷格曼重建结果的细节结构清晰(图2(d)中黑色箭头所指).与其他两种重建方法相比,布雷格曼迭代重建结果与全采样水模图像(图2(a))最为符合.

图3显示在体成像实验结果.如图3(a)所示,全采样情况下,所采集的头部图像结构清晰,信噪比较高,并且没有明显的偏共振引起的模糊问题,具有较好的成像质量.在欠采样情况下(加速倍数=3),标准线性重建结果出现了呈振铃状的混迭伪影(图3(b)).然而,由于强度较低,混迭伪影并没有掩盖图像的真实结构信息,对图像的诊断信息破坏较少.

图3 在体成像实验结果 (a)全采样图像;(b)欠采样数据的线性方法重建结果;(c)欠采样数据的全变分方法重建结果;(d)欠采样数据的布雷格曼迭代重建结果

全变分重建方法基本上去除了混迭伪影,然而,全变分重建方法同时也带来了细节结构处图像分辨率的下降问题,出现了一定的模糊效应(图3(c)中箭头所指).布雷格曼迭代则在去除混迭伪影的同时,保持了图像的分辨率,具有清晰锐利的细节结构(图3(d)中箭头所指),和参考图像(图3(a))非常接近.

表1给出了三种重建算法的均方根误差(以全采样图像为金标准).无论是水模成像实验还是在体成像实验,线性重建方法由于混迭伪影的影响,均方根误差误差最大.由于能够有效去除伪影,全变分重建方法的均方根误差小于线性重建方法.而布雷格曼迭代同时解决了线性重建方法的混迭伪影问题和全变分方法的细节结构模糊问题,其均方根误差最小.

表1 三种重建算法的均方根误差比较

7 结论

本文基于压缩感知成像理论,将非均匀螺旋线成像序列和布雷格曼迭代重建方法结合起来,提出了一种新的快速磁共振成像方法,并通过磁共振水模成像实验和在体成像实验对该方法进行了验证.实验结果表明：所提出快速成像方法能够在只采集1/3数据的情况下,有效去除混迭伪影并保持精细的图像细节信息,获得与全采样图像符合良好的成像结果,从而保证了图像质量.该方法显著缩短了磁共振的成像时间,可以解决磁共振成像某些时间分辨率要求高的医学成像应用中的瓶颈问题,有望在心血管成像、脑功能成像和灌注成像等方面中获得进一步的应用.

[1]Cand`es E J,Romberg J,Tao T 2006 IEEE Tran.Inform.Theory 52 489

[2]Donoho D L 2006 IEEE Tran.Inform.Theory 52 1289

[3]Lustig M,Donoho D,Pauly J M 2007 Magn Reson.Med.58 1182

[4]Lustig M,Donoho D L,Santos J M,Pauly J M 2008 IEEE Signal Proc.Mag.25 72

[5]Kim D,Adalsteinsson E,Spielman D M 2003 Magnet.Reson.Med.50 214

[6]Tsai C M,Nishimura D G 2000 Magnet.Reson.Med.43 452

[7]LeeJH,HargreavesBA,HuBS,NishimuraDG2003Magnet.Reson.Med.50 1276

[8]Lu G,Liu M L,Li L Y,Ye C H 2002 Chin.Phys.Lett.19 1385

[9]Bensamoun S F,Glaser K J,Ringleb S I,Chen Q,Ehman R L,An K N 2008 J.Magn.Reson.Imaging.27 1083

[10]Wang H Z,Xu L F,Yu J,Huang Q M,Wang X Y,Lu L 2010 Acta Phys.Sin.59 7463(in Chinese)[汪红志,许凌峰,俞捷,黄清明,王晓琰,陆伦2010物理学报59 7463]

[11]Rudin L,Osher S,Fatemi E 1992 Physica D 60 259

[12]Chan T,Esedoglu S,Park F,Yip A 2006 Mathematical Models of Computer Vision：the Handbook(Boston,MA：Springer)p176