Turbo码并行无冲突交织器设计﹡

丘选锋， 赵宏宇

（西南交通大学信息编码与传输省重点实验室，四川 成都 610031）

0 引言

1993年出现的Turbo码，以接近香农限的性能证明了信道编码定理的正确性[1]。采用迭代译码是Turbo码优异性能的重要原因。但迭代译码的时延较大。并行译码方案则能够显著地降低时延，但交织器的随机置换可能引起存储器的地址争用问题[2]。对此，提出了并行交织器。现有的并行交织器主要有：二次置换多项式交织器(QPP)[3]，行列 S交织器[4-5]。3GPP则采用在短交织块时有较好性能的QPP交织器[6]。但QPP交织器的系数选择有严格的限制[3]。行列S型交织器则是通过行和列的S交织产生的，对整个交织器，其S值不固定且偏小。对此，文中提出了一种新的并行交织器设计方案，S值是基于整个交织长度设定的。

1 无冲突限制和S型交织器

1.1 并行无冲突限制

设 X={x1,x2,…,xN}为交织器的输入比特序列，xi∈{0,1}，1≤i≤N。经过交织器置换后输出Y={y1,y2,…,yN}, yi∈{0,1}, 1≤j≤N。Y 包含了 X 的所有元素，但排列顺序不同。X与Y之间存在一一对应关系。定义集合ZN={1,2,…,N}，则可用一个下标映射函数π()i来定义交织器π()i：,ij→ ,ij∈ZN。

考虑交织器π(),i并行度为M，分块长W。并行译码时，M个外信息被要求同时写入存储阵列中，定义函数 ()Mi表示存储阵列中存储器的位置， ()Si表示存储器中的位置，则π(i)=(M(i), S(i)) →{1,2,…,M}×{1,2,…,W}具有以下含义：第i个外信息被写入到存储阵列中第 ()Mi个存储器中 S(i)的位置上，并行无冲突表现为对 ()Mi的限制；

第 j个时序，写入存储阵列中的 K个外信息K = j, j + W ,… , j + ( M - 1)W 若满足：

则存储器争用问题可避免。

1.2 S型交织器

设π(i)表示ZN上的一个交织函数，若π(i)满足：

对 任 意 的 i,j∈ZN且0＜|i - j |≤ S ， 有|π(i) - π (j) |≥ S[7]。则 π(i)为 S型交织器。参数 S称为延展因子。对比均匀交织器，由于S参数约束的引入，S型交织器获得了更好的性能。S值越大，性能越好， S值上限近似为[8]。

2 并行S型交织器设计

2.1 生成算法

长度为 N的交织器π(i)，分 M 块，每块长为W=N/M。首先生成一个M×W的矩阵，矩阵的每列元素均为{1,2,…,M}的随机排列，表示同一时刻信息映射到存储阵列中的不同存储器位置。而存储器中的具体位置用随机方法产生。选择 S ＜N/2, 设NB=2N表示对序列 St(1), St(2),…, St(W)进行循环左移的最大次数，NR=N表示生成数组M[N]和随机序列St(W)的最大次数。具体生成算法如下：

1)初始化变量Nr=0,Nb=0。

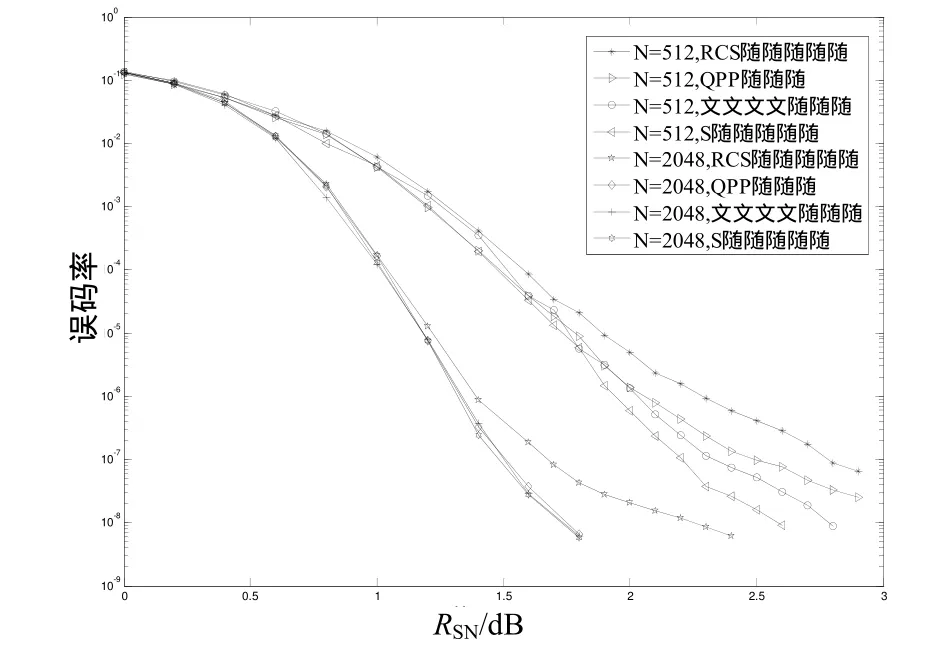
2) Nr=Nr+1，如果Nr=NR，令S=S-1，返回1)；如果Nr

3)生成 M 组随机排列，第 t组 St的元素为{(t-1)×W+1,(t-1)×W+2,…,(t-1)×W+W}的随机排列，初始化nt=1，St[nt]表示第t组随机排列St中的第nt个元素，t={1,2,…,M}。

4)当 i =1，在产生最终交织映射地址 π[1]前，判断 M[1]的值，假如 M[1]=t，t∈{1,2,…,M}，则令π[1]= St[nt]，nt=nt+1；当i >1时，判断M[i]的值，假如 M[i]=t，t∈{1,2,…,M}，则令 π[i]= St[nt]，判断 π[i]是否满足以下条件：

若满足，令i=i+1，nt=nt+1；若不满足，则交换St[nt]和 St[k]，k>nt，若所有的 k=nt+1,nt+2,…,W 都不满足上述条件，则转到5)。

5) Nb= Nb+1；如果Nb= NB，令Nb=0，返回步骤2)；如果Nb

①t[1]～t[W-nt+1]= St[nt]～ St[W];

②t[W-nt+2]～t[W]= St[1]～ St[nt-1];

③St[1]～ St[W]=t[1]～t[W];

且令 i=1，n1～nW=1，返回步骤 4)。

6)重复以上步骤，直到N个交织输出都获得。

2.2 性能验证

在信噪比较大时，误码率由最小重量码字决定。因此可用自由距离来估计和比较不同交织器的性能。在计算不同交织块长的turbo码自由距离时， 采用3GPP标准turbo码，码率为1/3。对每个交织块长，各生成100个行列S随机交织器，S随机交织器和文中建议的交织器。通过约束字码算法[9]计算使用每一个交织所生成的turbo码自由距离，然后求出3种类型交织器的平均自由距离和100个交织器中的最大自由距离。结果列在表1中。从表1中可以看到，使用S型交织器的turbo码字具有较大的自由距离，其次是采用文中方案交织器的turbo码。而采用行列S型交织器的turbo码的自由距离最小。这是因为它的S值偏小。并行度为4时，从表中可以看到文中给出的交织器S值接近 /2N 。

表1 交织器和相应的turbo码自由距离

3 仿真结果及分析

仿真使用生成多项式为(1,13/15)octal的8状态编码器，码率1/3；采用BPSK调制和高斯信道。译码用Max-Log-Map算法，迭代次数为4。仿真对比采用S型、行列S型、QPP和文中方案交织器的turbo码译码性能。仿真结果如图1和图2所示。仿真中使用的3种交织器都是从100个相同类型交织器中选出的具有最大自由距离的交织器。从图 1和图 2可以看到S随机交织器性能最佳，但它不具备并行特征。其次就是文中建议的交织器，而最佳Ω'参数的QPP和行列S随机交织器性能则相对偏差。

图1 误码率（M=4）

图2 误码率（M=8）

4 结语

S随机交织器是一种性能优异的交织器，但它不具备无冲突特性。而把S型交织设计成具有无冲突的特性是一种相对较好和灵活的路线。文中设计方案延续了以往的并行S随机交织器设计方法并且针对现有的并行S随机交织器S参数值较小的缺点，提出了一种新的并行S随机交织器算法。由于S参数的改进，使用文中交织器的turbo码有较大自由距离和较好的误码率并且能够明显地降低译码时延。

[1] 孙丽楠,王学东.Turbo乘积码快速编码 FPGA实现[J].信息安全与通信保密,2007(04):44-46.

[2] 黄卉,王辉.高速并行 Turbo译码中的交织器技术研究[J].通信技术,2008,41(06):83-85.

[3] RYU J,TAKESHITA O Y.On Quadratic Inverses for Quadratic Permutation Polynomials over Integer Rings[J]. IEEE Trans. Inf. Theory, 2006, 52(03):1255-1257.

[4] GAZI O,YILMAZ O.Collision Free Row Column S-random Interleaver[J]. IEEE Commun.lett., 2009,13 (04):257-259.

[5] 史尧,李博.Turbo码并行译码中无冲突交织设计方案[J].通信技术,2010,43(08):137-139.

[6] European Telecommunications Standards Institute 2013. LTE; Evolved Universal Terrestrial Radio Access (E-UTRA); Multiplexing and channel coding(3GPP TS 36.212 version 10.6.0 Release 10)[S]. ETSI TS 136 212 v10.7.0(2013-02), Sophia Antipolis Cedex - FRANCE: ETSI 3rd Generation Partnership Project (3GPP), 2013:11-16.

[7] 郭璐,薛敏彪,黄莺,等.Turbo码中交织器的综合性能分析与设计[J].信息安全与保密,2006(09):72-74.

[8] DIVSALAR D,POLLARA F.Turbo Codes for PCS Applications[C]//IEEE Int. Conf. on Commun. (ICC’95).Seattle: IEEE Conference Publications, 1995:54-59.

[9] GARELLO R, PIERLEONI P,BENEDETTO S. Computing the Free Distance of Turbo Codes and Serially Concatenated Codes with Interleavers: Algorithms and Application[J]. IEEE.J.Select. Areas Commun.,2001,19(05):800-812.