声速测量实验中声压幅度极值的研究

汤 纯,苏建新

(1.同济大学物理科学与工程学院,上海 200092;2.汕头大学物理系,广东 汕头 515063)

0 引言

利用超声换能器形成驻波测量声速的方法,由于其测量简单、图像清晰而被用来测量空气中的声速或测量液体如水或油的声速,并被搬进大学物理实验教学中[1-6].然而长久以来,在许多教科书中[1-2],将两个换能器之间声压幅度随空间的变化规律与施加到接收换能器声压幅度随两换能器之间的距离变化规律混为一谈.陈洁等人[7]以滞粘媒质下的纳维-斯托克司方程为基础导出接收换能器上声压幅度与两超声换能器之间的距离变换规律.从理论上澄清了一些容易被误解的概念.然而,依文献[7]的计算,空气粘滞和弛豫现象引发的吸声系数较小,不足以解释实验中施加到接收换能器声压幅度的极大值和极小值随两换能器之间距离增加而显著下降的实验现象.针对上述问题,作者在本文做了较详细的研究.

1 基本理论

声速测量实验装置如图1所示,在声源的激励下两换能器之间的空气元在平衡位置附近做振动,施加到接收换能器上的声压幅度为[7]

式中υ是发射换能器表面的振动速度幅度(假设为恒定),ρ是空气密度,c是空气中声波的传播速度,k称为波数,是复数,可表示成k=-α j,α为等效吸收系数,l为两换能器之间的距离.

图1 实验装置原理图

当k是一个实数时,sin(kl)极小值为零,这时p达到无限大,但因α的存在,使得sin(kl)不会达到零.随着两换能器之间的距离变化,sin(kl)出现一系列极小值和极大值,对应施加到接收换能器上的声压幅度p达到极大值和极小值.

在空气中,声波的吸声由三部分组成:即切变粘滞引起的吸收,容变粘滞引起的吸收及分子弛豫引起的吸收.前两类吸声系数与频率的平方成正比,而分子弛豫引起的吸收在频率较低时,仍与频率平方成正比.通常吸声系数随频率的变化比平方律慢一些.C.M.Harris给出了摄氏二十度下吸声系数随频率、湿度的变化关系[8],对于10 KHz,相对湿度35%的条件下α≈0.002 m-1,假如α是按频率平方增加,那么40 KHz时,α≈0.32 m-1.由公式(1)得α≈0.32 m-1条件下,声压幅度与距离的关系,见图2.

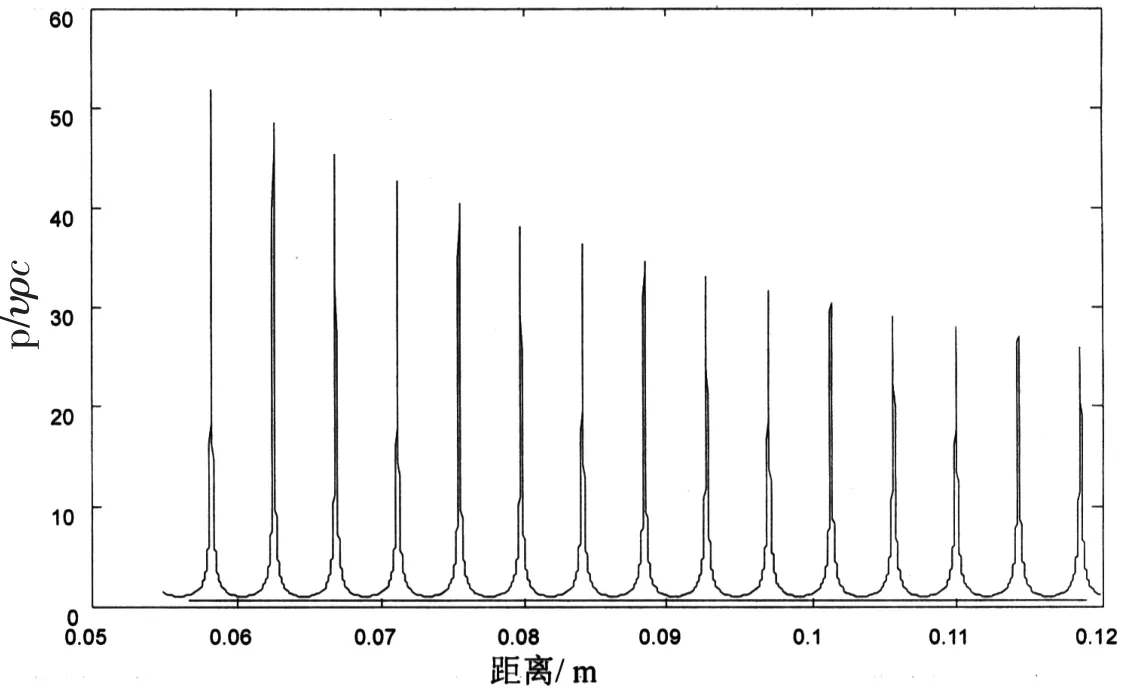
图2 声压幅度随距离变化的理论值α=0.32 m-1

观察上图曲线,得出如下结果:1)声压幅度的极大值,随距离的增加而衰减,这和实验定性相符合,但定量差别较大.2)声压幅度的极小值几乎不变,但实验显示极小值随距离的增加也会明显下降.3)图2横坐标是大部分教课书建议的距离范围,理论计算近处的极小值远小于远处的极大值,这也和实验差别很大.

因此单用前面的普通声吸收机理,不足以解释实验过程中声压幅度随距离的变化规律,本文认为一个比较合理的解释是衍射效应在起作用.

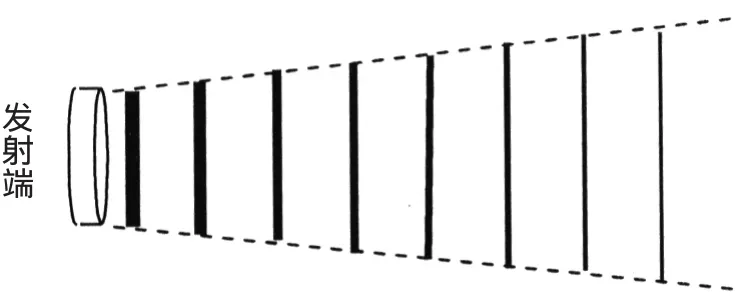
图3 换能器发射的声波随距离的增加而扩散开

实验中发射、接收换能器的工作频率大约是40 KHz.对于空气,声波波长大约是0.86 cm,而换能器的直径大约是2.4 cm,这样会有明显的衍射效应.

如果以l=8 cm为例,可算得爱丽斑半径[9],约为R=0.61Xl=3.5 cm,它大约

为换能器半径的3倍.根据爱丽斑上能量分布函数关系[8],可用下列公式估算一下因衍射带来的声压衰减.

式中J1(x)是一阶Bessel函数(J1(x)的第一个根x=3.83).即从发射换能器处发射的声波传过8 cm,中心处半径为1.2 cm的区域(即换能器的区域)的平均声压已经衰减到原有的0.64倍.如果没有衍射仅考虑粘滞和弛豫要达到这样的衰减程度对应有e-αl≈0.64,即α≈0.55 m-1,这个值比C.M.Harris最大值还要大一个数量级(随着距离的变化该值会有一点变化).因此理论计算应当把衍射效应产生的等效α连同粘滞吸声和分子弛豫吸声一同考虑到公式(1)去.

2 实验

由于两个换能器之间的实际有效距离l和从标尺上读得的距离l′有一点差别,把l换成l=δl+l′,这里δl是常数.声压是要通过示波器电压显示出,把声压p和电压U写成p=AU,A是常数.把(1)代入,通过示波器上读到的峰峰值随距离的变化为:

本文实验选用的距离区段是通常实验教材建议的范围(约5 cm到15 cm)内,本文以实验测得的第一个极大值作为参照点定出常数δl≈0.001 9 m-1和 2υρc/A≈0.63 V.选择的距离点都尽可能选在声压幅度的极值点附近.图4画出电压峰峰值随距离l′变化的理论值("●"表示)和实验值("+"表示)发,结果显示两者非常一致.

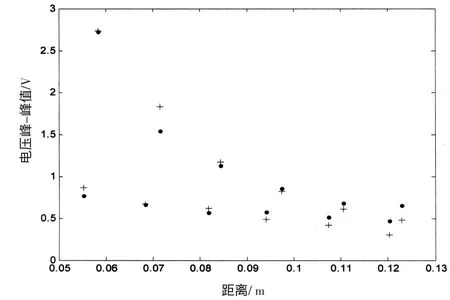
图4 声压幅度随距离变化"●"理论值,"+"实验值

3 结论及讨论

发射换能器与接收换能器之间声压场是个近似的驻波场,施加到接收换能器上声压幅度随两换能器之间的距离l按1/sin(kl)变化.它的极大值和极小值随两换能器之间的距离的增大而显著衰减的现象主要是由衍射效应引起的.这种效应还会对声压幅度的极大值和极小值的分布带来影响,它们已不再严格按照等间距分布了,关于这一点我们将会做出进一步的研究.

[1]李平.大学物理实验[M].高等教育出版社,2003:110-116.

[2]吴平.大学物理实验教程[M].机械工业出版社,2007:85-89.

[3]贾玉润,王公治,凌佩玲.大学物理实验[M].复旦大学出版社,1987:133-136.

[4]陆廷济,费定曜,胡德敬,等.大学物理实验教材[M].同济大学出版社,2000:167-170.

[5]黄耀清,王闳.大学物理实验[M].机械工业出版社,2009:46-54.

[6]黄义清,李斌,周有平.大学物理实验教程[M].电子工业出版社,2012:52-55.

[7]陈洁,苏建新.声速测量实验有关问题研究[J].物理实验,2008,28(6):31-33.

[8]杜功焕,朱哲民,龚秀芬.声学基础[M].上海科学技术出版社,1981:144-211.

[9]朱峰.大学物理[M].清华大学出版社,2008:268-269.