副反应和副反应系数在酸碱滴定误差公式推导中的应用
2013-09-23王园朝包海峰
王园朝 包海峰
(杭州师范大学材料与化学化工学院 浙江杭州 310036)
副反应和副反应系数在酸碱滴定误差公式推导中的应用
王园朝 包海峰
(杭州师范大学材料与化学化工学院 浙江杭州 310036)
摘要通过引入副反应和副反应系数的概念,借助林邦公式的表达形式,讨论了强碱滴定一元弱酸、混合弱酸和多元弱酸滴定误差公式的推导方法,并以实际例题证实所推公式的正确性。
关键词酸碱滴定法 误差公式 林邦公式 副反应推导
误差是分析化学教学中的重点内容,在滴定分析中具有重要的理论价值和实际意义。我们曾按照中心教学法的思想提出了以误差为主线的包含整个分析化学主要知识点的树结构图[1],能较好地反映误差与各知识点间的联系。在分析化学教材中,酸碱滴定法位于四大滴定之首,因此讲清楚酸碱滴定法中的滴定误差概念和公式对讲授其他滴定法至关重要。为了便于教学和清楚地说明影响误差的因素,许多文献[2-6]对四大滴定中滴定误差公式的计算式进行了大量有益的讨论,利用林邦公式统一四大滴定中的误差公式已成为大多数同行的共识,但目前不少教材[7-8]仍然主要以下式来表达强酸滴定弱碱的滴定误差计算式。
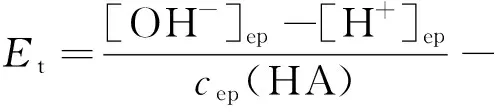
有些教材虽然给出了以林邦公式形式表达的滴定误差计算式,却没有详细的推导过程;而且不同教材、参考书和文献中给出的以林邦公式表达的酸碱滴定误差计算式也不一致,这些给教学带来了一定的困难。如文献[7-9]中列出的强碱滴定一元弱酸的滴定误差计算式分别为:
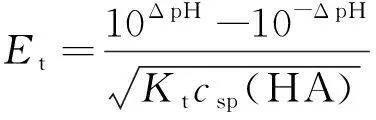
这两个公式在表达形式上是明显不同的。
对于强碱滴定混合弱酸和强碱滴定多元弱酸的滴定误差公式,很多文献[4-6]是按多元弱酸的分布系数来讨论的,而以林邦公式的形式来表达的滴定误差公式较为少见。
本文通过引入副反应和副反应系数的概念,对强碱滴定一元弱酸、混合弱酸和多元弱酸的滴定误差公式的推导进行了讨论,得出了相应的以林邦公式形式表达的滴定误差计算式并给出了实例。
1 有关强碱滴定强酸或弱酸的滴定误差公式推导
1.1 强碱滴定强酸的滴定误差公式
如用NaOH 滴定c(HA)mol/L强酸HA,有关化学反应为:
OH-+H+=H2O
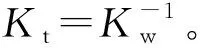
用林邦公式表达的终点误差公式为:
(1)
1.2 强碱滴定一元弱酸的滴定误差公式
如用NaOH滴定c(HA)mol/L弱酸HA,有关化学反应为:
OH-+HA=A-+H2O
1) 分布系数表达的滴定误差公式。
滴定终点产物为NaA,其PBE为:
[OH-]=[HA]+[H+]
(2)
终点误差为:
(3)
式(3)可变形为:
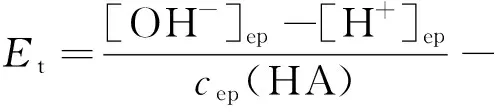
(4)
δ(HA)为弱酸HA的分布系数。
2) 林邦公式表达的滴定误差公式。
推导方法一:将强碱滴定弱酸的反应看成是有副反应参与的中和反应。


(5)
设A-对H+的副反应系数为α(H(A)),定义:

(6)
由式(6)得:
c(H+)=α(H(A))[H+]
代入式(5)中得:
(7)
依定义:
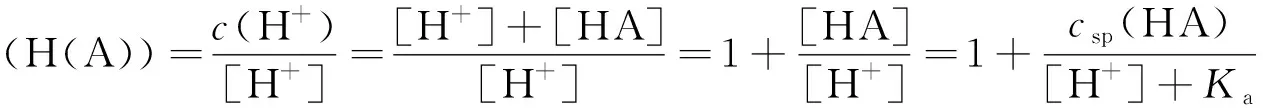
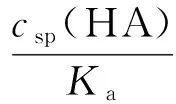
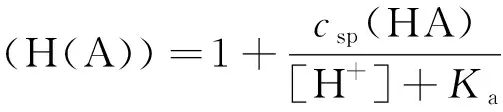
(8)
将式(8)代入式(7),得:
(9)
(10)
式(10)即强碱滴定一元弱酸时以林邦公式形式表达的滴定误差公式。
推导方法二:滴定反应为:
OH-+HA=A-+H2O
化学计量点时产物为一元弱碱NaA,溶液中的[OH-]按最简式计算。
(11)
将式(11)代入强碱滴定强酸的滴定误差公式中,得:
1.3 强碱滴定混合弱酸的滴定误差公式
设用强碱NaOH滴定强酸HA和HB,且离解常数Ka(HA)>Ka(HB)。
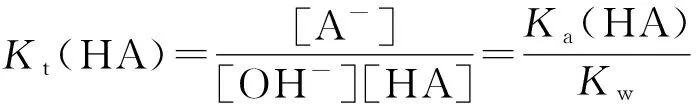
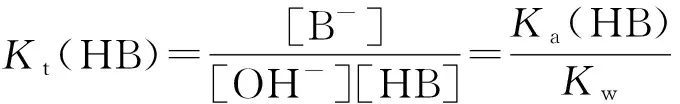
将HB与NaOH的反应作为HA与NaOH反应的副反应,主反应的平衡常数为Kt(HA′)。
主反应: OH-+HA=A-+H2O
副反应: OH-+HB=B-+H2O
(12)
依定义:
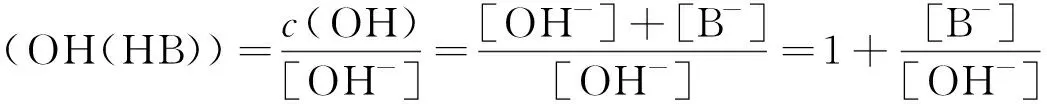
(13)
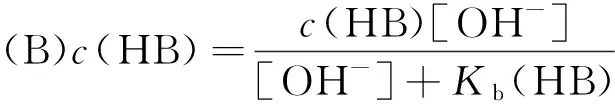

(14)
将式(14)代入式(12)中,得:
(15)
将式(12)中的Kt(HA′)代入
中的Kt(HA)中,得:
(16)
式(16)即强碱滴定混合弱酸的滴定误差公式。
1.4 强碱滴定多元弱酸第一化学计量点时的滴定误差公式
设NaOH滴定二元弱酸H2A,可看成是滴定一元弱酸H2A和HA-的混合酸。
有关反应为:
OH-+H2A=HA-+H2O,平衡常数为Ka1。
OH-+HA-=A2-+H2O,平衡常数为Ka2。
当Ka1≫Ka2,且在第一化学计量点csp(H2A)=csp(HA-)时,将Ka1、Ka2、c(H2A)和c(HA-)代入式(16),得:
(17)
式(17)与文献[7]中给出的公式(2-51)完全一致。
2 强碱滴定一元弱酸和多元弱酸的滴定误差计算应用示例
例1 以酚酞为指示剂,计算0.2mol·L-1NaOH滴定等浓度HAc的终点误差,设酚酞的变色点为pH=9.0。
解:已知csp(HAc)=0.1mol·L-1,[H+]ep=10-9,[OH-]ep=10-5,Ka=1.8×10-5,Kt=1014。
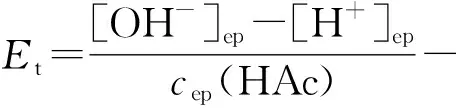
解法2:化学计量点时产物为NaAc,计算得pHsp=8.87。
ΔpH=pHep-pHsp=9.0-8.87=0.13
将所有已知条件代入式(10),得:
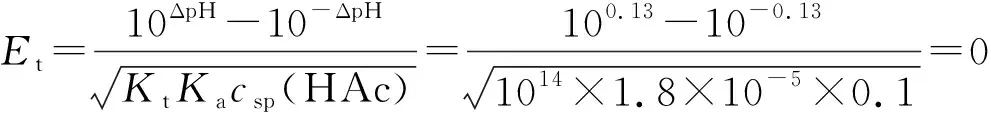
可见,使用式(4)和使用式(10)的计算结果完全相同。
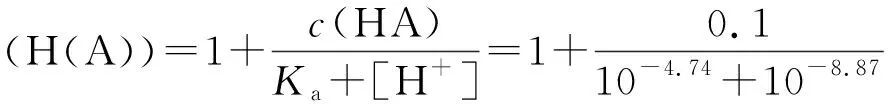
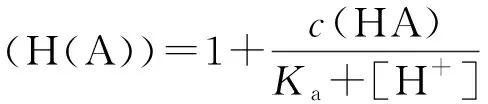
说明式(8)的近似处理是合理的。
例2 计算0.050mol·L-1NaOH滴定0.050mol·L-1H3PO4(pKa1=2.16,pKa2=7.21)至甲基橙变黄(pH=4.4)的终点误差。
按两性物质pH计算公式,第一化学计量点时溶液中[H+]为:
则:
ΔpH=pHep-pHsp=4.4-4.74=-0.34
按式(17)计算,则:
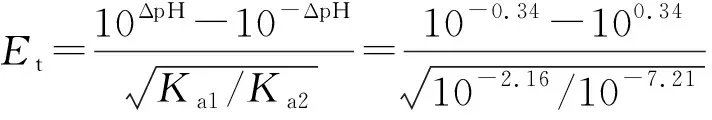
在教材中,副反应概念一般是在酸碱滴定法之后的络合滴定法一章中提出,因此,在讲授酸碱滴定误差公式时引用副反应概念,学生难以接受;可以在讲完络合滴定中副反应概念和定义后,再来讲授上述有关公式的推导过程。在上述推导中,引入的副反应不属于教材中定义的络合副反应、酸效应和共存离子副反应等副反应的范畴,但同样可以借用副反应系数的定义来计算。在讲授时强调这一点可以让学生更为灵活地理解和掌握副反应及副反应系数的概念和应用。上述实例的计算结果说明本方法推导的滴定误差公式是合理的。
参 考 文 献
[1] 王园朝.大学化学,2010,25(3):16
[2] 李英杰,时建朝,侯广顺.化工时刊,2011,25(2):42
[3] 刘彦明.信阳师范学院学报(自然科学版),1998,11(1):57
[4] 林训忠.湘南学院学报,2007,28(5):59
[5] 张宏,郝凌云.安徽师范大学学报(自然科学版),1999,22(2):184
[6] 杨伟群.化学与黏合,2007,29(1):68
[7] 武汉大学.分析化学.第4版.北京:高等教育出版社,2002
[8] 华中师范大学,东北师范大学,陕西师范大学,等.分析化学.第3版.北京:高等教育出版社,2002
[9] 周性尧,任建国.分析化学中的离子平衡.北京:科学出版社,2000
