简单碰撞理论的一种推导方法

刘国杰 黑恩成

(华东理工大学化学系 上海 200237)

自学之友

简单碰撞理论的一种推导方法

刘国杰 黑恩成

(华东理工大学化学系 上海 200237)

摘要设想双分子气体反应是由硬球分子先活化、再反应的模式进行，不仅能使简单碰撞理论(SCT)的推导变得更为简便，而且阈能和Arrhenius活化能等概念也变得更加明确。

关键词简单碰撞理论 阈能 活化分子 活化能

碰撞理论建立于20世纪初，是最常用的基元反应速率理论之一。由于当时量子力学还未进入化学领域，这个理论的模型十分简单，它将分子视为没有内部结构的硬球，将双分子气体反应看作硬球间的有效碰撞事件。但是即使如此，推导也不简单，特别是有效碰撞数的计算，它要引入阈能和反应截面等概念，使反应速率常数公式的推导较为复杂。本文旨在介绍另一种推导方法，它不仅比较简便，而且能从不同的视角加深对这个理论的认识。

1 反应速率常数

首先，与过渡状态理论相类似，设想反应A+B→P是以下列模式进行：

式中A和B为两个硬球反应物分子，P为产物分子，A*和B*分别为A和B的活化分子，它们是由反应物分子碰撞所致。

假设活化分子A*和B*很容易失去能量而蜕变成一般的硬球分子A和B，也就是说，A*和B*的浓度很低，它们转变成产物P的速率很慢，以致A*与B*有足够的时间与一般分子A和B建立平衡关系。即：

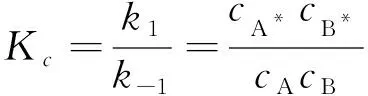
(1)

式中Kc为平衡常数。因此，根据平衡态近似，反应速率可表示为：

(2)

反应速率常数当为：

k=k2Kc

(3)

将式(3)取对数，得：

(4)

然后，再对温度求导，并代入Van′t Hoff方程：

(5)

式中ΔrUm为一般硬球分子转变成活化分子时的系统标准摩尔热力学能的增量，其值即为反应活化能E。积分式(5)，则得：

(6)

由于E=0时，A*和B*蜕变为A和B，此时，k=k2，故积分常数C=0。于是，式(6)变为：

(7)

或

(8)

因此，只要得知k2，便可导得简单碰撞理论的反应速率常数表示式。

2 k2的表示

首先应该指出，k2是两个活化分子A*和B*碰撞反应的速率常数，按照这个理论，其反应速率应为活化分子A*与B*的碰撞数，这是因为活化分子A*与B*一旦发生碰撞，则每一次碰撞都会反应生成产物P，故有：

(9)

式中ρA*为活化分子A*的数密度，ZA*B*为活化分子A*与B*的碰撞数。

其次应该指出，活化分子A*和B*与一般分子A和B的区别仅在于前者的能量高于后者，至于活化分子的质量和大小与一般分子没有区别，因为这些分子都被认为是刚性的硬球。故它们的碰撞截面和折合质量也与一般分子没有两样，且ZA*B*的推导方法也与ZAB完全一样，因各教材的推导大同小异，这里不再重复，而将推导结果直接列出如下：

(10)

式中σAB=π(rA+rB)2，称为碰撞截面，其中rA和rB分别为硬球分子A和B的半径。式中μ=mAmB/(mA+mB)为AB分子对的折合质量，其中mA和mB分别为硬球分子A和B的质量。式中kB为Boltzmann常量。

将式(10)代入式(9),可得:

(11)

由于ρA*=LcA*，ρB*=LcB*，代入式(11)后便得:

(12)

式中L为Avogadro常量。据此，可得活化分子A*与B*转变成产物P的反应速率常数为:

(13)

因此，将它代入式(8)，即得反应速率常数:

(14)

3 反应活化能与阈能

如果将式(14)与熟知的简单碰撞理论(SCT)反应速率常数公式[1]

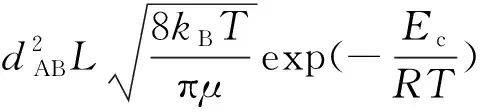
(15)

相比较，并注意到dAB=rA+rB(dAB称为平均碰撞直径)，则两者完全一致。可见阈能Ec在数值上与反应活化能E完全相等。即：

Ec=E

(16)

这从不同的视角赋予阈能以更明确的意义，它实际上相当于使一般硬球分子变成活化分子所必须提供的标准摩尔热力学能。由于硬球分子没有内部运动，且硬球之间又没有相互作用，故这个标准摩尔热力学能仅与碰撞时相对平动能有关，它是名副其实的反应活化能。

在不少物理化学教材中，常将Arrhenius活化能Ea当作化学反应的活化能，其实，这是有条件的，只有在k2不随温度而变时才是如此。在我们的前文[2]中，已经指出了这一点，本文则再次加以强调。

已知Arrhenius活化能的定义式为：

(17)

将式(14)代入这个定义式，不难得到:

(18)

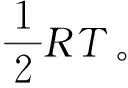
(19)

(20)

(21)

故Arrhenius活化能不仅仅是A和B分子活化所需的摩尔能，而且也包括了活化分子A*与B*反应成产物P所需的摩尔能，其中E或Ec才是名副其实的活化能。

此外，前文[2]已导出，Arrhenius活化能Ea与反应活化能E间的关系为:

Ea=nRT+E

(22)

参 考 文 献

[1] 傅献彩，沈文霞，姚天扬，等.物理化学(下册).第5版.北京:高等教育出版社，2005

[2] 刘国杰，黑恩成.大学化学,2013,28(2):77

上海高校重点教改项目(No.YJ0230201)；华东理工大学网络教育教改项目(No.WJY2011021)