基于广域测量系统的电力系统低频振荡的抑制研究
2013-09-22杨培宏张玉杰
刘 斌 杨培宏 张玉杰
(内蒙古科技大学信息工程学院,内蒙古 包头 014010)
随着全国互联电网规模的不断扩大,电力系统稳定问题使得人们备受关注。其中,低频振荡问题已逐渐趋于主要研究对象,给电力系统的安全稳定运行带来了严重的破坏,有待急需解决[1-2]。
发电机励磁控制是维持机端电压恒定和并联运行机组之间的无功功率合理分配,同时也是改善和提高电力系统稳定性的最经济有效的方法之一。同步发电机的励磁控制系统一般采用自动电压调节器(Automatic Voltage Regulator, AVR)和电力系统稳定器(Power System Stabilizer, PSS)的组合[3]。AVR是利用对机端电压的负反馈来保证电压调节的精度,PSS是通过在励磁侧引入附加信号,增加系统阻尼来抑制其振荡。现有的对PSS调参方式是基于在有限的范围内线性控制上的,而对于目前电力系统运行点处的线性化数学模型是无法保证其抑制效果[4]。
为此,电力系统的在线辨识低频振荡模态得到广泛研究。目前对于电力系统的低频振荡信号分析的方法有很多,主要有傅里叶算法、小波变换、Prony算法、卡尔曼滤波法以及希尔伯特—黄(Hilbert Huang Transform, HHT)方法等。傅里叶变换方法是一种在频域范围内的分析方法,对非平稳信号的处理将无能为力,且存在无法反映振荡的阻尼特性及瞬时频率的缺点。小波变换是在时频范围内分析信号的时频特性,能辨识多个振荡模态的变化规律,但小波基的选择难度很大,对辨识的结果有一定的影响。Prony算法可以精确的辨识系统的主导振荡模式,能够得到低频振荡的参数,但其计算速度有待提高,且受噪声的影响很大。卡尔曼滤波法能够消除噪声的影响,但在噪声的不同形式下滤波的效果也是有所差别,反映不出振荡信号的阻尼特性[5]。HHT方法是利用经验模态分解(Empirical Mode Decomposition, EMD)将信号分解为若干个固有模态函数(Intrinsic Mode Function, IMF)之和,然后对每个IMF分量进行希尔伯特变换,得到信号的瞬时频率和瞬时幅值,即Hilbert谱。然而,根据EMD分解的本质,容易产生端点延拓现象。这使得EMD分解得到的IMF分量失去了物理意义,不能完全表现出低频振荡信号的模态特征。
本文采用一种端点极值包络延拓算法来抑制其端点效应,该方法是一种把信号端点处的近似值作为端点处的极值点的处理方法,能够较好的处理EMD分解产生的端点效应现象,分解出电力系统低频振荡的信号模态,表征电力系统的阻尼特性。根据此法辨识的结果,利用粒子群优化算法来整定PSS参数,构建出最佳的励磁阻尼控制器,使其在不同的振荡模态下能够提供最佳的阻尼,达到最优效果。
1 在线辨识低频振荡模态
1.1 HHT方法的改进
Hilbert-Huang变换(HHT)是一种分析非线性、非平稳的信号分析方法,其核心是经验模态分解(EMD),将原始信号分解为一系列固有模态函数(IMF),然后得到信号的Hilbert谱。此方法能够克服传统信号分析方法的一些不足,但是在 EMD过程中容易出现端点效应现象[6]。
针对这一现象,本文采用端点极值包络延拓算法来有效的弥补 EMD分解中存在的端点效应,其方法改进如下:
1)由信号序列端点处的信号变换趋势判定出在此处是极大值还是极小值。
2)根据判定出的结果取相应的极值点来进行拟合求得拟合函数。
3)求出此函数在端点处的函数值。
采用多项式拟合算法来求极值点的拟合函数,其中拟合多项式的求解方法步骤如下:
1)根据信号特征,确定拟合多项式的次数n;
2)计算出sr和tr

3)得出正规方程组

4)解正规方程组求出a0,a1,…,an
5)写出拟合多项式

对于初始信号序列 x(t)找出它的所有极大值点和极小值点,然后分别利用分段幂函数对极大值和极小值点序列进行插值,形成 x(t)的上下包络线。数据序列 x(t)的两端中任一点,只能是极大值点或极小值点[7]。只要确定了断点处的极值就可以有效的避免端点效应。
利用端点极值包络延拓方法对测试信号:

进行信号延拓,再对其进行 EMD分解得到信号的各个IMF分量,如图1所示。

图1 改进HHT算法的测试信号分解
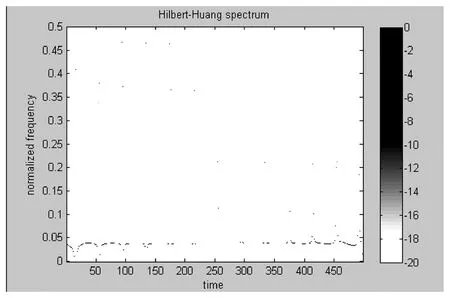
图2 测试信号的Hilbert谱
由图中可以看出,端点极值包络延拓方法能够使在信号端点处得上下包络误差较小,提高了均值曲线提取的准确性,因而使得Hilbert谱的分辨率也有所提高,有效的解决EMD存在的端点效应现象,得到单一的振荡模态,并且减少了信号的能量损失。
1.2 低频振荡信号模态分量的Hilbert变换
对于任一连续的时间信号 x(t),有如下 Hilbert变换:

由x(t)和y(t)可得到解析信号为

式中,a(t)为瞬时幅值;θ(t)为相位,则

瞬时频率为

在电力系统中,某一振荡模态分量均可表示为

式中,A为瞬时幅值;λ为衰减系数;ω为振荡频率;φ为初相位。
由控制理论可知,X(t)可写成如下表达式:

式中,ξ为阻尼比,由下列关系可表示为
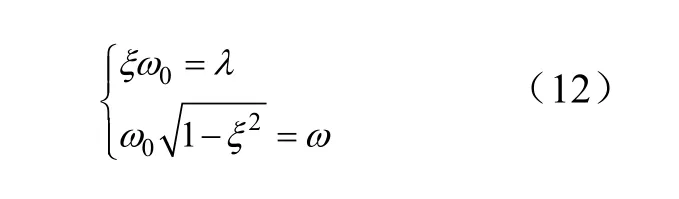
可得到阻尼比ξ为

2 附加阻尼励磁控制器的设计
由于低频振荡的产生是由系统缺乏阻尼或系统负阻尼引起的输电线上的功率波动,所以在控制方面有两方面因素:①调整控制措施,减小其带来的负阻尼;②通过附加控制增加系统的振荡模态阻尼[8-9]。本文对于低频振荡的信号是通过广域测量系统(Wide Area Measure System, WAMS)来进行采集,然后与传统的PSS在设置参数方面进行对比,设计出附加励磁阻尼控制器。

图3 广域测量系统的附加励磁阻尼控制器原理
如图3可知,该控制器是由模态辨识和PSS参数设置两部分组成,传统的附加励磁阻尼控制器在参数优化的过程中,利用特定的优化算法对阻尼特性作为目标函数,而没有考虑到控制器对振荡模态的影响,本文采用先对模态进行辨识与分析,然后对其中的PSS进行参数整定,有效的与本机的励磁系统相结合,可增加系统阻尼,抑制低频振荡的发生。因此采用粒子群优化算法来对PSS参数进行优化,该算法普遍应用性好,具有较强的全局搜索能力,避免了复杂的遗传操作[14-16]。通过各微粒的目标函数,在找到两个最优值—Pbest与Gbest时,对每个粒子按照如下公式进行更新:
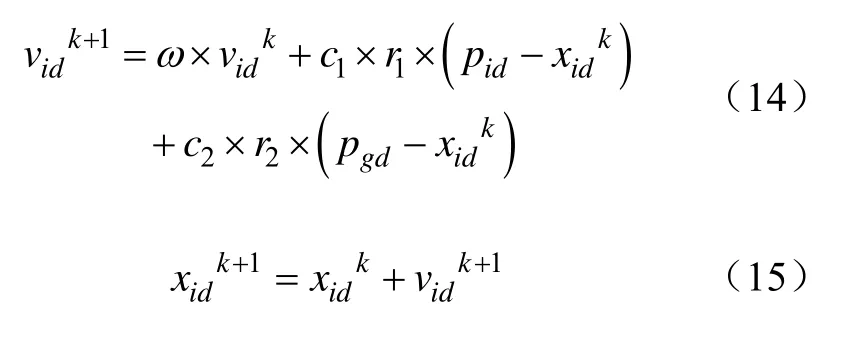
式中,i=1, 2, …, M为粒子总数;d=1, 2, …, N为空间的维数;为粒子的速度向量;为粒子当前位置;pid为粒子最优解的位置;pgd为种群最优解的位置;ω为惯性权重;C1和C2为加速常数。
若群体中所有粒子所经过的最优解位置为pg,则粒子的最优位置可由下式确定:
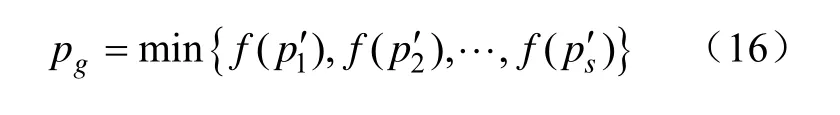
整个算法的步骤如下:
1)对粒子群进行初始化:分别对群体规模M,空间维数N,每个粒子的位置、速度进行初始化。
2)计算粒子的当前适应值。
3)更新粒子的极值:对选出最好的粒子代入式(14)、(15)计算速度和位置。
4)对全局极值进行优化:从全体极值中选出最优解,作为粒子的最优解位置。
5)更新当前粒子的速度和位置:再次代入式(14)、(15)更新每粒的速度和位置。
6)检查能否满足终止条件,若满足,则计算结束;否则,转至步骤2)。
3 仿真与分析
算例采用Kunder的两区四机系统,系统具体参数见文献[17],该系统由两个对称区域组成,每个区域各有两台900MVA的发电机,区域1的有功负荷为967MW,无功负荷为100Mvar,区域2的有功负荷为 1767MW,无功负荷为100Mvar,采用的运行方式为区域1向区域2输电,此系统容易发生低频振荡。系统结构图与励磁控制原理结构图如图 4所示。

图4 四机两区域系统图
传统的 PSS参数是在固定的运行模式下来调节,而本文中是基于广域测量系统的在线辨识,故在发电机G1和G3上均安装 PSS来改善系统的阻尼,PSS的参数取:
Ki=20,Tw=5,T1=0.05,T2=0.02
在上述系统中施加扰动后,将某一发电机的转速波动作为测试信号,辨识结果见表1。

表1 低频振荡模态分量参数
由上图可以看出,系统振荡存在3个模态,且阻尼比较弱,下面根据粒子群优化算法来优化 PSS参数,其中隔直环节的时间常数Tw、T1t、T3t为固定值,则优化后的PSS参数见表2。

表2 优化后的PSS参数
励磁系统中的PSS参数优化后,系统的阻尼会明显增加,令交流双回路的其中一条发生跳闸故障,持续时间为0.1s,在PSS参数优化后的机组输出振荡图如图5所示。

图5 发电机G1转速振荡图
由图中可以看出,附加阻尼控制器中的PSS在参数优化的情况下能有效的抑制发电机的转速波动,增强了系统的阻尼。
4 结论
在励磁控制器中,PSS参数的调节是抑制系统低频振荡的主要措施之一,本文基于希尔伯特—黄方法的低频振荡信号分析,能够正确的反映出振荡信号的非线性、非平稳的特征,并根据信号模态特征采用粒子优化算法在线计算系统的阻尼比,进而正确的设计出附加励磁阻尼控制器,通过仿真证明了该控制器能有效的抑制电力系统低频振荡,提高系统的安全稳定性。
[1] 朱振青.励磁控制与电力系统稳定[M].北京:中国电力出版社, 1994.
[2] 朱方,赵红光,刘增煌,等.大区电网互联对电力系统动态稳定性的影响[J].中国电机工程学报, 2007, 27(1):1-7.
[3] 阮阳,袁荣湘.采用输出反馈方式的电力系统非线性励磁控制[J].中国电机工程学报, 2011, 31(34): 68-76.
[4] 袁季修.电力系统安全稳定控制[M].北京:中国电力出版社, 1996.
[5] SWIFT F J, WANG H F. The Connection between Modal Analysis and Electric Torque Analysis in Studying the Oscillation Stability of Multi-machine Power Systems. Electrical Power and Energy Systems.1997, 19(5): 321-330.
[6] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal. Society of London Series A, 1998(31): 417-517.
[7] 韩松,何利铨,孙斌,等.基于希尔伯特—黄变换的电力系统低频振荡的非线性平稳分析及其应用[J].电网技术, 2008, 32(4): 56-60.
[8] 刘世宇,谢小荣,张东辉,等.附加励磁阻尼控制对励磁系统常规功能的影响[J].电力系统自动化, 2008,32(10): 6-9.
[9] 张帆,徐政.附加励磁阻尼控制抑制次同步谐振研究[J].电力系统自动化, 2007, 31(23): 24-29.
[10] 苏玉香,刘志刚,李东敏,等.一种改善 HHT 端点效应的新方法及其在电能质量中的应用[J].电力自动化设备, 2008, 28(11): 40-45.
[11] 李天云,高磊,赵妍.基于HHT的电力系统低频振荡分析[J].中国电机工程学报, 2006, 26(14): 24-30.
[12] KAMWA I, BELAND J, TRUDEL G, et al. Wide-area monitoring and control at Hydro-Quebec: past, present and future[C]//Proceedings of IEEE Power Engineering Society General Meeting. Montreal,Canada: IEEE-PES, 2006: 1-7.
[13] 杨德昌.基于改进希尔伯特-黄变换算法的电力系统低频振荡分析[J].中国电机工程学报, 2011.
[14] 赵辉,刘鲁源,张更新.基于微粒群优化算法的最优电力系统稳定器设计[J].电网技术, 2006, 30(3): 32-35.
[15] EL-ZONKOLY A M, KHALIL A A, AHMIED N M.Optimal Tuning of Lead-Lag and Fuzzy Logic Power System Stabilizers Using Particle Swarm Optimization.Expert Systems with Application. 2009.
[16] 荣雅君,贾艳,刘琳,等.基于粒子群优化算法的电力系统稳定器设计[J].继电器, 2008, 36(4): 23-26.
[17] KUNDER P. Power system stability and control [M].New York: McGraw-Hill, 1994: 703-708.
