重力梯度张量的预条件共轭梯度法反演

陈少华，朱自强，鲁光银，曹书锦

(中南大学 地球科学与信息物理学院，湖南 长沙，410083)

重力勘探方法在区域地质调查、成矿远景区划分评价、水文及工程地质勘察等方面发挥重要作用。常规重力勘探只观测重力位的铅垂一阶导数，而重力梯度勘探则观测重力位的二阶导数，因此，相比传统的重力测量，重力梯度测量有更高的分辨率[1]，更能够清晰地反映场源体边界形态，且其张量数据较为丰富，能够提高异常体的解释精度。作为一种前沿性的重力测量方法，国外学者不仅对重力梯度测量仪器进行了大量开发，还对采集的数据进行了大量研究。Zhang等[2]利用欧拉反褶积法解释了重力全张量数据；Zhdanov等[3]利用重加权正则化共轭梯度法，采用聚焦正则化对目标函数进行约束，数值模拟表明该算法对尖锐边界有较强的反演效果；Wilson等[4]针对巨大的航空重力梯度测量数据，采用并行算法，利用共轭梯度法对其进行反演，该算法在Vredefort得到了具体应用。此外，国外对重力张量数据的去噪、谱分析等方面的研究也取得了一定的成果[5-7]。在国内，姚长利等[8]针对三维物性反演中存在的困难和问题，提出三维物性反演的随机子域方法技术；郭良辉等[9]提出了基于重力梯度数据异常分离的三维相关成像方法提高成像分辨率,数值模拟结果表面该方法能够使重力梯度数据具有良好的横向及纵向分辨率。与国外相比，国内对这一方面的研究较少，目前还没有开发出重力梯度张量测量仪器，对重力梯度张量数据的解释也较少。相较于非线性反演方法，线性反演算法出现的时间较长，应用较为广泛。传统线性反演算法中雅可比矩阵的存储需占用大量内存，计算该矩阵与其转置相乘将耗费大量时间且占用大量内存，而共轭梯度法只要计算两次雅可比矩阵与向量的乘积[10-11]，计算时间将大量减少且所需内存小，有利于大规模计算。针对雅可比矩阵的条件数较大而产生病态解的问题，首先对方程组进行预条件处理[12-13]，通过减小该矩阵的条件数来增强线性方程组的稳定性。本文作者在目标函数中加入粗糙度函数及深度加权函数，利用预条件共轭梯度法对目标函数进行反演，数值模拟结果证明了反演的有效性；针对重力梯度张量采集的数据有5个分量是独立的，充分利用重力梯度张量数据的丰富性，利用5个独立分量进行反演，取得了较好的效果。

1 正演

首先，在笛卡儿坐标系下(图1)，设地面上某点O为坐标原点。根据万有引力定律，一个剩余密度为ρ、体积为V的地质体，其在外部空间任意一定产生的引力位为：

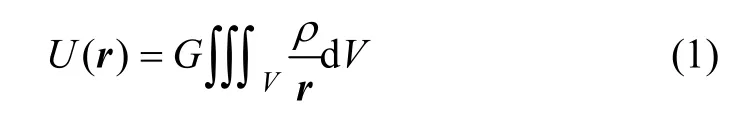
式中：r为观测点 P(x,y,z)到异常点 Q(ξ,η,ζ)的矢量；G为万有引力常量。

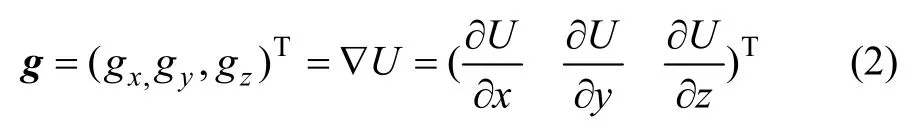
式中：g，gx，gy和gz均为笛卡儿坐标系(x,y,z)的函数；g为U(r)的一次导数；U(r)的二阶导数可表示为：

由于在地球外部，位场满足拉普拉斯方程Gxx+Gyy+Gzz=0，以及重力场的无旋性：Gxy=Gyx，Gxz=Gzx，Gyz=Gzy，因此，在重力梯度张量中只有5个分量是独立的。

图1 笛卡儿坐标系下的长方体模型及地下空间剖分Fig.1 Rectangular model and subsurface division in Cartesian coordinates

将探测区域的地下空间离散成一系列大小相等的长方体[14]，赋予每个小长方体1个固定的剩余密度，在探测区域建立笛卡儿坐标系(图1)，x轴指向正北方向，y轴指向东方向，z轴垂直向下，则地面任意观测点各梯度分量的异常值可表示为：

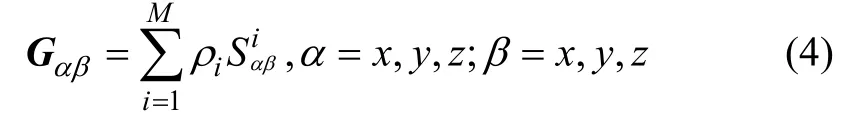
式中：iSαβ代表某重力梯度分量中第i个长方体的几何架构，称为位置函数；ρi为第i个长方体的剩余密度；M为所划分长方体的个数。

则由地下空间离散的所有长方体在地面所有观测点产生的重力梯度异常值满足线性关系：

2 反演

2.1 粗糙度约束

重力梯度张量的反演便是求解线性方程组(5)。由于采集的数据向量d远少于要反演的未知数m，因此该反演是个欠定问题，方程组的解不唯一且不稳定，必须对目标函数加上适当的约束来缩小解的范围。本文中通过引入粗糙度函数[15]，来对模型空间进行约束，目标函数可表示为：

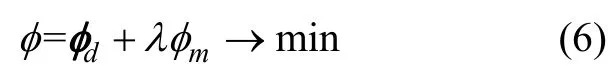
定义模型粗糙度R为m(r)在x，y和z方向一阶偏微分的平方和，即

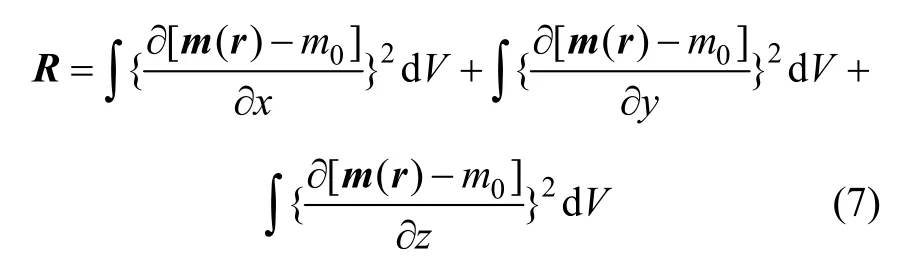
2.2 深度加权

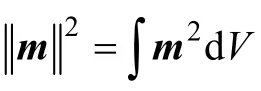
式中：z为块体单元中心点埋深；z0和β为常数。β一般情况下取 2～4；z0取决于块体单元的尺寸以及观测面的高度。

将式(8)及最小化模型构造代入式(7)：

式中：αs，αx，αy和 αz为模型目标函数中各项的加权因子。

对式(9)按照模型区域的网格剖分进行离散化，用有限差分代替微分算子，写成如下矩阵形式：

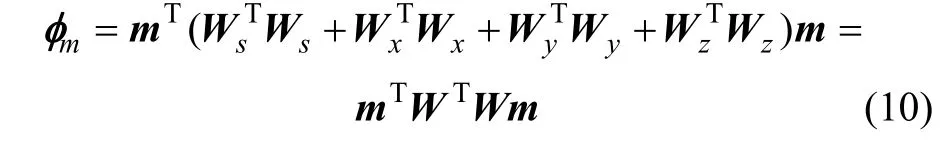
每一个矩阵分量都可以写成2个独立的矩阵与1个系数矩阵的乘积，即

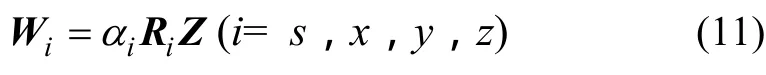
式中：Ri为有限差分算子；Z为离散化的深度加权对角线矩阵。将式(10)代入式(6)：

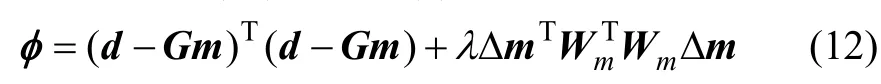
式(12)可写成方程组：

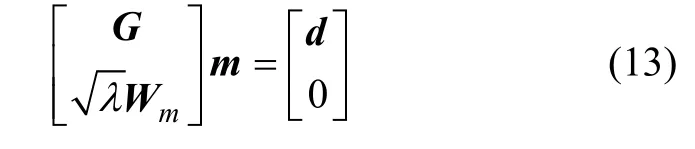
式(13)可写成：

2.3 预条件共轭梯度法

由于模型参数的规模较大，在实际计算中，收敛的次数越少越好，而方程的收敛速度由雅可比矩阵的条件数决定的。位场中雅可比矩阵的条件数通常巨大，同时，van Decar等[18]指出在目标函数中增加粗糙度约束将减缓收敛速度，为了避免过多的收敛次数及增强解的稳定性，将常规的方程AtAm=Atb改进成：

因此，预条件共轭梯度法的计算步骤：

(1) 给定初始值ε，令m0=0；k=0；r0=Atb；

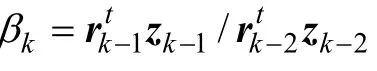
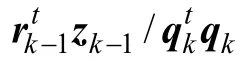
(4) 计算 rk=rk-1-αkAtqk，若||rk||2＜ε，则停止计算，否则返回第(2)步。

其中：S为预条件因子。若 S≈(AtA)-1，则 SAtA≈I(其中，I为单位矩阵)，那么预条件因子S就可以大大改善式(14)的条件数，使得特征值集中分布在对角线附近，有效地提高迭代速度，这便是预条件共轭梯度法。但是，这样求解S是非常困难的，在实际应用中，用简单的深度加权函数即式(8)作为预条件因子[12]，能很好地改善式(14)的条件数，实际模型反演结果证明了这一点。

3 数值模拟

3.1 单分量反演

将场源空间划分为20×20×10=4 000个单元格，每个单元格沿x，y和z轴方向的长度均为50 m。如图2所示，地下空间存在2个异常体，2个异常体的长×宽×高均为200 m×200 m×200 m，异常体顶板埋深均为125 m，底板为325 m，异常体的剩余密度为1.0 t/m3。总共有20×20=400个采集数据，数据采集点位于表层，沿x和y轴间距都为50 m。

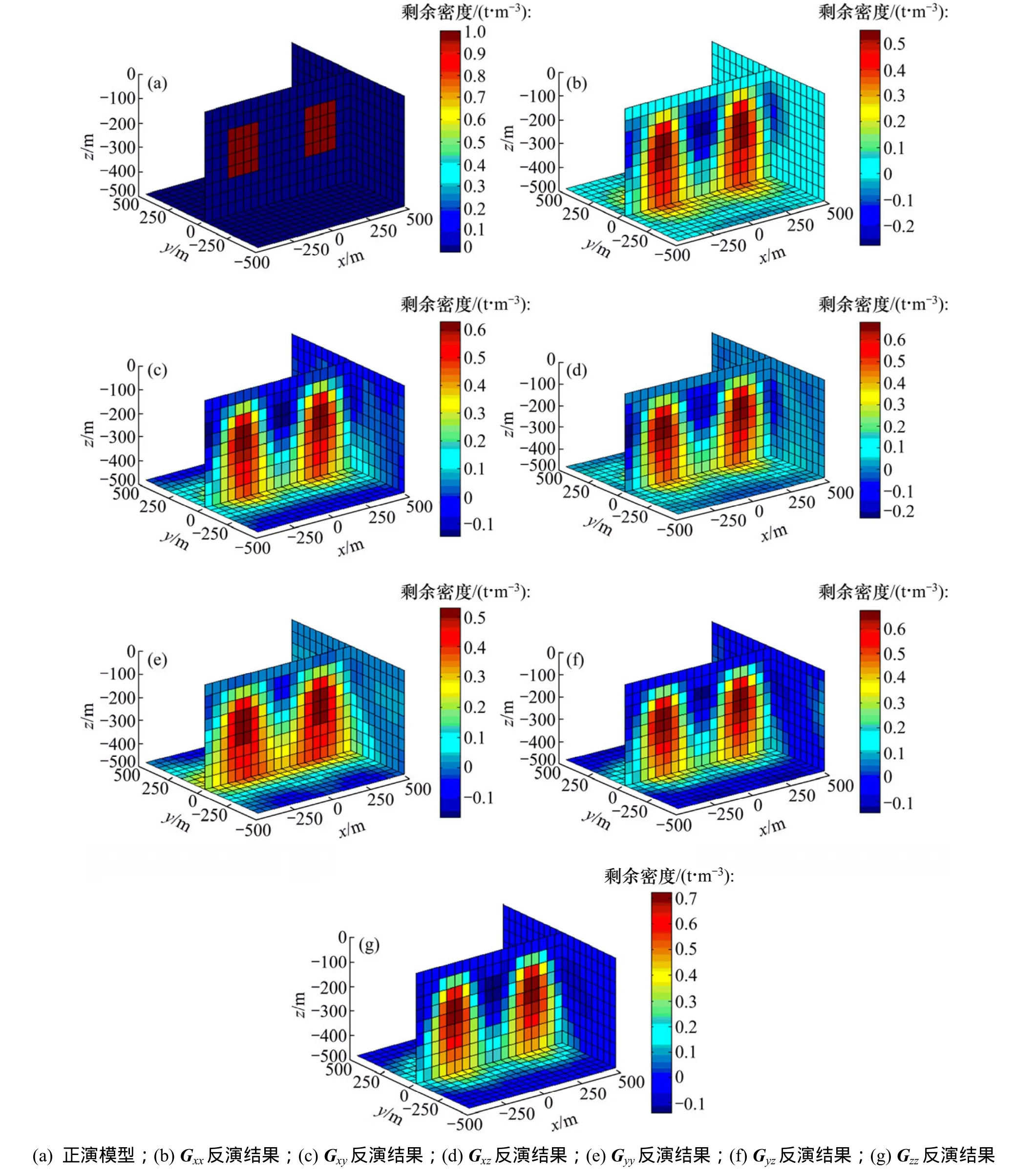
图 2 正演模型和 Gxx，Gxy，Gxz，Gyy，Gyz和Gzz的反演结果Fig.2 Forward model and inversion results of Gxx, Gxy, Gxz, Gyy, Gyz and Gzz

定义绝对拟合差：

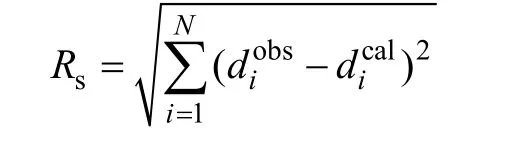
反演参数的设置中，取 αx=αy=αz=1，αx=0.00 005，z0=20，β=4，收敛终止的条件是上一次迭代的绝对拟合差大于后一次的绝对拟合差。从以上各个单分量反演结果可知：每个分量基本能够反演出异常地质体的位置和形态，反演出来的剩余密度也都不同程度地接近真实值，但都出现了大小不等的负值，其中以 Gxx和 Gxz出现的负值较大，而 Gxy，Gyy，Gzz和 Gyz反演出来的负值相对较小；同时可知Gxx，Gxz，Gxy和 Gyy分量的反演结果较为发散，在深度方向上的延伸较大，不能完全反演出异常点的位置；而Gyz及Gzz分量的反演结果集中于异常体周围，且准确地反映了目标体的深度。

为了各个分量的比较，定义相对拟合差Rms：

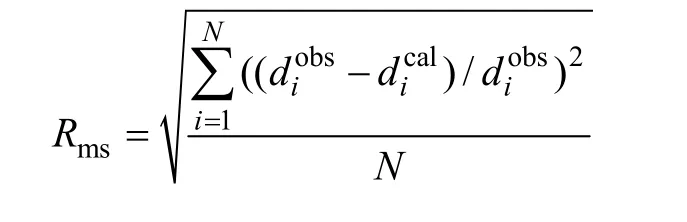
图3所示为各个分量在不同迭代次数下的相对拟合差。从图3可知：Gxz分量的反演非常不稳定，随着迭代的进行Rms上下波动比较厉害，Gxx分量也出现了小范围的上下波动，这可能是以上2个分量反演结果中出现较大负值的原因；Gxy及Gyy分量基本上随着迭代的进行 Rms逐渐变小，但减小的速度较慢，最终其Rms仍然较大；Gyz及Gzz分量不仅随着迭代的进行Rms快速减小，而且最终的Rms也比较小。

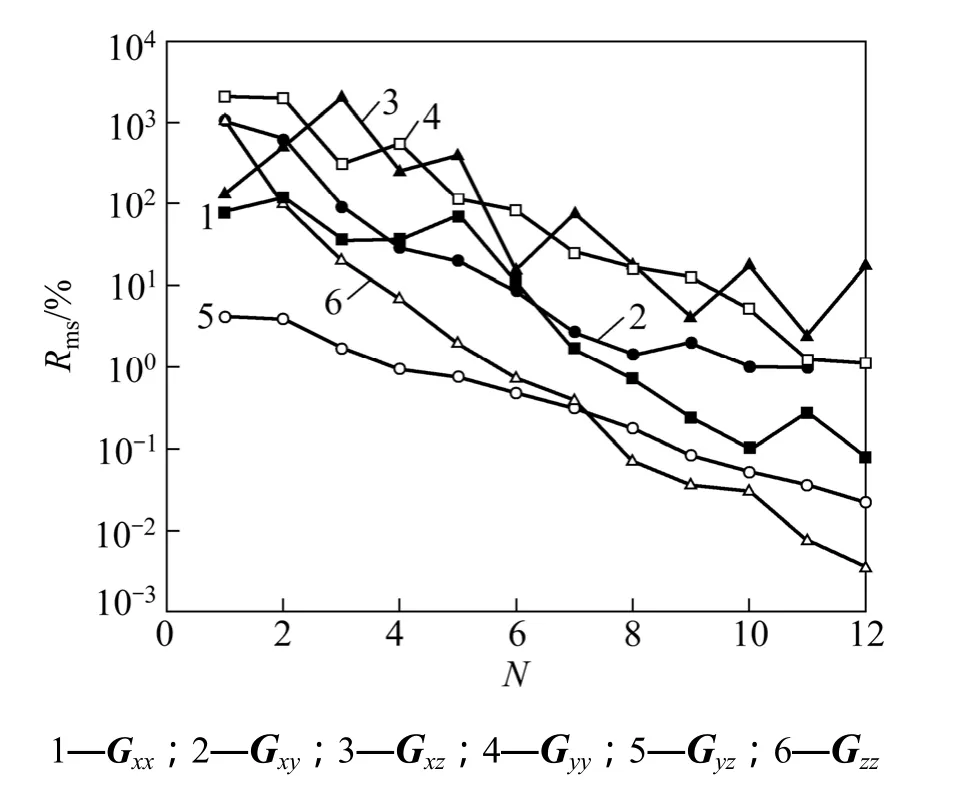
图3 各个分量在不同迭代次数下的相对拟合差Fig.3 Relative misfit of all single component in different numbers of iteration

3.2 全张量反演

虽然理论上可以证明同一方法不同分量并不能改变由位场性质决定的多解性[19]，这由于引起位场多解性的一个重要原因是数据的不完整和不精确，而观测得到的数据总是受限于一定网格距和一定的精度。尽管如此，同一高度不同分量的观测数据在完整性上仍有所补充，并减少了误差引起的多解性。重力梯度张量相比于重力勘探，不仅有更高的分辨率，还在于其更为丰富的数据量，充分利用5个独立分量的信息将有利于提高反演的精度。

本文采用5个独立分量Gxx，Gxy，Gxz，Gyy及Gzz进行联合反演，并对反演数据加入10%的噪声干扰，检验反演的抗噪性能。取 αx=αy=αz=1，αs=0.000 05，z0=10，β=4，虽然随着迭代的进行，数据的绝对拟合差能不断地降低，但可能导致过拟合而引起多余构造，故本次收敛中取最多的迭代次数为30次，观测数据的正演模型见图2(a)。

与没有加入高斯噪声的图 2中各个单分量相比较：图4(a)所示的反演的异常体不仅集中，而且和异常体的真实深度吻合，验证了同一种方法的不同分量的联合反演可以减少多解性，提高解的精度。图4(b)中加入 10%的高斯噪声后反演的异常形态仍较为明显，只是在异常体的周围出现一些小异常，但可以忽略不计，表面5个分量联合反演有较好的抗噪性。

3.3 合成模型反演

现设计1个Y型岩脉，该模型曾被姚长利等[8-9,20]应用于位场相关领域的分析。图5(a)和(b)所示分别为深度120 m的深度切片和图5(a)中A-A′的断面切片，图5(c)所示为120 m深度剖面的反演结果，图5(d)所示为图5(a)中A-A′断面切片的反演结果，白色方框为真实异常体的位置。异常区Ⅰ(颜色较浅)的异常体其剩余密度为0.8 t/m3，深度方向延伸不大；异常区Ⅱ(颜色较深)的异常体其剩余密度为1.0 t/m3，深度方向延伸大，两岩脉的延伸方向相反。将地下空间剖分为20×20×10=4 000个长方体，每个长方体的大小都为50 m×50 m×50 m。正演计算的观测点位于地表处，共有20×20=400个观测点，在观测数据中加入3%的高斯噪声，采用5个独立分量对地下异常体进行联合反演。

反演参数的设置中，取 αx=αy=αz=1，αx=0.000 05，z0=20，β=4，最多迭代次数为30次，加入先验参数范围约束，当解小于0时令其为0，当解大于1.1时令其为1.1。整个反演过程的迭代次数为30次，消耗的时间为21.742 587 s，相对拟合差为0.026 371。

图 5(c)所示较好地反映了异常体的形态和位置，左边岩脉的形态和位置基本吻合，右边岩脉沿y轴方向完全吻合，在x轴方向稍微扩大了一点，但基本上与异常体的真实形态一致；图5(d)中基本重构出了模型的异常形态，其异常走向与Y型岩脉一致；结合图5(c)和5(d)可发现：反演算法在浅部取得了较清晰的结果，而在深部反演的分辨率则有所下降，表明虽然基于深度加权的重力梯度张量反演能够使物性的参数值大致能够分布在相应的位置，但重构模型的分辨率不可避免地随着深度的增加而降低。以上结果表明：基于粗糙度约束和深度加权的重力梯度张量反演，能够在一定程度上较好地重构模型的异常形态。

4 结论

(1) 提出了基于预条件共轭梯度法的重力梯度张量反演，收敛速度快，耗时较短，可用于数据量较大的反演计算。

(2) 相对于单分量反演，充分利用 5个独立分量的信息进行联合反演，能够较准确地反演出异常体的形态及剩余密度特征。

(3) 仅用理想模型数据对本文的算法进行了验证，需要进一步采用现场采集的数据进行验证。

[1] 曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005:68-71.ZENG Hualin. gravitational field and gravitational prospecting[M]. Beijing: Geological Publishing House, 2005:68-71.

[2] Zhang C, Mushayandebvu M F, Reid A, et al. Euler deconvolution of gravity tensor gradient data[J]. Geophysics,2000, 65(2): 512-520.

[3] Zhdanov M S, Ellis R, Mukherjee S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data[J]. Geophysics, 2004, 69(4): 925-937.

[4] Wilson G, Cuma M, Zhdanov M S. Massively parallel 3D inversion of gravity and gravity gradiometry data[J]. Preview,2011, 152(6): 29-34.

[5] Lyrio L S, Tenorio L, Li Y G. Efficient automatic denoising of gravity gradiometry data[J]. Geophysics, 2004, 69(3): 772-782.

[6] While J, Jackson A, Smit D, et al. Spectral analysis of gravity gradiometry profiles[J]. Geophysics, 2006, 71(1): J11-J22.

[7] Afif H. Understanding gravity gradients: Atutorial[J]. The Leading Edge, 2006, 25(8): 942-947.

[8] 姚长利, 郑满元, 张聿文. 重磁异常三维物性反演随机子域法方法技术[J]. 地球物理学报, 2007, 50(5): 1576-1583.YAO Changli, ZHENG Manyuan, ZHANG Yuwen. 3-D gravity and magnetic inversion for physical properties using stochastic subspaces[J]. Chinese Journal of Geophysics, 2007, 50(5):1576-1583.

[9] 郭良辉, 孟晓红, 石磊, 等. 重力和重力梯度数据三维相关成像[J]. 地球物理学报, 2009, 52(4): 1098-1106.GUO Lianghui, MENG Xiaohong, SHI Lei, et al. 3-D correlation imaging for gravity and gravity gradiometry data[J].Chinese Journal of Geophysics, 2009, 52(4): 1098-1106.

[10] 吴小平, 汪彤彤. 利用共轭梯度方法的电阻率三维反演的若干问题研究[J]. 地震地质, 2001, 23(2): 321-327.WU Xiaoping, WANG Tongtong. Study on some problems for 3D resistivity inversion using conjugate gradient[J]. Seismology and Geology, 2001, 23(2): 321-327.

[11] 吴小平, 徐国明. 利用共轭梯度法的电阻率三维反演研究[J].地球物理学报, 2000, 43(3): 420-427.WU Xiaoping, XU Guoming. Study on 3-D resistivity inversion using conjugate gradient method[J]. Chinese Journal of Geophysics, 2000, 43(3): 420-427.

[12] Pilkington M. 3-D magnetic imaging using conjugate gradient[J].Geophysics, 1997, 62(4): 1132-1142.

[13] Pilkington M. 3D magnetic data-space inversion with sparseness constraints[J]. Geophysics, 2009, 74(1): L7-L15.

[14] 骆遥, 姚长利, 薛典军, 等. 2.5D地质体重磁异常无解析奇点正演计算研究[J]. 石油地球物理勘探, 2009, 44(4): 487-493.LUO Yao, YAO Changli, XUE Dianjun, et al. Analytic singularity-free forward computation of gravity and magnetic anomaly for 2.5-D geologic body[J]. Oil Geophsical Prospecting,2009, 44(4): 487-493.

[15] Constable S C, Parker R L, Constable C G. Occam's inversion: A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3):289-300.

[16] Li Y G, Oldenburg D W. 3-D inversion of magnetic data[J].Geophysics, 1996, 61(2): 394-408.

[17] 姚姚. 地球物理反演基本理论与应用方法[M]. 武汉: 中国地质大学出版社, 2002: 57-59.YAO Yao. Basic theory and application of geophysical inversion methods[M]. Wuhan: China University of Geosciences Press,2002: 57-59.

[18] van Decar J, Snieder R. Obtaining smooth solution to large,linear, inverse problems[J]. Geophysics, 1994, 59(5): 818-829.

[19] 管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005:199-204.GUAN Zhining. Magnetic field and magnetic exploration[M].Beijing: Geological Publishing House, 2005: 199-204.

[20] Li Y G, Oldenburg D W. 3-D inversion of gravity data[J].Geophysics, 1998, 63: 103-119.