高速轧机工作界面非稳态润滑过程界面动力学特性
2013-09-21王桥医陈娟高瑞进赵勇
王桥医,陈娟,高瑞进,赵勇
(1. 杭州电子科技大学 机械工程学院,浙江 杭州,310018;2. 西南铝业(集团)有限责任公司,重庆,401326)
金属轧制界面非稳态润滑系统动力学研究[1-2]实际上包括2个方面:一方面为非稳态摩擦润滑理论,另一方面为系统动力学分析。国外学者对处于不同润滑状态(全膜润滑,混合润滑及边界润滑)的金属塑性加工过程稳态摩擦润滑机理已进行了广泛的研究[3-6]。国内学者近年来也一直致力于金属塑性加工摩擦润滑理论及系统动力学方面的研究[7-9],但他们一般仅考虑稳态摩擦润滑对轧机系统动力学的影响。然而,许多金属成型过程本身是瞬间非稳态的,有些稳态过程由于振动而变成非稳态。人们对于金属成型过程的非稳态润滑机理研究甚少,尤其是对轧机辊缝之间的非稳态润滑摩擦及润滑摩擦对轧机系统动力学的影响的研究还远远不够,没有形成一套完整的理论。有实验表明非稳态润滑是产生轧机垂直振动的主要因素之一[10-14],但很少有人对此通过理论分析来解释非稳态润滑现象及导致颤振发生的原因。对于非稳态润滑系统或结构处于振动状态的金属成型过程,过程参数是与时间有关的,因此,问题变得较复杂。为此,本文作者综合运用轧制理论、流体力学理论、摩擦润滑理论,建立考虑非稳态润滑过程轧机系统力学模型,该模型综合运用界面摩擦模型、轧制力、轧制力矩模型、流体动力润滑模型构成的多重耦合模型,定量分析高速轧机工作界面非稳态润滑过程界面动力学特性。
1 工作界面非稳态润滑模型
在混合润滑中,轧件和轧辊表面粗糙度高度分布一般认为是高斯分布。为方便起见,Christensen等[15]提出了1个简化了的公式来近似代替高斯分布,则某一特定高度z的概率密度函数f(z)为


式中:h为两接触表面的间隙,又称为名义油膜厚度。
在轧制过程中,工作界面的润滑状态多为混合润滑。变形区油膜厚度是描述界面摩擦状态的1个重要参数,板带与轧辊之间的间隙是流体动压力的挤压作用而形成。乳化液的压应力分布可由雷诺方程式确定:

图1 Christensen表面粗糙度的接触示意图Fig.1 Sketch map of surface roughness profile of Christensen


变形区油膜厚度h(x)与入口油膜厚度h0需满足流量连续条件,即

式中:h0为入口油膜厚度;u1为入口轧件速度;u(x)为轧件速度;v为轧辊表面线速度;r为压下率。
2 工作界面摩擦模型
如图2所示,Timoshenko等[16]给出了基于直角坐标系统的von Mises屈服准则:



图2 基于直角坐标系统的屈服准则Fig.2 Coordinate system for yield criterion
可以写为:

在轧辊对称中心线处,假设τxy=0,在轧件和轧辊界面处,τxy=τs(其中,τs为表面剪切应力),于是,τxy可以表示为:

式中:c是常量,且0≤c≤1。当c=0时,平均剪切应力为0;当c=1时,平均剪切应力等于表面剪切应力。因为库仑摩擦定律在高负载条件下对于金属成形过程是不适用的,因此,引入Wanheim等[17]提出的摩擦因数模型:

式中:m为摩擦因数。
将式(9)和(10)中的τxy和sτ代入式(8),得到平面应变条件下的屈服准则:

当考虑材料均匀变形时,可以忽略式(8)中剪切应力的影响,从而得到下面简化了的屈服准则:

3 工作界面应力分布
图3所示为轧件中任取的一个微单元体。微单元体的厚度是dx,受到张应力σx、压应力p和剪应力τs作用。假设φ很小,则沿着x轴方向的静力平衡方程可以表示为:

将


图3 微单元体受力图Fig.3 Stress acting on a vertical slice
代入式(13)的静力平衡方程中,即得von Kárámn公式:

在轧制过程中,在任何一点x的应力分布的一阶微分方程可以写为:

式中:xc为工作辊中心水平位移;R为工作辊半径。应用边界条件为

水平应力可以写成:
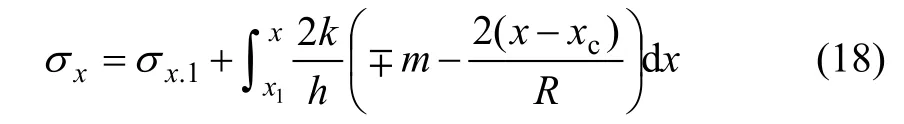
运用式(18),在出口处的水平应力可以表示为

4 轧制力和轧制力矩模型
用沿着接触弧轧制力的直接积分法,可以获得描述轧制力计算的新公式。首先考虑 von Mises平面应变屈服准则,在式(8)中假设

则式(12)可以重新写为:

将式(18)中的σx代入屈服公式(21),得到:

式中:x2≤x≤x1;x1为轧件入口处坐标,x2为轧件出口处坐标。
单位宽度的轧制力仅仅是p和在x方向或是y方向的轧辊咬入剪应力τs的积分。因为摩擦力在中性点处改变符号,因此,有必要分为2步进行积分。沿着x轴和y轴方向单位宽度轧制力可以写为:

式中:

考虑到摩擦力在中性点处将改变符号,如图4所示,其中,xn为中心点坐标。由轧辊和带材之间的摩擦力引起的作用于轧辊的轧制力矩可以通过沿着接触弧摩擦力的积分计算。在轧辊咬入的带材内部,剪切应力的分布如图4所示。由图4可见:作用于轧辊上的剪切应力和作用于带材上的剪切应力方向是相反的。定义z轴正方向为垂直于纸面向外,则作用于上工作辊的轧制力矩为

图4 作用于上工作辊的摩擦力Fig.4 Friction acting on top work roll

5 计算结果及讨论
图5和图6所示分别为在不同的压下率下,摩擦应力和压应力的分布。对于较小的压下率(r=0.200 0~0.215 0),摩擦应力很小,其最大值发生在入口和出口的边缘处。这是因为:油膜压应力在较小的压下率时变化非常小,因此,润滑油膜的黏度实质上是恒定的,于是,速度的差异决定了摩擦应力的分布,速度的变化在工作区的边缘最大。

图5 不同压下率下界面摩擦应力分布Fig.5 Friction stress distribution for various reductions

图6 不同压下率下界面压应力分布Fig.6 Pressure distribution for various reductions
在较大的压下率下(r=0.217 5~0.230 0),压力黏度的影响很大。因此,由于摩擦效应引起的轧制力的上升,导致在工作区润滑剂剪切应力的上升,并达到极限剪切应力。
图7和图8所示分别为在不同时刻工作区压力和摩擦应力的分布情况。仿真中无量纲角频率为2π,故张应力变化的完整周期大约在T=1.00到T=2.00之间。所以,选择进行对比的无量纲时间T分别为1.25,1.50,1.75,这时张应力分别处于最高值、平均值和最低值。在较大的张应力(T=1.25)条件下,在工作区,压应力低,油膜剪切应力小,压力梯度也相当小。摩擦应力在进口和出口边缘达到最大,因为界面间相对滑动速度在这些点处最大;随着张应力(T=1.50,1.75)的减小,油膜压力增大,剪切应力增大更快,最终达到润滑油抗剪强度。图7和图8所示验证了轧制过程的非稳态润滑现象,对于更复杂的情况,不难预测压应力和摩擦应力在不同时刻的分布情况。

图7 不同时刻工作区压应力分布Fig.7 Pressure distribution in work zone at different time

图8 不同时刻工作区摩擦应力的分布Fig.8 Friction stress distribution at different time
图9所示为在压下率是0.200 0和0.250 0,表面粗糙度分别为0,1和10 µm时总轧制力的变化。当全膜润滑(Rq=0)或者表面粗糙度(Rq=1 µm)很小时,轧制力的平均值和轧制力的变化幅度随着压下率的增大而增大,轧制力的最小值几乎是一样的,不受表面粗糙度和压下率变化的影响。
图 10所示为不同的压下率和表面粗糙度时轧制力矩的变化。轧制力矩的变化趋势和轧制力的变化趋势非常相似。然而,对于带材表面粗糙糙度(Rq=10)很大的轧制过程,轧制力矩的变化幅度比轧制力的变化幅度小。

图9 不同压下率和表面粗糙度下轧制力的变化Fig.9 Roll force variation for various reduction and surface roughness

图10 不同压下率和表面粗糙度下轧制力矩的变化Fig.10 Roll torque variation for various reduction and surface roughness
6 结论
(1) 综合运用轧制理论、流体力学理论、摩擦润滑理论,建立了考虑非稳态润滑过程轧机系统力学模型。该模型综合运用了界面摩擦模型、轧制力、轧制力矩模型、流体动力润滑模型构成的多重耦合模型,定量分析了高速轧机工作界面非稳态润滑过程界面动力学特性。
(2) 当压下率较小时,摩擦应力很小,最大值发生在入口和出口的边缘处。油膜压应力在较小的压下率时变化非常小,速度的差异决定了摩擦应力的分布,速度的变化在工作区的边缘最大。
(3) 在较大的张应力下,在工作区压应力低,油膜剪切应力小,压力梯度也相当小。摩擦应力在进口和出口边缘达到最大。随着张应力的减小,油膜压力增大,剪切应力增大更快,最终达到润滑油抗剪强度。
(4) 在全膜润滑或者表面粗糙度很小的情况下,轧制力的平均值和轧制力的变化幅度随着压下率的增大而增大,轧制力的最小值几乎是一样的,不受表面粗糙度和压下率变化的影响。轧制力矩的变化趋势和轧制力的变化趋势非常相似。然而,对于带材表面粗糙糙度很大的轧制过程,轧制力矩的变化幅度比轧制力的变化幅度小。
[1] LI Hongguang, MENG Guang. Effect of boundary condition on a self-excited vibration system with clearance[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2007,8(4): 571-583.
[2] WANG Zhanghai, WANG Dejun. Method of judging the self-excited vibration of rolling main drive system in rolling slippage[J]. Journal of Sound and Vibration, 1998, 215(5):1135-1143.
[3] Saniei M, Salimi M. Development of a mixed film lubrication model in cold rolling[J]. Journal of Materials Processing Technology, 2006, 177(1): 575-581.
[4] Stephany J, Ponthot P. Effect algorithmic approach for mixed-lubrication in cold rolling[J]. Journal of Materials Processing Technology, 2004, 153(2): 307-313.
[5] Pair N, Cheng H S. An average flow model for detecting effects of three dimensional roughness on partial hydrodynamic lubrication[J]. Tans ASME, 1978, 100(1): 12-18.
[6] Tonder K. The lubrication of unidirectional striated roughness:Consequences for some general roughness theories[J]. ASME,Journal of Tribology, 1986, 108: 167-170.
[7] 王桥医, 黄海军, 李志华. 金属塑性加工工作界面非稳态润滑轧机振动控制[J]. 中南大学学报: 自然科学版, 2010, 41(4):1418-1423.WANG Qiaoyi, HUANG Haijun, LI Zhihua. Control of mill vibration for unsteady lubrication based on metal-forming process[J]. Journal of Central South University: Science and Technology, 2010, 41(4): 1418-1423.
[8] 杨竞, 郭兴旺, 吴迪平. 非稳态轧制时轧机振动的形态与评判[J]. 北京科技大学学报: 自然科学版, 1999, 21(1): 64-66.YANG Jing, GUO Xingwang, WU Diping. Form and judgment of vibration of rolling mill in unstable state rolling[J]. Journal of University of Science and Technology Beijing: Science and Technology, 2001, 33(4): 64-66.
[9] 孙建亮, 彭艳, 刘宏民, 等. 四辊轧机辊系的横向自由振动[J].中南大学学报: 自然科学版, 2009, 40(2): 429-435.SUN Jianliang, PENG Yan, LIU Hongmin, et al. Free transverse vibration of rolls for four-high mill[J]. Journal of Central South University. Science and Technology, 2009, 40(2): 429-435.
[10] Swiatoniowski A, Bar A. Parametrical excitement vibration in tandem mills mathematical model and its analysis[J]. Journal of Materials Processing Technology, 2003, 134(1): 214-224.
[11] Perhua H U, ZHAO Huyue, Ehmann K F. Third-octave-model chatter in rolling chatter model[J]. Journal of Engineering Manufacture, 2006, 220(4): 1267-1279.
[12] Chang D F, Wilson W R D. Lubrication of strip rolling process in the low speed mixed regime[J]. Tribology Trans, 1996, 39(2):407-415.
[13] Yun I S, Wilson W R D, Ehmann K F. Review of chatter studies in cold rolling [J]. International Journal of Machine Tools and Manufacture, 1998, 38(12): 1499-1530.
[14] Swiatoniowski A, Bar A. Non-linear vibration in cold rolling mill[J]. Journal of Materials Processing Technology, 2003,134(2): 214-224.
[15] Christensen P, Everfelt H, Bay N. Pressure distribution in plate rolling[J]. Annals of CIRP, 1986, 35: 141-146.
[16] Timoshenko S, Goodier J N. Theory of elasticity[M]. 2nd ed.New York: McGraw Hill, 1951: 67-68.
[17] Wanheim T, Bay N. A model for friction in metal forming processing[J]. Annals of CIRP, 1978, 27: 189-198.
