旋转电磁致热器热功率与结构参数关系的研究
2013-09-20陈磊裴宇龙柴凤程树康
陈磊, 裴宇龙, 柴凤, 程树康
(哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨 150001)
0 引言
旋转电磁致热器,是一种新型电磁加热装置[1-2]。它从传统电机温升与损耗的反问题出发,将机电能量转换系统和以水为媒质的热交换系统有机地组合在一起,利用磁滞、涡流和二次感应电流综合加热水或其他流体媒质。其与电动机、风机、水轮机等动力机械装置配套使用,能实现电能、风能、水能等多种清洁能源的综合利用。除此之外,其内部的电磁场对流体媒质会产生磁化作用,使其物化特性发生有益的改变[3-6]。旋转电磁致热器可广泛应用于供暖、洗浴、水处理、海水淡化等场合。
致热器的设计方法与传统电机既有联系又有区别。传统电机中电磁场的分布规律和计算方法在致热器中仍然适用,借此可以对致热器的电磁场展开计算,得出其热功率的计算方法[7-10]。区别在于电机设计时往往力求减少单位体积内的损耗,以提高电机的效率;而在致热器设计时,损耗变成了有益的热功率,应力求增加单位体积内的热功率(热功率密度),以降低致热器的成本。本文将分析致热器热功率的分布规律,并以此为依据研究不同结构致热器在不同转速下,热功率密度的变化规律,为致热器的优化设计提供依据。
1 致热器热功率的分析
1.1 定子侧涡流热功率的分布情况
致热器运行时产生的热功率主要是定子侧的涡流、磁滞和二次感应电流热功率,其中磁滞热功率占的比率较小。从电磁感应的原理看来,涡流和二次感应电流热功率的产生原因是一致的,都是由旋转磁场切割导体感应出电势后产生的焦耳热。因此对致热器的热功率进行分析,可简化为对其定子侧涡流热功率的分析。
假设致热器定子材料唯一,为圆筒形,图1表示了其感生涡流展开图。
假定致热器中各电磁场量正弦分布,并且磁导率μ和电导率σ均为常数,根据电磁场中二维行波传播的理论可知定子内表面的电流密度可以表示为

其满足微分方程

由式(1)与式(2)可以得到
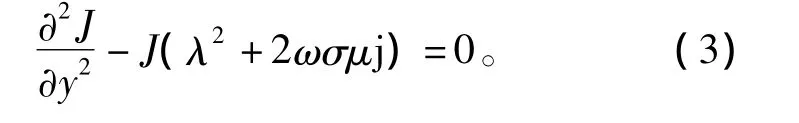
可得到电流密度的解为[10]

式中:τ为极距;ω为旋转角频率。
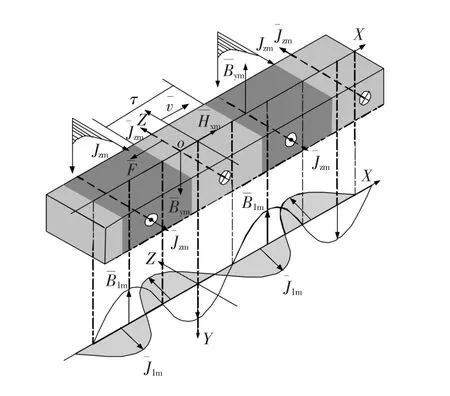
图1 旋转电磁致热器定子感生涡流展开图Fig.1 The developed mathematical model for eddy current of the REMH
由式(4)可以看出定子电流密度的幅值随着与气隙的距离y增加而下降。当y=2/α时,可算得此处电流密度的幅值仅为定子内表面的1/e2,由于涡流热功率与电流密度幅值的平方成正比,即此处涡流热功率仅是定子内表面处的1/e4,约为1.83%。因此可以定义d=2/α为致热器定子涡流热功率的透入深度,认为在y=2/α以外的定子区域已经没有涡流热功率。
极对数为p的致热器以转速n(r·min-1)旋转时,ω可按下式计算为

带入式(6),得到透入深度d的计算式为

极对数为9、定子材料为20号钢时,致热器定子电流密度透入深度与转速的关系如图2所示。即当定子材料和极对数一定时,透入深度与转速的平方根成反比。可以看出,在低速时和高速时,透入深度随转速变化呈现截然不同的规律:在低速段,透入深度随着转速的升高迅速下降;而到了高速段,透入深度随着转速的升高缓慢下降,变化很小。

图2 热功率透入深度与转速的关系曲线Fig.2 Correlation curve of penetration depth with rotational speed in transducer
1.2 热功率透入深度在致热器设计中的作用
根据电磁感应定律,感应电势E的大小与穿过导体回路磁通量Φ的变化率成正比,有

根据焦耳定律,感应电势在电导率为σ的材料中产生的焦尔热P应为

即在感应电势一定的情况下,焦尔热与导体材料的电导率成正比。在常见的电工材料中,铁(钢)的电导率较低,铜的电导率较高,因此在相同磁通的情况下,铜中的热功率密度应高于铁中的;但由于铜的磁导率又远低于铁心材料,仅依靠其自身构成的外磁路无法提供较高的磁通。因此要获得较高的热功率密度,需要将这2种材料合理地进行排布。
利用透入深度可以合理地对致热器定子进行设计:首先,由于透入深度之外的定子区域热功率非常微弱,当定子厚度高于透入深度时,超过的那部分定子厚度并不贡献热功率,会造成材料的浪费,降低致热器的热功率密度,因此透入深度是确定致热器定子厚度的重要依据。在设计时,可根据致热器的转速范围求得透入深度的范围,进而初步确定定子厚度尺寸。其次,透入深度反映了致热器定子磁通的渗入情况,透入深度越大,意味着磁通也透入得越深,那么可以在定子上相应位置布置铜材料,以求磁通和铜材料交链后得到更大的热功率。最后,由于透入深度在低速区和高速区有截然不同的特性,因此在设计时,一定要结合致热器的转速范围来进行合理的设计。
2 不同定子结构时热功率的分析
本节将以透入深度为依据,研究不同定子结构下,致热器热功率随转速的变化规律。采用二维时步有限元法对热功率进行计算[11]。在分析过程中,为方便比较,假定各部件的温度均为10℃,保持致热器的定子内外圆直径、气隙长度和转子结构和尺寸一定,致热器的基本参数见表1。其中定转子铁心材料均为20号钢,永磁材料为N33uH,铜条材料为Cu62。

表1 样机结构尺寸和材料Table 1 Demensions and materials of prototype
2.1 闭口槽结构
在致热器定子铁心中开孔后嵌入若干铜导条,并使用短路环使铜条在端部短接,这种类似于电机中闭口槽的结构,称之为闭口槽致热器。图3为其基本结构。

图3 闭口槽致热器结构Fig.3 Structure of closing-slotted heater
图4给出了铜条数目为12,直径分别为2、3、4 mm与定子仅有铁心时的致热器热功率数值比较。从图4中可以看出,嵌入铜条后,致热器的整机热功率在低速区和高速区呈现不同的趋势:在低速区,闭口槽结构的致热器热功率略高于纯铁心时的,而在高速区闭口槽结构的热功率低于纯铁心结构。低速时,随着铜条直径的增加,整机热功率上升,但随着转速的增加,到了高速区,整机热功率随着铜条直径的增加反而降低。在低速区,随着铜条数目的增加,整机热功率上升,高速区整机热功率随着铜条数目的增加反而降低。这两种高低速区不同的变化规律分界线大约在1 500 r/min左右,接近图2中透入深度与转速变化的拐点位置。
在转速较低时,磁通透入深度足够,能通过致热器的“轭部”完全与铜条交链,由于铜的电导率高于铁,此时铜条的体积越大,单位体积产生的热功率将变大,因此低速时铜条直径越大,致热器整机的热功率越高。随着转速的提高,定子涡流产生的去磁磁势不断增加,使磁通的透入深度越来越低,进而与导条交链的磁通也越来越少。此时由于铜条下方的槽口处磁通趋于饱和,铜条的存在增加了主磁路的磁阻,铜条的直径越大,主磁通将越低,因此高速时,铜条直径越大,致热器整机的热功率反而越低。
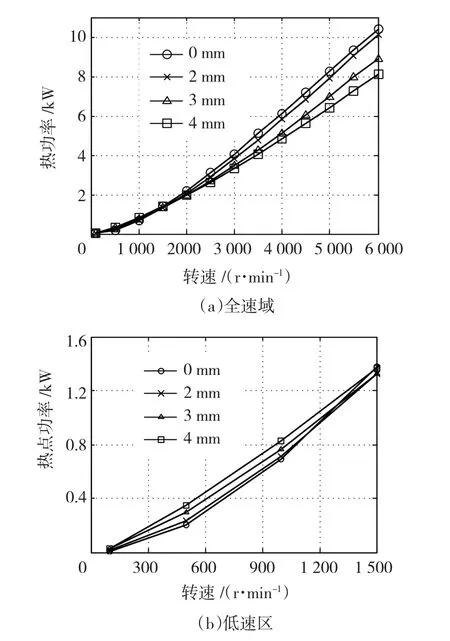
图4 闭口槽致热器热功率比较Fig.4 Thermal power comparison of closing-slotted heater
可以看出,闭口槽结构致热器热功率密度与透入深度密切相关。只有铜条布置在磁通能透入的铁心范围内,才能有效的提高整机的热功率密度。因此,在设计闭口槽致热器时,应先根据致热器的转速范围计算透入深度,当致热器转速较低时,磁通的透入深度足够,可在铁心中透入深度范围内布置一定量的铜条,来增加整机的热功率。
2.2 开槽结构
如前节所述,透入深度大时,与铜条交链的磁通足够多,才能发挥出铜电导率高的优势来增加整机热功率密度。因此考虑在定子上采用开槽结构,增大致热器切向磁通路径的磁阻,来提高定子磁通的透入深度,从而提高热功率密度。类似于电机,设计了开口槽和半开口槽2种结构的致热器,其转子结构和闭口槽一样,定子结构和槽型尺寸如图5和图6所示。开口槽结构在定子内圆开槽,铜条放置于槽内,并紧贴定子内圆安放,因此槽的宽度w和高度h均不能小于铜条的直径。半开口槽结构同样在定子内圆开槽,但槽的宽度w小于铜条的直径,为了放置铜条,在槽的顶端开与铜条大小相同的圆孔,将铜条放置与孔内,将定子内圆到铜条之间的最短距离称之为半开口槽的槽高h。

图5 开口槽结构示意图Fig.5 Diagram of opening-slotted structure

图6 半开口槽结构示意图Fig.6 Diagram of semi opening-slotted structure
图7给出了闭口槽和开槽结构致热器热功率的比较,开口槽和半开口槽结构尺寸与闭口槽结构的一致,铜条的直径均为3 mm,数量为12个。其中开口槽的槽宽和槽高均为3 mm,半开口槽的槽宽和槽高均为1 mm。

图7 开槽与闭口槽结构热功率比较Fig.7 Thermal power comparison of slotted and closing-slotted structure
从图7可以看出:在低速区,开槽结构的致热器热功率要高于闭口槽结构,其中开口槽结构的热功率最大,半开口槽结构的次之;在高速区,闭口槽结构的致热器热功率最大,半开口槽结构的次之,开口槽结构的最小。低速时,定子铁心中磁通的透入深度大,而且开槽结构增加了“齿部”的切向磁阻,使开槽结构的致热器较之闭口槽结构能有更多的磁通通过“轭部”与铜条交链,从而此时开槽结构整机的热功率要比闭口槽结构的大。由于开口槽结构比半开口槽结构的“齿部”切向磁阻更大,因此有更多的磁通通过“轭部”与铜条交链,从而导致开口槽结构的热功率要大于半开口槽结构的。高速时,定子铁心中磁通的透入深度非常小,已无法通过“轭部”与铜条发生交链,此时开槽反而相当于加大了等效气隙的长度,造成磁密下降,因此开槽结构的致热器热功率反而小于闭口槽结构的。而开口槽结构槽口比半开口槽结构的宽,因此其等效气隙也更大,故而在高速时开口槽结构的热功率最低。因此在实际设计时,如果致热器工作在低速区,可使用开口槽或半开口槽结构来增加整机的热功率密度。
下面讨论在铜条直径和数量不变的情况下,改变开口槽结构的槽高和槽宽,开口槽结构致热器热功率的变化情况。
图8表示了槽宽分别为3 mm、4 mm、5 mm和6mm时开口槽结构致热器的热功率。可以看出,在整个速度范围内,增加槽宽都使得热功率下降,可见,当槽口宽与铜条直径相同时,已经最大程度的增加了低速时磁通在铁心内的透入深度,在此基础上再增加槽宽,反而增加了等效气隙,造成热功率的下降。

图8 开口槽结构不同槽宽时热功率比较Fig.8 Thermal power comparison of different slot widths in opening-slotted structure
图9表示了槽深分别为3 mm、4 mm和5mm时开口槽致热器的整机热功率,从图中可以看出改变槽深对整机热功率几乎没有影响,因为只要“轭部”的厚度足够,不使磁通在轭部饱和,那么改变槽深几乎对磁路的磁阻没有影响,也就对热功率没有影响。因此在设计时,保证“轭部”磁通不饱和的前提下,适当的增加槽深,一是能够在不减少整机热功率的情况下减轻整机重量,从而提高了热功率/质量比;二是能够增加换热面积,有利于换热。但是开槽会增加气隙的谐波磁通,会在转子和永磁体表面产生出谐波热功率,因此在设计时要加以考虑。若这部分热量不能及时传给流体媒质,而造成永磁体温度的升高,反而会造成热功率的下降。
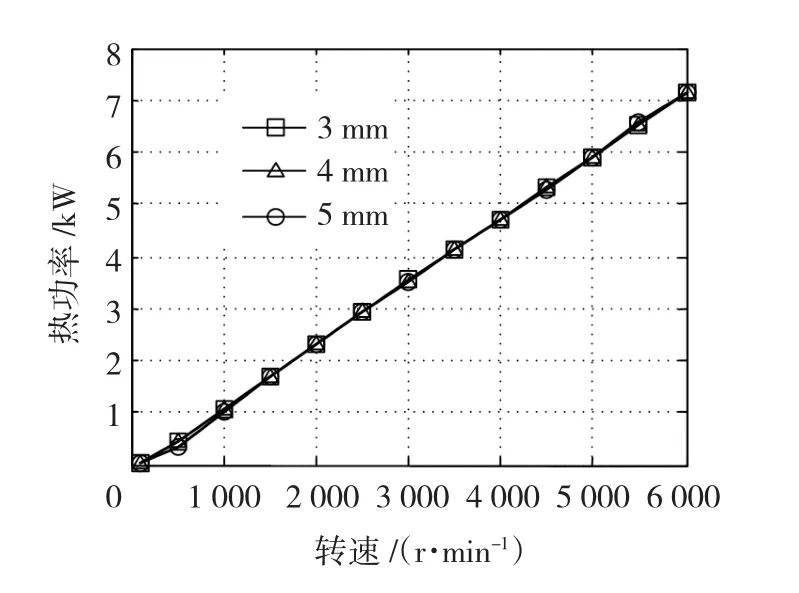
图9 开口槽结构不同槽深时热功率比较Fig.9 Thermal power comparison of different slot depths in opening-slotted structure
3 实验研究
用原动机拖动致热器旋转,测量输入转速和转矩即可计算得到其热功率值。致热器外端包裹隔热层,测试前让将恒温的水流流过,并监测出入水口的温度,当出入水口温度一致且长时间不发生变化,则认为内部达到了热平衡,各部分温度与水流的温度一致。此时用电机拖动致热器旋转待转速稳定即停下,认为这段时间,致热器内各部件的温度尚未发生变化,测得的热功率即为各部件温度与水流温度一致时的热功率。实验现场照片如图10所示。

图10 样机热功率测试平台Fig.10 Thermal power test platform of the prototype
本文实际研制了闭口槽和开口槽的样机各一台,样机定转子铁心材料均为20号钢,铜条材料均为紫铜Cu62,永磁材料均为N33uH,参数见表2。计算和测试时各部件温度均为10℃。图11比较了开口槽和闭口槽两种结构的热功率测试值,与前面仿真和理论分析的结果趋势一致,低速时开口槽的热功率要大于闭口槽的,高速时相反,交接点正好是在透入深度拐点附近。这证明了前面分析的正确性。

表2 致热器样机参数Table 2 Parameters of the prototypes

图11 样机热功率测试曲线Fig.11 Tested curve of thermal powers of the prototypes
4 结论
本文给出了其定子热功率透入深度的定义和计算方法,并分析了其在热功率设计中的作用。比较了不同定子结构的致热器在不同转速下热功率数值和分布的变化规律。得出结论如下:
1)透入深度是致热器设计的重要依据。致热器的热功率仅产生在定子透入深度以内,据此可以初步确定致热器定子厚度。进一步,可以在透入深度范围内布置铜材料,以求磁通与其交链后得到更大的热功率。
2)闭口槽结构在高速时热功率密度较大,而开槽结构在低速时热功率密度较大,在致热器实际设计时可据此按照转速范围合理地选择定子结构。
3)开口槽结构槽深对热功率没有影响,在设计时可以适当地增加槽深,以改善换热,降低整机重量,提高热功率/质量比。
[1]程树康,崔淑梅,李芙.动态电磁感应加热方式初探——电机与电器温升反问题研究[J].微电机,2005,38(1):68,33.
CHENG Shukang,CUI Shumei,LI Fu.Preliminary research on dynamic electromagnetic induction pyrogenation method—the research on the reverse problems of temperature rise of electric machines and appliances[J].Micromotors,2005,38(1):68,33.
[2]程树康,裴宇龙,张鹏.旋转电机第三功能初探[J].电工技术学报,2007,22(7):12-17.
CHENG Shukang,PEI Yulong,ZHANG Peng.Fundamental research on the third funtion of rotating electrical machine[J].Transactions of China Electrotechnical Society,2007,22(7):12-17.
[3]陈磊,侯云鹏,程树康.无焰加热器的结构及机理分析[J].微特电机,2008,36(11):4-6.
CHEN Lei,HOU Yunpeng,CHENG Shukang.Structure and mechanism analysis of flameless heater[J].Small&Special Electrical Machines,2008,36(11):4-6.
[4]CHENG Shukang,CHEN Lei,HOU Yunpeng.Fundamental research on flameless electromagnetic heater base on the reverse problem of temperature rise and loss in electrical machines[C]//2008 IEEE Vehicle Power and Propulsion Conference,Sep.4-6,2008,Harbin,China.2008:1168-1172.
[5]PEI Yulong,CHAI Feng,YU Yanjun.Analysis of novel rotating electromagnetic heater based on the concept of the third function of rotational motor[C]//The 11th International Conference on Electrical Machines and Systems,Oct.17-20,2008,Wuhan,China.2008:1142-1143.
[6]CHUNTING Mi,GORDON R Slemon,RICHARD Bonert.Modeling of iron losses of permanent-magnet synchronous motors[J].IEEE Transactions on Industry Applications,2003,39(6):734-742.
[7]吴新振,王祥珩,罗成.异步电机转子感应非正弦电流时的导条损耗[J].中国电机工程学报,2005,25(17):131-135.
WU Xinzhen,WANG Xiangheng,LUO Cheng.Loss calculation for induction machine rotor bar with non-sinusoidal current[J].Proceedings of the CSEE,2005,25(17):131-135.
[8]JOHN B.Goodenough.Summary of losses in magnetic materials[J].IEEE Transaction on Magnetics,2002,38(9):3398-3408.
[9]JUSSI Huppunen.High-speed solid-rotor induction machine electromagnetic calculation and design[D].Lappeenranta:Doctoral Thesis of Lappeenranta University of Technology,2004:35-41.
[10]裴宇龙.基于旋转电磁理论的机电热换能器及其相关参数的研究[D].哈尔滨:哈尔滨工业大学电气工程及自动化学院,2009:41-42.
[11]陈磊,柴凤,裴宇龙,等.新型旋转电磁热机三维电磁场方程的求解及相关电磁参数的研究[J].电工技术学报,2011,26(7):147-153.
CHEN Lei,CHAI Feng,PEI Yulong,et al.The solution of the 3D electromagnetic equation and research on related electromagnetic parameters of the novel rotational electromagnetic heating machine[J].Transactions of China Electrotechnical Society,2011,26(7):147-153.
