基于粒子群算法和卡尔曼滤波器的PID控制
2013-09-20王江荣李东旭
王江荣,李东旭
(1.兰州石化职业技术学院 信息处理与控制工程系,甘肃 兰州 730060;2.电子科技大学 生命与技术学院,四川 成都 611731)
0 引言
PID控制系统因其简单、稳定性好和可靠性高等优点,被广泛应用到工业过程控制中。PID控制器的性能取决于它的三个参数(比例、积分和微分)的整定是否合理,因此,优化PID控制器参数具有重要意义。但是PID参数的整定一般需要经验丰富的工程技术人员来完成,这种方法不仅费时,而且不能保证获得最佳性能。粒子群算法(Particle Swarm Optimization,PSO)是一种有效的全局寻优算法,本文将使用PSO对PID控制器的参数进行优化设计。另外,在有噪声干扰的控制系统中,噪声往往是非平稳随机过程,因其时变性,致使功率谱不固定。卡尔曼滤波(R.E Kalman)是一种具有最小无偏差性,适用于非平稳序列滤波的算法,它是能够剔除随机干扰误差,获取逼近真实情况的有用信息,且能自适应地处理观测值。基于此,本文建立了基于粒子群算法和卡尔曼滤波器的PID控制方法,有效地解决了PID控制系统中存在的参数的整定及控制干扰信号和测量噪声信号问题。仿真结果表明该方法具有良好的控制效果,明显地改善了系统的静态和动态特性。
1 基于粒子群算法的参数优化
粒子群优化算法(Particle Swarm Optimization,PSO)是Kennedy和Eberhart受鸟群觅食行为启发于1995年提出的一种全局优化算法[1-2]。PSO算法(一种仿生算法)具有搜索能力强、收敛速度快、设置参数少、程序易实现和无需梯度信息等特点。所有的粒子(搜索空间中的鸟)都有一个由被优化函数决定的适应值和一个决定它们运动方向和运动距离的速度,问题的解就是搜索空间中的一只鸟的位置。PSO算法的主要特点为:(1)每一粒子都被赋予了初始随机速度并在解空间中流动;(2)个体具有记忆功能;(3)个体的进化主要是它本身的飞行经验以及同伴的飞行经验进行动态调整,通过迭代找到最优解。在每一次迭代过程中,粒子通过追逐两个极值来更新自己的位置。一个是粒子自身所找到的当前最优解,这个解称为个体极值pbest;另一个是整个群体当前找到的最优解,这个解称为全局极值pbest
PSO 算法如下[3]:
设在一个D维搜索空间中,由n个粒子组成的种群X=(X1,X2,…,Xn),其中第i个粒子表示为一个D维的向量Xi=(xi1,xi2,…,xiD)T,代表第i个粒子在 D维搜索空间中的位置,亦代表问题的一个潜在解。根据目标函数即可计算出每个粒子位置Xi对应的适应度值。第 i个粒子的速度为 Vi=(vi1,vi2,…,viD)T,i=1,2,…,n。记第i个粒子搜索到的最优位置(即个体最优值pbest)为Pi=(pi1,pi2,…,piD)T;整个粒子群搜索到的最优位置(全局最优值gbest)为Pg=(pg1,pg2,…,pgD)T。当两个最优解都找到后,每个粒子根据下式来更新自己的状态。
粒子状态更新操作如下:

其中,vid(t+1)表示第 i个粒子在 t+1次迭代中第 d(d=1,2,…,D)维上的速度;w为惯性权重,η1,η2为加速常数(学习因子),rand()为0~1之间的随机数。此外,为使粒子速度不致过大,可设置速度上下限,即 vid∈[-vmax,vmax],vmax是之前设定的最大速率(边界值),t为当前迭代次数。Pt是粒子迄今为止搜索到的最优位置;Gt是整个粒子群迄今为止搜索到的最优位置。
用于参数估计的PSO算法具体实现过程如下:
(1)初始化粒子群,随机产生所有粒子群的位置和速度,并确定粒子的Pt和Gt。
(2)对每个粒子,将其适应值与该粒子所经历过的最优位置Pt的适应值进行比较,如较好,则将其作为当前的。
(3)对每个粒子,将其适应值与整个粒子群所经历过的最优位置Gt的适应值进行比较,如较好,则将其作为当前的Pt。
(4)按式(1)和(2)更新粒子的速度和位置。
(5)如果没有满足终止条件(通常为预设的最大迭代次数和适应值下限值),则返回步骤(2);否则,退出算法,得到最优解。
2 卡尔曼滤波算法
卡尔曼滤波是以最小均方误差为准则的最佳线性估计,它根据前一个估计值和最近一个观测数据来估计信号的当前值,利用状态方程和递推方法进行估计,而且得到的解也是以估计值的形式给出的,最大的特点是能够去除测量系统中的随机误差,来获取更接近真实值的信息,能较好的应用于处理多变量系统,时变系统及非线性系统的最佳滤波等。卡尔曼滤波器结构[4]如图1。
对于离散域线性系统[4]:

式中x(k)是系统的n维状态向量;yv是m维带有噪声的测量向量;A是 n×n维非奇异状态一步转移矩阵;矩阵B是n×l维可选的控制输入u∈Rl的增益;C是m×n维观测矩阵。系统的n维过程激励噪声w(k)和m维测量噪声v(k)是不相关的零均值高斯白噪声。
离散卡尔曼滤波器递推算法为:


图1 卡尔曼滤波结构图
误差的协方差为:errcov(v(k))=CP(k)CT
3 基于粒子群算法和卡尔曼滤波器的PID控制
基于粒子群算法和卡尔曼滤波的PID控制系统结构如图2所示。
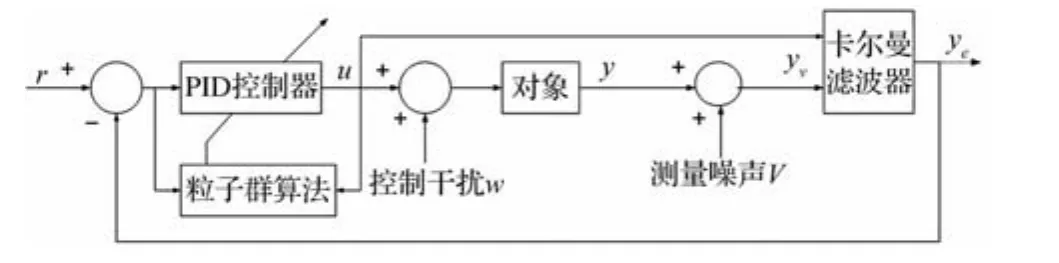
图2 与粒子群优化算法和卡尔曼滤波相结合的PID系统结构
控制系统通过卡尔曼滤波器对混有控制干扰信号和测量噪声信号进行滤波,反馈到系统输入端,利用粒子群算法对PID控制器的参数进行优化。
图2中粒子群算法与PID控制系统之间连接的桥梁是粒子(即PID控制器参数)和该粒子对应的适应值(即控制系统的性能指标)。优化过程如下:PSO产生粒子群(可以是初始化粒子群,也可以是更新后的粒子群),将该粒子群中的粒子依次赋值给PID控制器的参数Kp,Ki,Kd,然后运行控制系统模型,得到该组参数对应的性能指标,该性能指标传递到PSO中作为该粒子的适应值,最后判断是否可以退出算法。
4 仿真实例
设被控对象为系统[5]:

设采样时间为0.001 s,将传递函数进行离散化得到:

4.1 参数设定及仿真
假设系统的初值[6]x(0)=,u(0)=0,D=[0],P(0)=BQBT,取 Q=1,R=1。输入信号为一阶跃信号,控制干扰信号w(k)和测量噪声信号V(k)幅值均为0.002的白噪声信号,采用卡尔曼滤波器实现信号滤波。粒子群算法中的参数为:惯性因子w=0.6,加速常数c1=c2=2,维数为3(有3 个待优化参数 kp,ki,kd),粒子群规模为30,待优化函数为:
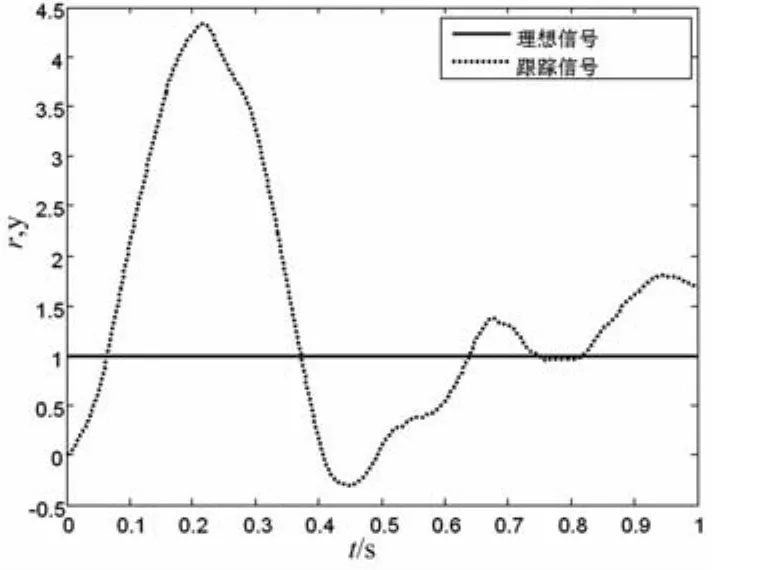
图3 常规PID控制阶跃响应

最大迭代次数为100,最小适应值为0.1,速 度 范 围 为[-1,1],3 个待优化参数 kp,ki,kd范围均为[0,10]。
(1)取kp=6.0,ki=0.8,kd=0.2(经验值),则常规的PID控制下系统的仿真结果如图3所示。
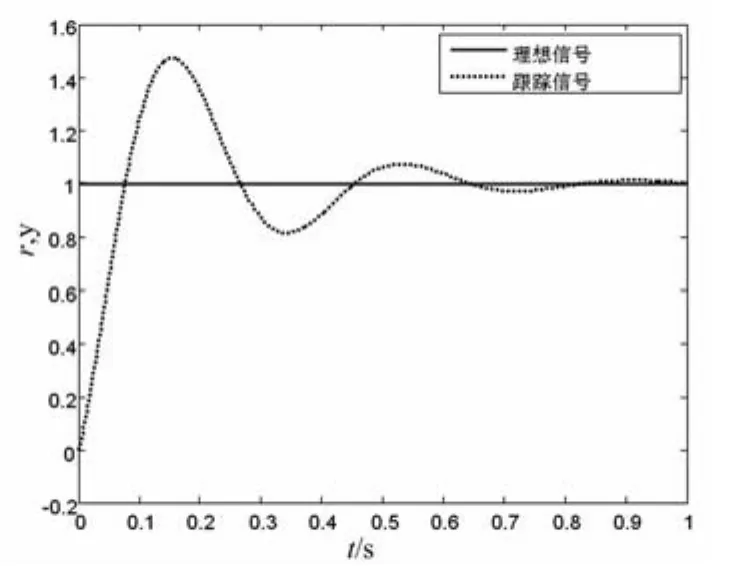
图4 基于卡尔曼滤波的PID阶跃响应

图5 仿真结果比较图
图中 r,y为无因次量,其中y为实际值,r为阶跃值,且r=1。横轴为时间轴,单位为 s;纵轴为数值轴,以下(图4及图6)相同。
(2)基于 R.E Kalman-PID控制系统的仿真结果如下图4。
(3)经粒子群算法优化后得到的参数为kp=9.307 1;ki=9.680 8;kd=0.477 0。基于 R.E Kalman-PSO-PID 的系统仿真结果与基于R.E Kalman-PID的系统仿真结果比较如图5所示。
4.2 仿真结果分析
比较图3与图4,可以看出,采用卡尔曼滤波的PID控制,可以得到稳定的系统输出,能够显著地减小噪声的影响。图5表明经粒子群优化算法和卡尔曼滤波算法的PID控制除了能够效抑制噪声对系统稳定性造成的不利影响外,还能够能够有效减少系统的峰值时间,减小震荡次数和超调量,使系统快速达到稳定状态,提高的系统的动态性能和静态性能,增强的系统的鲁棒性。另外,在利用粒子群算法对参数进行优化时,如果将搜索范围扩大到[0,300],我们得到另一组优化参数:kp=166.258 4,ki=294.035 1,kd=1.242 8,可以进一步提高控制器的控制品质,使上升时间更短,且使系统进入的稳态时间缩短了约50%,快速达到目标值,仿真结果如图6。
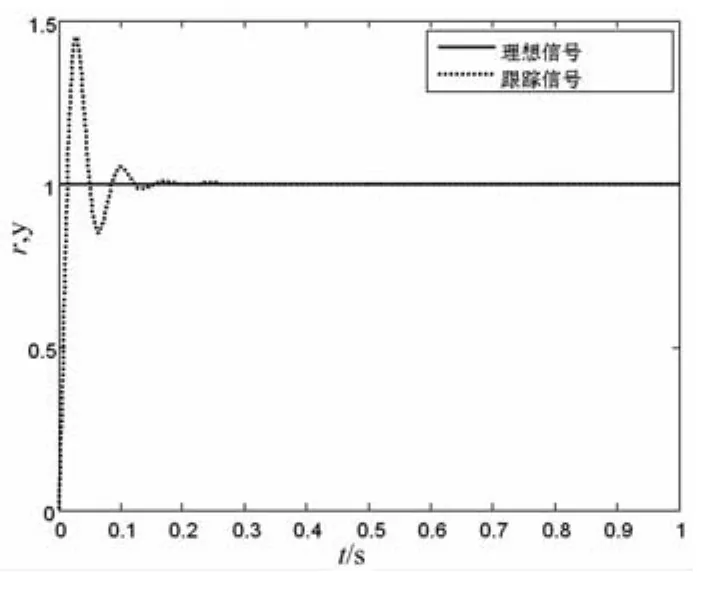
图6 参数优化系统仿真曲线
5 结束语
本文提出基于粒子群算法和卡尔曼滤波器的PID控制方法,有效地解决了PID控制系统中参数的整定以及控制干扰信号和测量噪声信号问题,提高了系统的抗干扰能力和控制品质。仿真结果表明这种控制方法能使系统各项指标有了明显的提高,尤其是超调量有了明显的减少,缩短上升时间。该方法有一定的实用价值。
[1]史峰,王辉,胡斐,等.MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2012:130-131.
[2]许国根 ,贾瑛.模式识别与智能计算的MATLAB实现[M].北京:北京航空航天大学出版社,2012:211-212.
[3]杨淑莹.模式识别与智能计算——MATLAB技术实现[M].北京:电子工业出版社,2011:345-347..
[4]刘金琨.先进PID控制MATLAB仿真[M].北京:电子工业出版社,2011:64-65.
[5]胖永新,金迪,孟宪东.球杆系统的建模、仿真与控制器设计[J].武汉大学学报(工学版),2005,38(6):142 -146.
[6]谢新月,廉凤慧,于亦凡.卡尔曼滤波器在PID控制器中的应用研究[J].工程与试验,2009,49(3):16-18.
