一种镜像频率抑制方法研究

雷霖，罗浚溢，田书林

（1.成都大学 电子信息工程学院，四川 成都 610106;2电子科技大学 自动化工程学院，四川 成都 611731）

0 引言

对射频信号中的镜像频率进行有效抑制是中频接收机关键技术之一，在很大程度上是衡量中频接收机性能优越性的相关指标［1］。传统上使用最多的方法是超外差式［2］，这种方式的前端必须预先设置高频镜像抑制滤波器，这就必然要求中频fIE足够高，而且这种前置滤波器不能集成实现不利于在数字电路中运用。正交下变频镜像抑制方法克服了超外差式的缺点，这种方法最大的优点是不需要前端高频镜像抑制滤波器，易于集成实现。在理想情况下，正交下变频具有完全的镜像抑制能力，可以简化射频前端，使接收机的设计更加方便，但是正交下变频需要IQ两个支路完全同步，由于使用了非理想的混频器、滤波器、自动增益控制模块等等器件将造成两个支路的相位与增益失真，影响了镜像信号的抑制能力［3］。随着软件无线电技术［4］的发展使得ADC可以最大限度地直接接近射频天线，使所有的处理过程都在数字域实现，有效地减少了由于器件原因所造成的误差。周期非均匀采样［5］可以在没有前置镜像抑制滤波器和正交混频器的情况下把射频信号下变频到基带或者低中频，使用广义逆就可以直接得到抑制镜像频率之后的信号，将复杂的I/Q不平衡问题转化为矩阵向量方式，这样可以简化对系统的校正方式。

本文首先建立了直接交替采样抑制镜像频率的模型，利用时间交替采样的时间延迟为采样信号的中心频率的四分之一时对镜像频率有最大抑制效果的特点［6－7］，借助联合子空间理论把镜像频率抑制的过程转换为矩阵向量运算，并对通道失配的误差进行了有效补偿，最后的实验证明了本文提出的方法可以有效地实现镜像频率的抑制。

1 镜像抑制方法

假设信号x（t）∈L2为N个频带组成的严格带限带通信号，每个频带的带宽不超过B，频率范围－fn≤f≤fn其频谱分布如图1所示。

两通道周期非均匀采样镜像抑制系统如图2所示。

图1x（t）频谱图

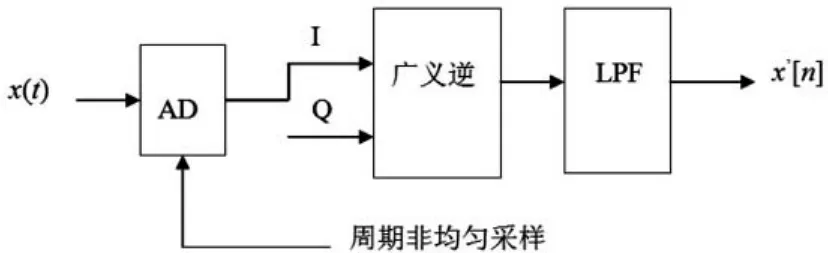
图2 周期非均匀采样镜频抑制结构图

定义2路非均匀采样序列对信号进行采样，使原始输入射频信号x（t）分为I、Q两通道，第一路与第二路之间时间差τ=的采样时钟的ADC进行采样，其中fc为信号中心频率。则相位差为:Δθ= －2πfcτ，表示在中心频率 ±fc处相位差为∓90°。

则两通道采样序列为:

式中T为采样周期，τ为采样序列时间间隔则采样后的序列yi（t）为:

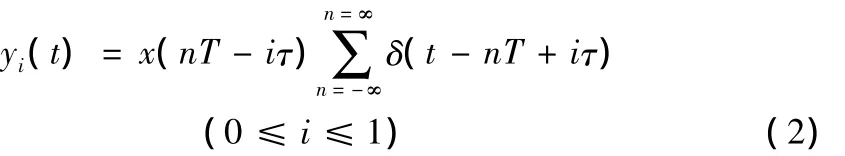
其中y0（t）、y1（t）分别为I、Q通道采样后的序列。

对yi（t）做Fourier变换得:

为了能从采样点Yi（ω）中得到抑制后的信号x（t），设x（t）位于L2子空间V（φ）。

令W（t）=［φ0（t），φ1（t）］T为 2阶生成函数，定义空间V（φ）:

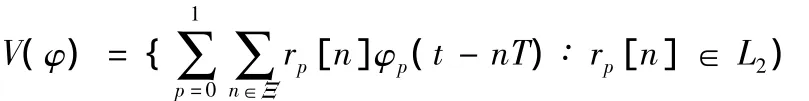
式中T为采样周期，φ（t）为空间生成函数，

对于任意x（t）∈V（φ）有:

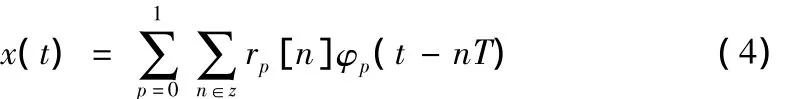
为了使任何信号x（t）满足x（t）∈V（φ）都可以用rp［n］表示，φp（t－nT）必须构成子空间V（φ）的一个Riesz基，即存在严格定义的两个正常数A＞0和B＜∞，使得:

上述子空间V（φ）为单一空间中，实际的抑制过程却是在联合子空间中进行的，为了能更好的对镜像频率进行抑制，定义一个联合子空间∪Vp（φ）:

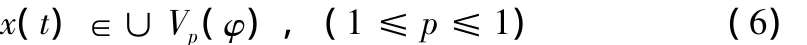
对于联合子空间理论，其目的就是为了能够得到抑制后r［n］的值。对（4）式做Fourier变换得:

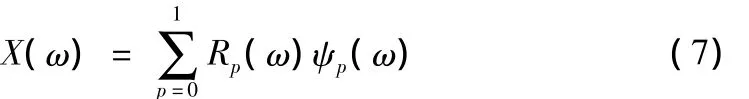
式中Rp（ω）为rp［n］的离散 Fourier变换，ψp（ω）是 ψp（t）的连续Fourier变换。

把式（11）代入式（3）可得:

由于只是两通道采样系统且信号对称分布在正负频率区域内，则式（8）和式（9）可化简为:

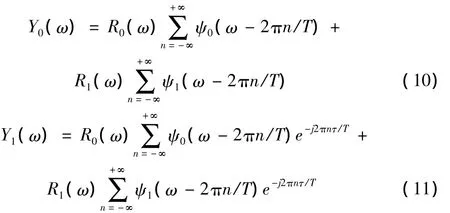
式中，R0（ω）、R1（ω）分别表示信号在负频率部分和正频率部分的频谱。

联立（14）和式（15）可得方程组:

改写成矩阵形式为:

方程（13）的广义逆可以通过正则法、最小二乘算法求得，这里不再做详细说明。因此可以定义H（ω）的Penrose广义逆。

式中:（·）H为转置共轭。

由此可以求出（13）的解:

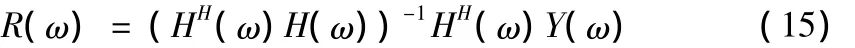
则可以得到:

式中X'（ω）为重构信号x'［n］的离散傅里叶变换，这里R0（ω）、R1（ω）为基带信号。X（ω）为基带信号，此时周期非均匀采样同时实现了镜像频率抑制和下变频。

2 误差补偿

由于AD的时间抖动必然会造成I、Q两通道的失配，仅仅采用上述的镜像频率抑制方法是不够的，必须要对误差进行补偿，补偿结构如图3所示。使用一个固定的滤波器C（ω）连同X'（ω）的复共轭函数作为基准信号，X'（ω）与该基准信号之差即为最终所求的（ω）。

图3 误差补偿系统

假设射频信号x（t）是由基带信号经过频谱搬移得到。

设与射频信号x（t）一致的无失真基带信号的时域表达式为z（t），令z（t）=zI（t）+jzQ（t），则有:

式中，（）*为共轭

则可以得到:

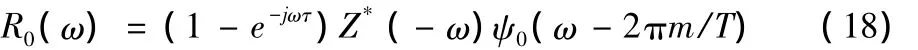
式中m表示负频率部分平移到搬移的基带的次数，Z*（－ω）为z*（t）对应的离散值的傅里叶变换。则有:

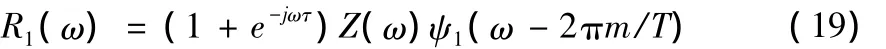
式中m表示正频率部分平移到搬移的基带的次数，Z（ω）为z（t）对应的离散值的傅里叶变换。

则式（16）可改写为:

则可以得到修正后的信号（ω）:

式中G1（ω）和G2（ω）分别表示Z（ω）和Z*（－ω）的增益。

从式（21）中不难看出，当镜像频率Z*（－ω）的增益为零时，系统有最大的抑制效果，即有:

3 实验与分析

设多带带通信号的原始频谱图如图4所示，带宽为360 MHz，中心频率为580 MHz，令采样频率1/T=360 MHz，时间延迟τ=，定义空间生成函数为:

本文使用FIR滤波器逼近补偿函数C（ω），这里选用3型FIR滤波器，其表达式由式（28）所示:

式中M表示的是滤波器的阶数。

图4 输入信号原始频谱图

本文选择八阶滤波器实现系统的镜像抑制，最大可实现－110 dB的衰减，其衰减效果如图5所示。

图6所示的是传统镜像抑制方法对信号的抑制效果，从图中不难看出传统的下变频最大衰减为－90 dB。

图5 系统抑制效果

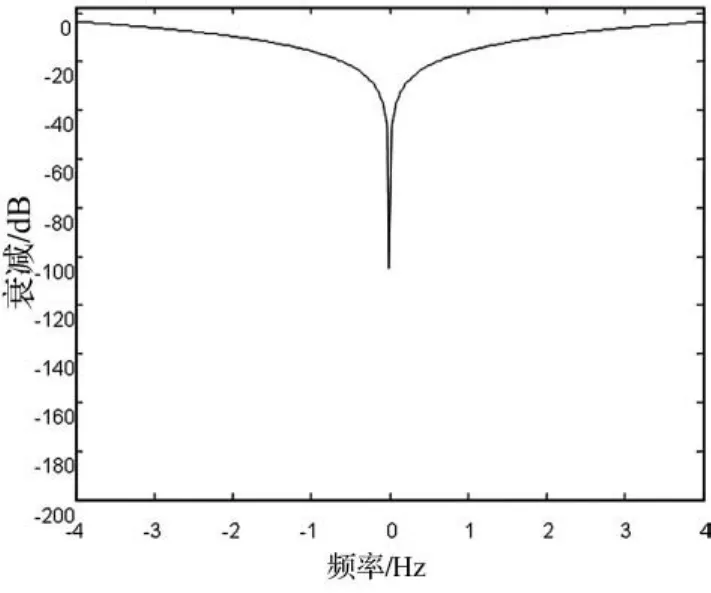
图6 传统方式抑制效果

图7表示的是经过时间交替采样后负频率部分被抑制，图8表示的经过求解广义逆之后的X'（ω）频谱图，比较图8与图4可知信号失真严重，这是由于两通道间存在着通道失配误差。图9表示的是经过补偿系统之后的信号频谱图，比较图9与图8，图9克服了图8中的失真现象;比较图9与图 4，最终输出结果表明系统实现了多带带通信号的下变频与镜像抑制。

图7 延时操作后的信号频谱图

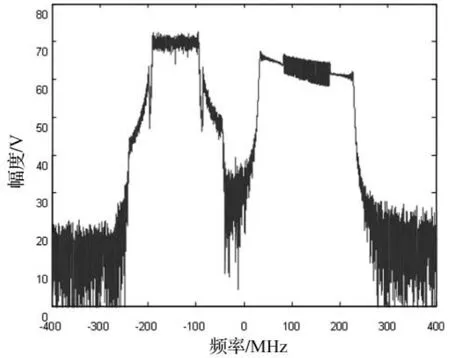
图8 未经补偿操作的信号频谱图

图9 系统最终输出频谱图

4 结束语

针对实际采样中往往有对镜像频率进行抑制的需要，本文提出了一种基于广义逆的镜像频率抑制系统，利用周期非均匀采样的时间延迟为采样信号的中心频率的四分之一时对镜像频率有最大抑制效果的特点，借助联合子空间理论把镜像频率抑制的过程转换为矩阵向量运算，通过广义逆就可以得到抑制的信号;针对由于通道失配造成的系统误差，提出了一种前向固定式误差补偿方式;并与传统的镜像抑制方式进行了比较得出了本文提出的方法在抑制效果等方面都好于传统方式。

［1］向新.软件无线电原理与技术［M］.西安:西安电子科技大学出版社.2008.

［2］ Stephen A.Jantzi，quadrature bandpass delta-sigma modulation for digital radio［J］，IEEE journal of solid-state circuit，1997，32（12）;1935－1950.

［3］ Supisa Lerstaveesin，A Complex Image Rejection Circuit With Sign Detection Only［J］，IEEE journal of solid-state circuits，2006，41（12）:2693－2702.

［4］ Junghwa Bae and Jinwoo Park，An Efficient Algorithm for Band-pass Sampling of Multiple RF Signals［J］.IEEE signal processing letters，2006，13（4）:193－196.

［5］罗浚溢;田书林;王志刚.稀疏信号的周期非均匀采样［J］.计量学报，2012，4（2）:111－118.

［6］ Feixue W，Shaowei Y，Guirong G.Mixer-free digital quadrature demodulation based on second-order sampling ［J］.Electron.Lett.，1998，34:854－855.

［7］ Coulson A J，Vaughan R G，Poletti M A.Frequency shifting using bandpass sampling.IEEE Trans.Signal Processing，1994，42:1556－1559.