基于EMD的次同步扭振模态参数的普罗尼分析

姜建国，刘凡齐，战祥建

（1.东北石油大学 电气信息工程学院，黑龙江 大庆 163318;2.大庆油田有限责任公司电力集团供电公司，黑龙江 大庆 163318）

0 引言

次同步扭振［1］是影响电网稳定性的主要问题之一。本文提出基于EMD优化小扰动模态参数的普罗尼辨识法，把EMD的时空滤波特征与小扰动测试信号的频率特征相结合提取小干扰分量，通过普罗尼［2］算法辨识其模态参数，利用重采样处理提高参数辨识精度。

1 基于EMD的分量提取与重采样处理

通过EMD提取次同步扭振分量［3－4］如下:

（1）使所有次同步扭振模态分量合成一个统一的扭振分量，忽略高、低频分量。对信号的各个分量进行频谱分析，如果某分量的次同步扭振频率范围内的频谱小于次同步扭振模态分量的频谱，则忽略掉该分量，否则保留分量并合成。

（2）经过频率筛选的次同步扭振模态分量可能包含噪声频谱，再对信号进行阈值处理。阈值去噪处理的模型及阈值计算如下:

在模态参数的普罗尼辨识［5］时，采样频率过高会导致辨识的精准度下降。所以，低频振荡普罗尼分析时，频率一般取20 Hz。在实际工况中，采样频率应大于信号最高频率的两倍，次同步扭振分析，采样频率应大于100 Hz。适当降低采样频率，可以提高频率分辨力即可改善普罗尼算法的精准度［6］。

次同步扭振模态参数辨识中另一关键是数据窗的选择。数据窗过窄使数据信息缺失，使分析结果误差过大;数据窗过宽增加计算的繁冗度，对阻尼参数较大的模态分量，导致无法辨识模态参数。数据窗的长度应大于次同步扭振信号中最低频率周期的两倍。

2 次同步扭振模态参数普罗尼辨识

经重采样处理和经验模态分解提取后，进行普罗尼分析，得到各次同步扭振模态的频率、衰减因子、幅值和相位，对精度有多方面的改进。基于EMD和普罗尼算法的次同步扭振模态参数辨识［7－9］流程如图 1 所示。

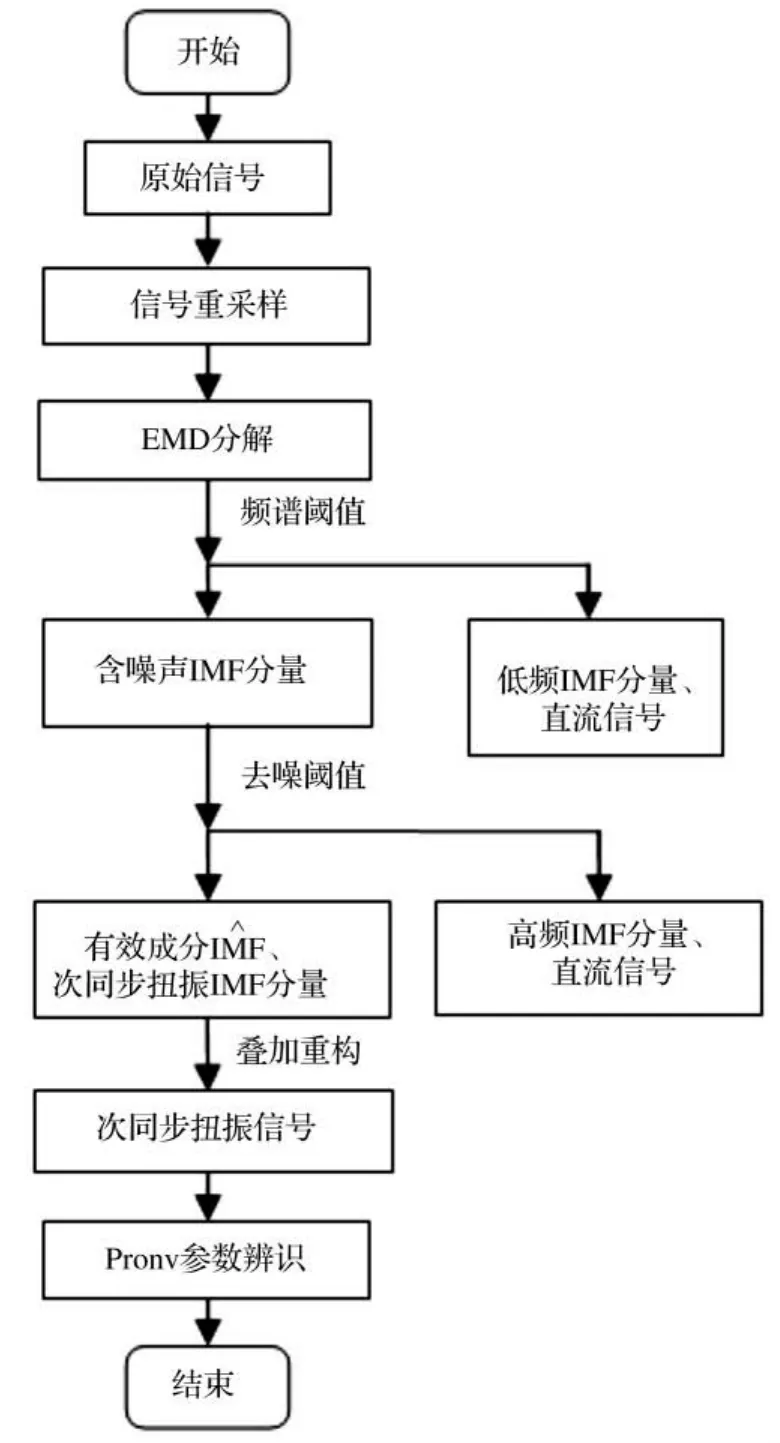
图1 基于EMD的次同步扭振模态参数Prony辨识流程图

给定测试信号:

包含三个次同步频率、低频、工频、二倍工频分量各一个，采样频率400 Hz，数据窗0～16 s，做普罗尼分析。在x1（t）中加入幅值为0.5的直流分量x2（t）:

对信号x2（t）进行普罗尼分析，结果比对如表1所示。可知对不含噪声信号而言，普罗尼算法分析精确度较高，直流分量信号的加入对普罗尼分析结果存在影响。

在待测信号x1（t）上，添加方差为1的噪声信号:

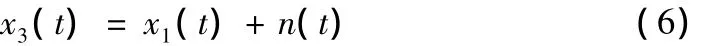
采用本文方法对测试信号x3（t）进行普罗尼分析验证。结果如表2，给出了三种数据窗的分析结果，可得数据窗长度对结果有影响。

由图1中结果可知，辨识结果准确度受采样频率和数据窗的影响，当噪声较高的情况下，衰减系数较大的分量受到的影响更大，所以对信号重采样处理时采样频率和数据窗的选择很重要。对次同步扭振而言，重采样的采样频率在150～500 Hz、数据窗在8 s时的准确度最好。

以上文结论为理论依据，对测试信号x3（t）分别用方法1:三阶Butter-worth带通滤波处理;方法2:小波滤波处理;方法3:EMD滤波处理进行滤波。各滤波方法的普罗尼辨识结果如表3，图2为拟合信号和理想信号。

由表3得，由于滤波器参数选取适中，方法1的幅值、频率、衰减系数辨识效果较好，但相角辨识结果偏差过大;方法2的辨识结果与拟合效果一般;方法3虽然辨识结果一般，但拟合信号优质，能切实反映次同步扭振。

3 电厂扭振实例验证

对某电厂的实测负荷扭振的瞬时转速数据进行分析［10－11］，采用本文的方法3辨识其轴系扭振模态参数。已知机组次同步扭振模态频率计算值为:13.1 Hz，24.9 Hz，29.8 Hz。图 3 为电厂机头滤波数据曲线，原始数据的采样频率取20 kHz。

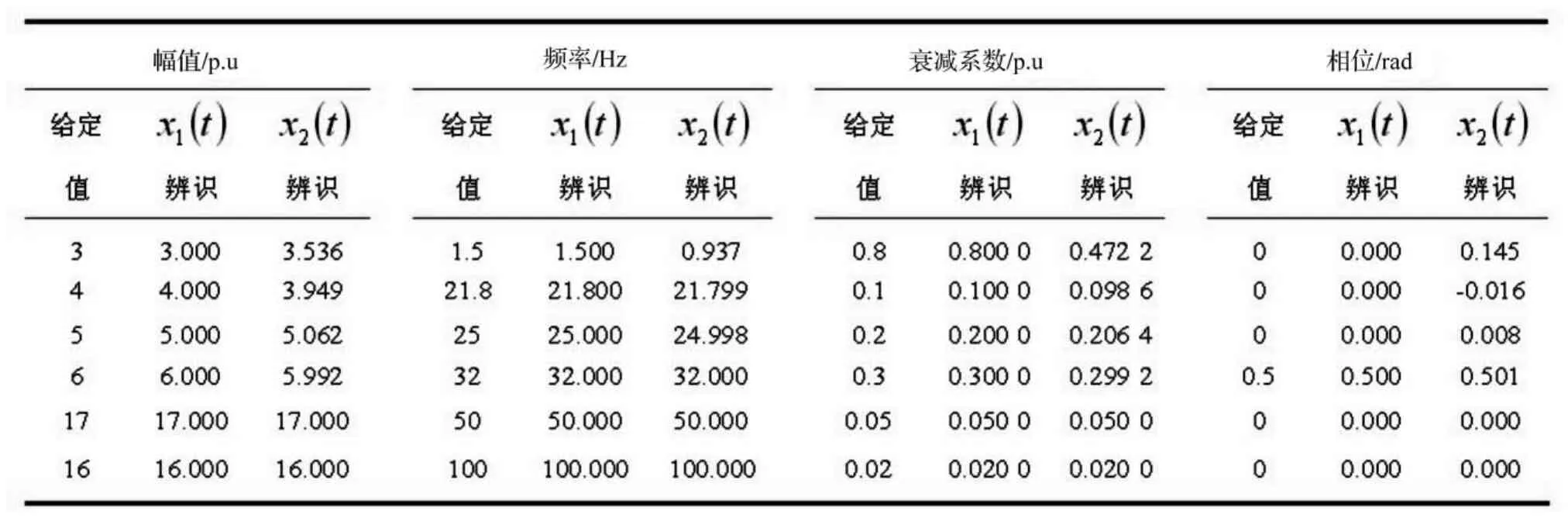
表1 测试信号x1（t）和x2（t）辨识结果

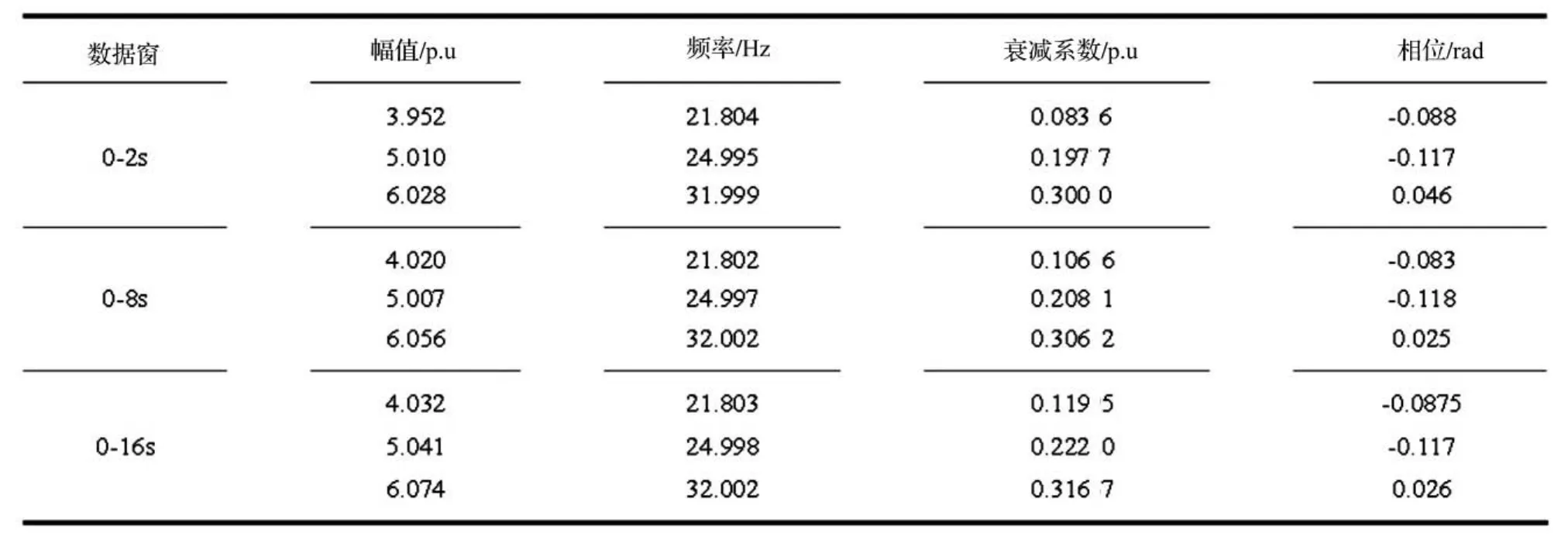
表2 不同数据窗的辨识结果

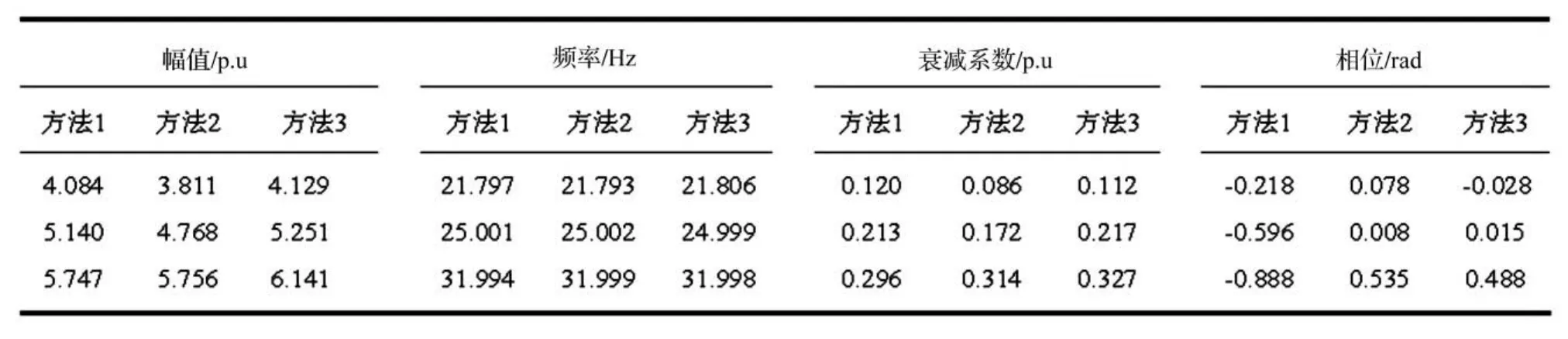
表3 含噪声信号的辨识结果

表4 转速实测数据的辨识结果

对原始信号通过滤波来剔除趋势项与噪声信号，再进行快速傅里叶变换，得图4的频谱图，得该滤波信号由频率为 13.0 Hz、24.9 Hz、29.5 Hz的次同步扭振模态组成。

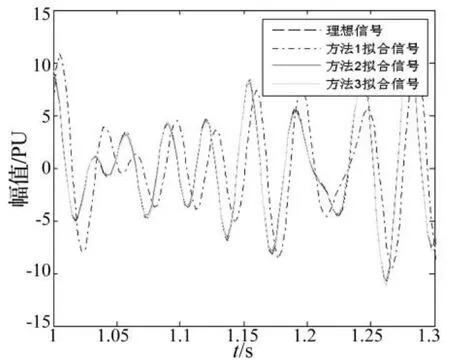
图2 三种滤波方法的Prony拟合信号

从图 3得，负荷激振发生的时间为 1.3 s，因为扰动初始暂态分量复杂，所以对原始信号的重采样应在扰动初始后，采样频率取400 Hz，由于数据窗的长度不能无限延展，故取数据窗宽度为1.5 s～4.5 s。对重采样信号分别进行三种滤波处理，对滤波所得数据进行普罗尼分析，结果如表4。

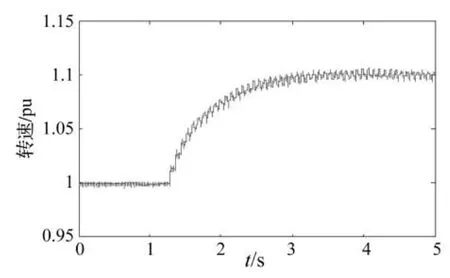
图3 转速录波数据曲线

由表4得，方法3的辨识结果的次同步扭振模态频率和计算值、傅里叶变换的分析结果相同，衰减系数位于经验值范围内。证明文中的方法3对次同步扭振模态参数的辨识是有效的。

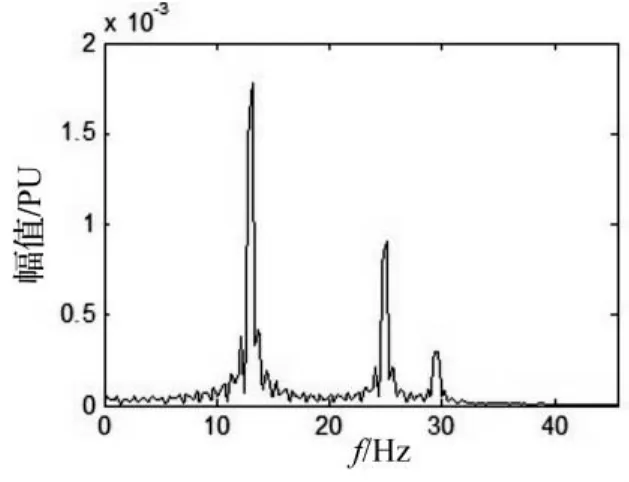
图4 快速傅里叶变换分析结果

4 结束语

本文以经验模态分解与普罗尼结合，对小扰动模态参数辨识，结论如下:

（1）由经验模态分解的时空滤波特征和扭振信号的频谱特征，合成唯一的次同步扭振分量可对噪声及其他频率的干扰信号有所抑制。

（2）对原始信号的重采样处理中合适的数据窗口的长度和采样频率可改善次同步扭振模态参数辨识精度。对次同步扭振而言，重采样的采样频率在150～500 Hz、数据窗在8 s左右时辨识精度最高。

（3）经过重采样处理和经验模态分解提取次同步扭振分量，再进行次同步扭振模态参数辨识的方法精准度较高。

［1］于达仁，鲍文，苏杰先.一种新型的次同步扭振测量方法［J］.电力系统自动化，2000，24（17）:1 －3.

［2］伍凌云，李兴源，孙衢，等.基于Prony辨识的复杂交直流系统次同步扭振特性分析［J］.四川大学学报（工程科学版），2008，40（3）:155－160.

［3］张少康，李兴源，王渝红.Prony算法在电力系统参数辨识中的应用［J］.电网技术，2010，34（7）:22 －24.

［4］侯王宾，刘天琪，李兴源.基于自适应神经模糊滤波的低频振荡Prony分析［J］.电网技术，2010，34（6）:53 －58.

［5］董航，刘涤尘，邹江峰.基于Prony算法的电力系统低频振荡分析［J］.高电压技术，2006，32（6）:97 －100.

［6］赵礼杰.基于EMD的Prony算法在低频振荡模态参数辨识中的应用［J］.电力系统保护与控制，2009，37（23）:9 －14，19.

［7］ Huang N E.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis［J］.Proc R Soc Lond A，1998，454:903－995.

［8］ Smith J R，Hauer J F，Trudnowski D J.Transfer function identification in power system applications［J］.IEEE Trans on Power Systems，1993，8（3）:1282－1290.

［9］郑蕤，肖湘宁，李伟，等.复杂交直流系统次同步扭振模态辨识及仿真验证［J］.高电压技术，2010，36（12）:3035 －3040.

［10］ First Benchmark Model For Computer Simulation Of Subsynchronous Resonance［J］ .IEEE Transactions on Power Apparatus and Systems，1977，96（5）:645 －672.

［11］郝志勇，付鲁华.汽轮发电机组转子轴系扭振系统部分模态施控特性研究［J］.控制理论与应用，2002，19（1）:95－98.