过饱和路口交通信号设计:经典模型及最新方法的比较与总结

陈帅宇，徐 浩，刘鸿潮*

(1.沃尔特穆尔和联营公司，得克萨斯州休斯顿，美国;2.得克萨斯理工大学土木与环境工程系，得克萨斯州拉伯克市，美国)

1 Introduction

More and more urban signalized intersections in theUnited States are operating in saturated or oversaturated conditionsduring the morning and afternoon peak hours. Unlike undersaturated intersections，for which many well-established theories and signal timing policies have been developed，consensus has not been reached with regard to the control philosophy and timing strategy of oversaturated signals.The majority of the traffic signals in the United States are timed by a handful of signal timing software packages(e.g.，Synchro，TRANSYT-7F and PASSER).How to improve their performance on timing oversaturated intersections is of significant importance to traffic engineers given the frequency of oversaturated conditions.

For an isolated oversaturated intersection，timely and efficient allocation of green time among the intersection approaches is essential to optimize traffic flows.Mathematical models on signal timing variables for oversaturated intersections have been proposed by a number of researchers.A couple of the studies were focused on the green timeallocation or phase switching policy and have resulted in reasonable control policies that could possibly be implemented.However，the implementation has not been seen in the field due in part to the fact that most of the models have never been evaluated.

Gazis and Potts［1］first revealed that the total intersection delay would be minimized if the queues on all(critical)approaches could be dissolved simultaneously.Gazis［2］further verified the concept by using an example of an oversaturated intersection of two one-way streets.Based on this principle，Michalopoulos and Stephnopolos proposed their socalled“bang-bang”two stage signal control model［3］in which a constraint on queue length was considered.Recent studies along this route include research of Chang and Lin［4，5］，who proposed a discrete dynamic model and performance index approach to optimize signalparameters during the entire period of oversaturation.In the research of Yin，focuses were placed on investigating the effect of fluctuation on optimal timing of fixed-time signals［6］.

Dans and Gazis［7］further stated that giving priority to the oversaturated approach with higher saturation flow rate would be beneficial to delay optimization. In the same literature，a linear programming(LP)model was developed based on the so-called store-and-forward phase switching principle.Recently，researchers also started investigating control policies for a system of oversaturated intersections.For example，Lieberman et al.［8］conducted a mixedinteger linear program approach to explore feasible control policies of oversaturated arterials.Lo and Chow［9］developed a dynamic intersection signal controloptimization method based on the celltransmission model.Recent works along this line also includes work of Wong et al.［10］

The focus of another approach，which is different from the control principle/policy oriented study，is to develop control algorithms that rely on advanced computation，such as genetic algorithms(GA)for optimal signal timing and queue management of oversaturated intersections［11–13］.Li and Prevedouros presented a hybrid optimization and rule-based oversaturated control algorithm for adaptive signals［14］.The GA based approach seeks global optimum through the adaptive heuristic searching algorithm and does not necessarily rely on a clearly defined phase switching policy. A successful application ofthe GA based controlmodelis TRANSYT-7F.In the latest version，Hale introduced their methodology for timing oversaturated signals［15］.

Signal timing software packages have been widely used by traffic engineers and there are many advantages of using these readily available signal timing tools.However，the proprietary nature of the control algorithms embedded in those commercialized tools makes it difficult for in-depth investigation.On the other hand，the findings from theoretical models have not been used in practice to their full potential.This gap needs to be bridged for theory to remain relevant for practitioners.This in turn requires a thorough evaluation of the theoretical models and detailed comparison analyseswith regard to the performance of the theoretical approaches and the prevalent signal timing tools.

This paper examines two groups of classic models and compares their performance with two prevailing signal timing tools，TRANSYT-7F，V 10.3 and Synchro 7.The first group includes the graphical model，Pontryagin’s control model，and the discrete minimal delay model which belong to the bang-bang type of control and follow Gazis’simultaneous queue discharging principle;The second group includes the LP model which follows the principle of giving priority to oversaturated intersection approaches with maximum saturation flow rates;TRANSYT-7F was selected as a representative of the models whose green time allocation strategy is based on advanced formulation ratherthan a clearly defined phase switching policy;Synchro was selected to represent the models that assign green time according to the Highway Capacity Manual’s method［16］.The findings of this research may help researchers and practitioners in understanding theadvantages as well as the applicability and limitations ofthese theoretical models.Understanding of the control principles，in return，may play a positive role in improving the existing signal timing tools.

2 Background

2.1 Oversaturated conditions

A signalized intersection becomes oversaturated when traffic demand exceeds capacity，causing queues of vehicles to develop in one or all of the approaches ofthe intersection. The underlying assumption of the definition is that there is no effective green time loss at all intersection approaches during the oversaturated period.If one or more approacheshave effective green time loss，the intersection is said to be in pseudo-oversaturated condition because by adjusting the signal plan the intersection may be converted back to under-saturated condition.

The effective green time lossissometimes inevitable when traffic demand is reaching a certain threshold that a fluctuation has a reasonable chance of creating residual queues from one cycle to the next.Daganzo pointed out that such unpredictable stochastic fluctuations have little effect on the average delay if traffic is well under or well over saturation［17］.Throughout this paper，random delays caused by traffic fluctuation are not considered，only uniform delays are considered

Gazis and Potts［1］indicated that the sufficient condition for oversaturation at an intersection with a fixed time signal plan and constant cycle length C and lost time L per cycle is:

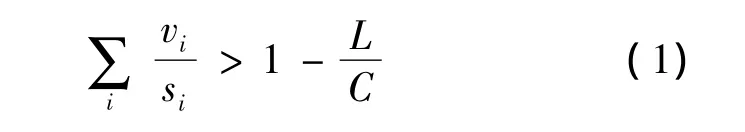
where viand siare the mean arrival rates and the saturation flow rates of the critical approach i of the intersection.

However，the current traffic condition is not only a result of current traffic arrivals and departures but also related to previous traffic conditions.At an oversaturated intersection，a certain amount of the effective green time must first serve the vehicles left during the previous cycle.In such a case，the steadystate condition breaks down and the signal timing task becomes more intricate than that for under-saturated conditions.Therefore the authors define the sufficient and necessary condition for oversaturation as:

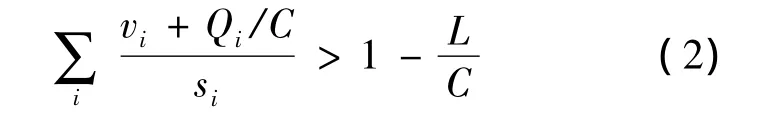
where Qiis the number of vehicles in the residual queues on the critical approach i of the intersection.

2.2 Control objectives and constraints

The most often used control objectives for signal timing design and evaluation are minimum total intersection delay and/or maximum throughput of the intersection.The objective of minimum intersection delay or average vehicle delay has been arguably the sole criterion for signal timing of under-saturated intersections as used by Webster［18］.If stochastic delay can be neglected，the goal becomes maximizing total throughput from the intersection subject to the following constraints:

(1)Queue length;(2)Maximum individual delay (Maximum individual waiting time);(3)Minimum green time.

For a theoretical model to be of practical value，these constraints must be considered.For example，the objective of minimizing intersection delay can be easily achieved (in the model)ifthere is no constraint on the queue length.However，it may cause an unfavorable situation in which queue may spill back and block the upstream intersection.The restrictions on the maximum individual delay and the minimum green time are equally important from the practical point of view.

2.3 Cumulative curve

A common objective for both fixed-time and realtime signal timing design is to develop traffic signal plans that minimize total vehicle delay，which can be achieved through the use of cumulative curves to represent(deterministic or uniform)traffic arrivals and departures.As shown in Fig.1，many theoretical models construct cumulative arrival and departure curves to illustrate the queue formation and dissipation process during the congested period.

If we label the first vehicle when the queue starts as vehicle number 1，and the last vehicle to arrive when the queue disappearsasnumber n，the shadowed area enclosed between A(t)and D(t)during the queuing time interval(t1，tn)represents the totalvehicle delay d during the period of congestion.

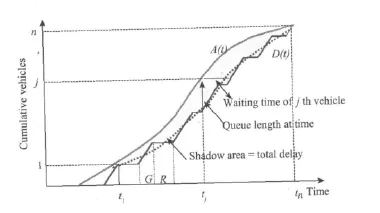
Fig.1 Cumulative curves at an oversaturated approach

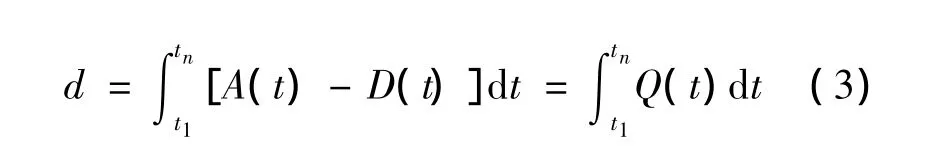
where A(t)represents the cumulative number of vehicle arrivals on the approach over time;D(t)represents the cumulative number of vehicle departuresattheintersection overtime;Q(t)represents the number of vehicles stored in queues.The horizontal distance between A(t)and D(t)represents the individual vehicle delay before it discharges from the intersection.This time-dependent definition is helpful in developing online and adaptive signal timing plans，in which accurate projection of real-time arrival is the key［19］.

If there are multiple lanes on one approach，in order to simplify the computation while maintaining the first-in-first-out(FIFO)criteria，one assumes that the queues are evenly distributed and no lanechanging behavior exists within the lanes.Delay of the approach is thus expressed by Eq.(4).

where dAis delay of the approach;dLis delay of single lane;a is the number of lanes on the approach.

Generally，departure curve D(t)is transferred to the smooth approximation，the dotted line shown in Fig.1.Hence，Eq.(5)shows the relationship between the queue length and the control variables.

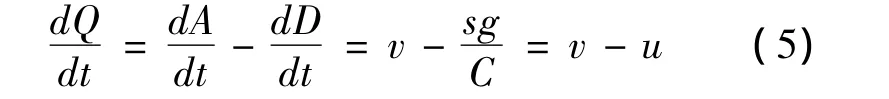
where v is the arrival flow rate;u is the departure flow rate;s is the saturation flow rate;g is effective green time;C is the cycle length.

2.4 Control algorithms of selected theoretical models

2.4.1 Graphical approach

Gazis and Potts first revealed that the intersection delay could be minimized if the queues on all(critical)intersection approaches are cleared simultaneously［1］. Based on this principle， the controlstrategy was developed by a graphical approach.giminand gimaxare the minimum and maximum effective green time of the approach i respectively;the associated minimum and maximum departure rates，i.e.，uiminand uimax，of approach i is:

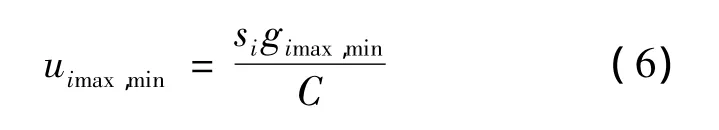
If S1＞S2，the conceptual two-stage operation process(bang-bang control)is illustrated by Fig.2.

Fig.2 Optimal control of graphical model

In the first stage，the departure rate of approach 1 is set to its maximum，u1max，the departure rate of approach 2 is set to its minimum，u2min;at the switch-over point τ，the second stage begins with the departure rate of approach 1 set to u1min，and the departure rate of approach 2 set to u2max.T is the termination time of the oversaturated period.Graphical model tends to search for the optimal switch-overpoint(τ)forminimalintersection delay.The solution is obtained by trial drawing and inspection.

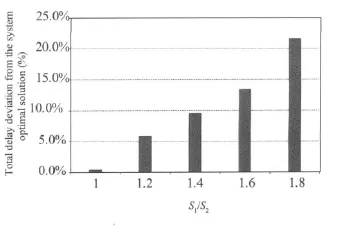
Fig.3 Total delay deviation under different saturation flow rates conditions

2.4.2 Pontryagin’s control model

Gazis［3］further developed his solution for oversaturated intersections by using Pontryagin’s maximum principle.Michalopoulos and Stephnopolos placed a constraint on the queue length into Gazis model and established a discrete algorithm based on the numerical method.For an intersection with two one-way approaches，the objective is to minimize the total queue length，which is:

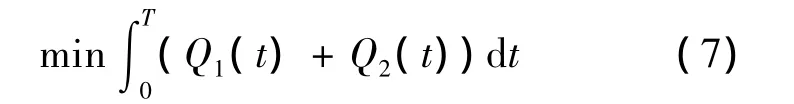
where Q1(t)and Q2(t)is the queue length of the first and second approach，respectively and

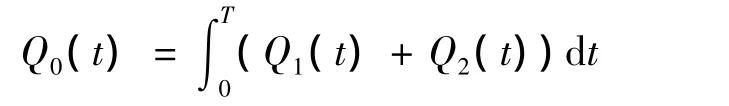
Steering functions f0，f1，f2were then defined for controlling the changes in the state variables:

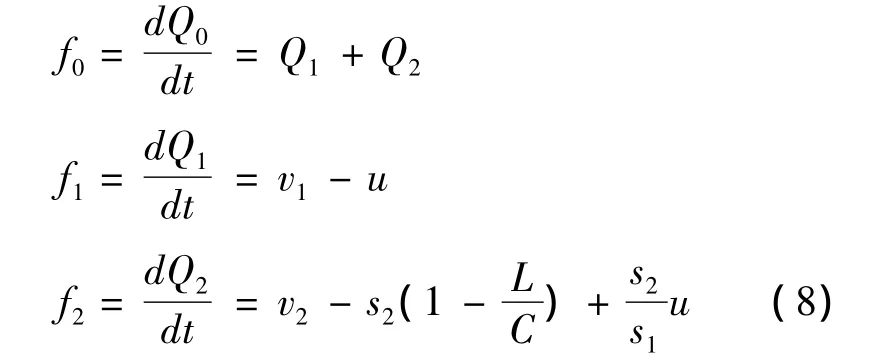
where u(the departure rate of the first approach)is a function of time and called control variable，v1，v2are the arrival flow rate for approach 1 and approach 2，respectively.The control domain is:

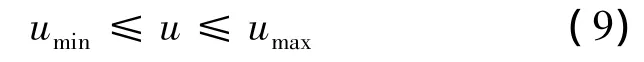
and the boundary conditions are:

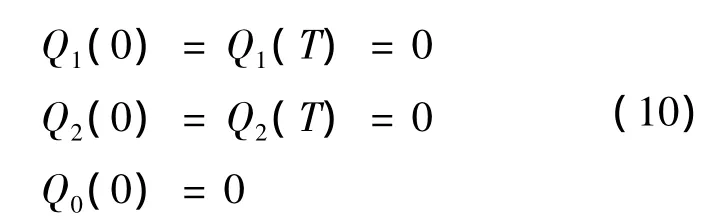
The solution follows the classicalPontryagin’s maximum principle. To implementPontryagin’s method one defines a Hamiltonian function:

where φ1，φ2and φ0are the functions of time.They are defined as follows:

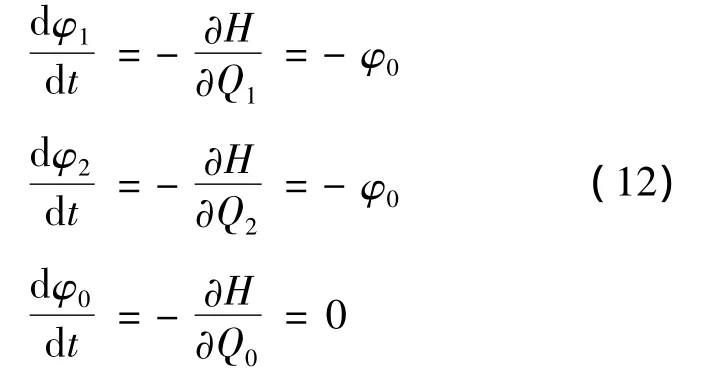
Therefore，

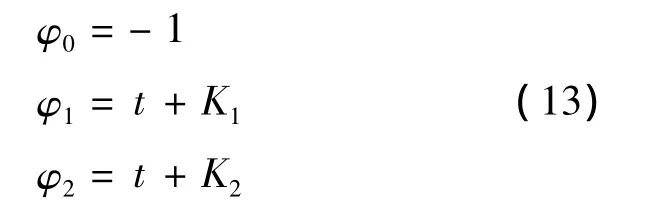
The optimum value of the control variable u at time t is the one that maximizes H.

Thus，the control algorithm reads:

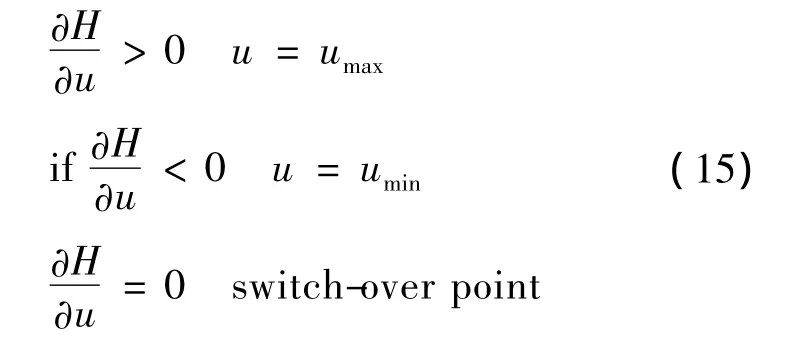
This model has provided the theoretical solution of Gazis and Potts’graphical model and has verified the bang-bang control［1］.

Michalopoulos and Stephnopolos further placed a queue length constraint into this model and drew the following conclusions:the optimalcontrolu is affected by the queue length constraint during finite time interval［3］. When queue length reaches its constraint，the departure rate must be equal to the arrival rate.If queues on both approaches reach the constraints and the cycle length is constant，the problem may have no feasible solution.

2.4.3 Discrete minimal delay model

Chang and Lin developed a discrete minimal delay model to solve the oversaturated problem［4］.Based on the delay model，a performance index model is also developed by introducing a penalty for the number of stops.In this paper，only their minimal delay model is considered.The objective function is to minimize total delay.The function is in quadratic form as below:

where N is the terminative state of the oversaturated period.

Based on the optimal control theory，the problem is to minimize the Hamiltonian function as follows:

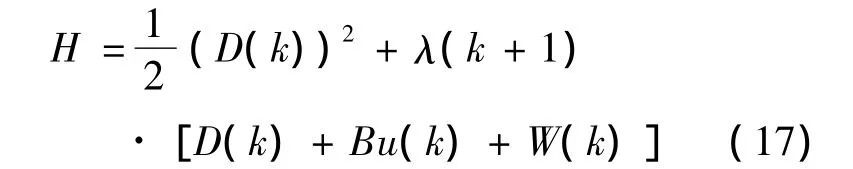
where λ(k+1)is Lagrange multiplier in state k+1 ，B is the control gain;u(k)is the control variable;W(k)is exogenous variable.

For the isolated intersection with two one-way approaches:

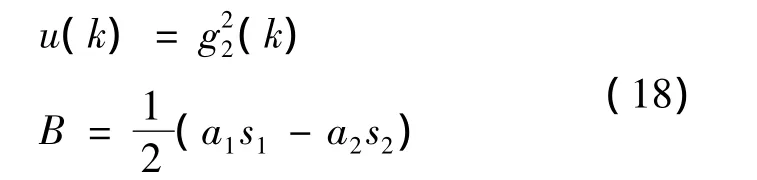
where g2(k)is the effective green time of approach 2 in the k th cycle;a1and a2are the number of lanes on approach 1 and approach 2，respectively;s1and s2are the saturation flow rate for approach 1 and approach 2，respectively.

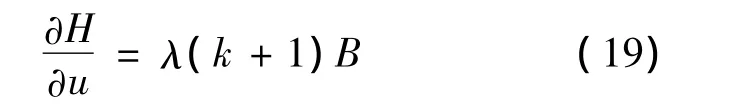
To minimize H，the control process is:

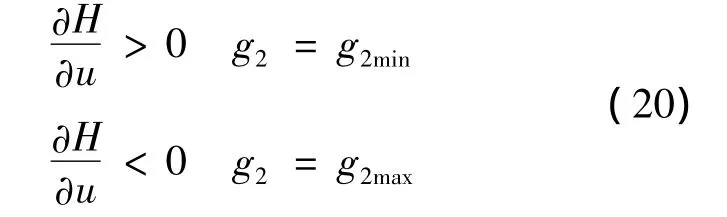
Clearly，it is a bang-bang type control with a twostage operation.The solution of this approach is consistent with the Pontryagin’s control model.

2.4.4 Linear programming(LP)model

Dans and Gazis proposed their LP model for a system of oversaturated intersections，in which the problem of an oversaturated intersection was further addressed［7］.The model was developed based on the concept that priority is given to the intersection approaches with higher saturation flow rates when green time is allocated among signal phases.The key for this approach is to keep the subject intersection approach saturated before switching to next green phase.The model reads:

where T is the duration of the oversaturated period

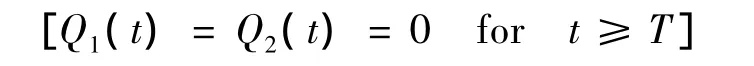
ConsiderN time intervals that N·Δt≥T and define:

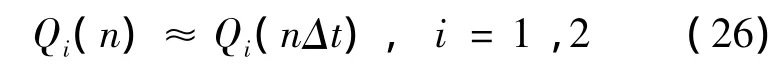
The objective function Eq.(21)becomes to:

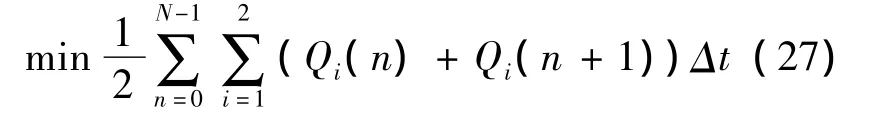
If one approximates the differential Eqs.(22)and(25)by difference equations，the problem becomes a standard LP problem.

As summarized in Table 1，the four classic models can be roughly classified into two groups by the patterns of queue dissipation.The first group includes the graphical model，Pontryagin’s control model，and the discrete minimal delay model which follow Gazis’simultaneous queue discharging principle. By applying differentoptimalcontrol methods，the models in this group lead to similar bang-bang type signalcontrolwith a two-stage operation.The second group includes the LP model which follows the principle of giving priority to oversaturated intersection approaches with maximum saturation flow rates.The effectiveness of these two groups of models are presented in the following section.

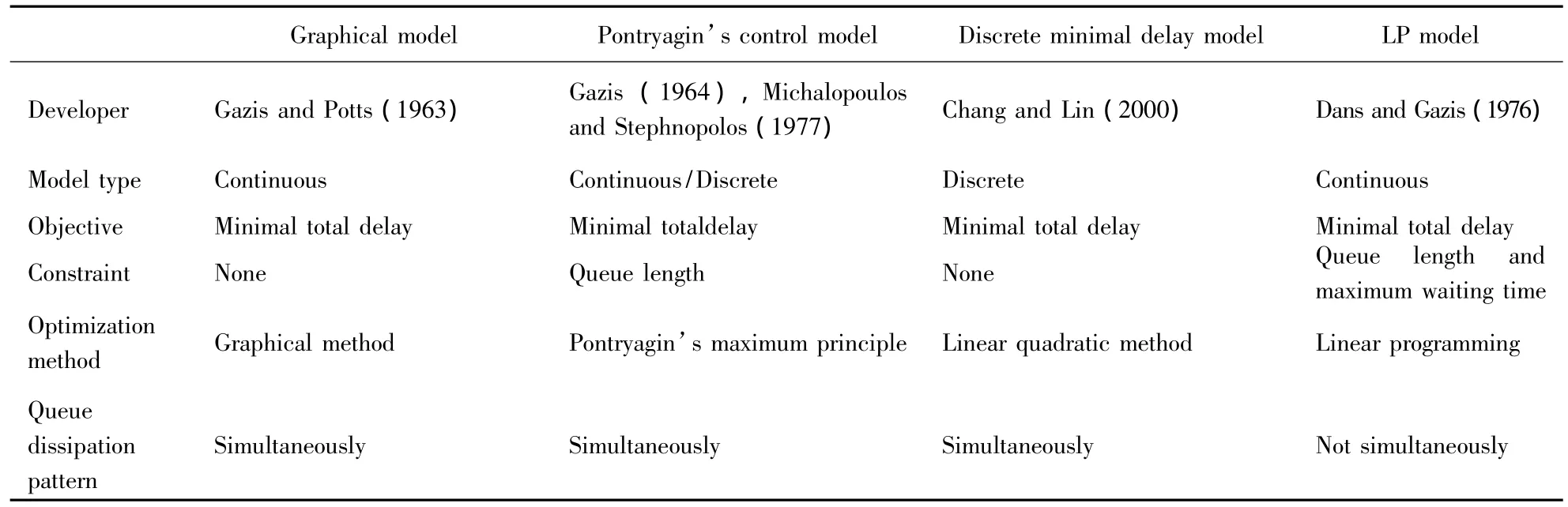
Table 1 Algorithms of theoretical oversaturated control models

3 Comparison analyses of theoretical models

3.1 Minimum effective green time

The minimum green time is usually governed either by the pedestrian crossing time or the time to allow one or two queued vehicles to pass through the intersection for actuated signals. From the mathematical point of view，the minimum effective green time is a boundary condition.As mentioned earlier，the regulation of minimal effective green time is treated as a constraint during the control process.A simplified case is now presented to show the relationship between the regulation and the control algorithm.

Note that all of the models are concerned with the phase switching policy issue，using a simplified case with two one-way approaches and two phases would be sufficient.The following example is similar to that used in Michalopoulos and Stephnopolos［20］.Consider an intersection with two one-way approaches with a two-phase signal control and the cycle length is 150 s(C=150).

Approach 1 has one lane and s1=1，400 pcu/h，g1max=0.65C(97.5 s)，g1min=0.4C(60 s);Approach 2 has one lane and s2=1，000 pcu/h，g2max=0.6C(90 s)，g2min=0.35C(52.5 s).Table 2 gives the five minute’s cumulative arrival volumes.

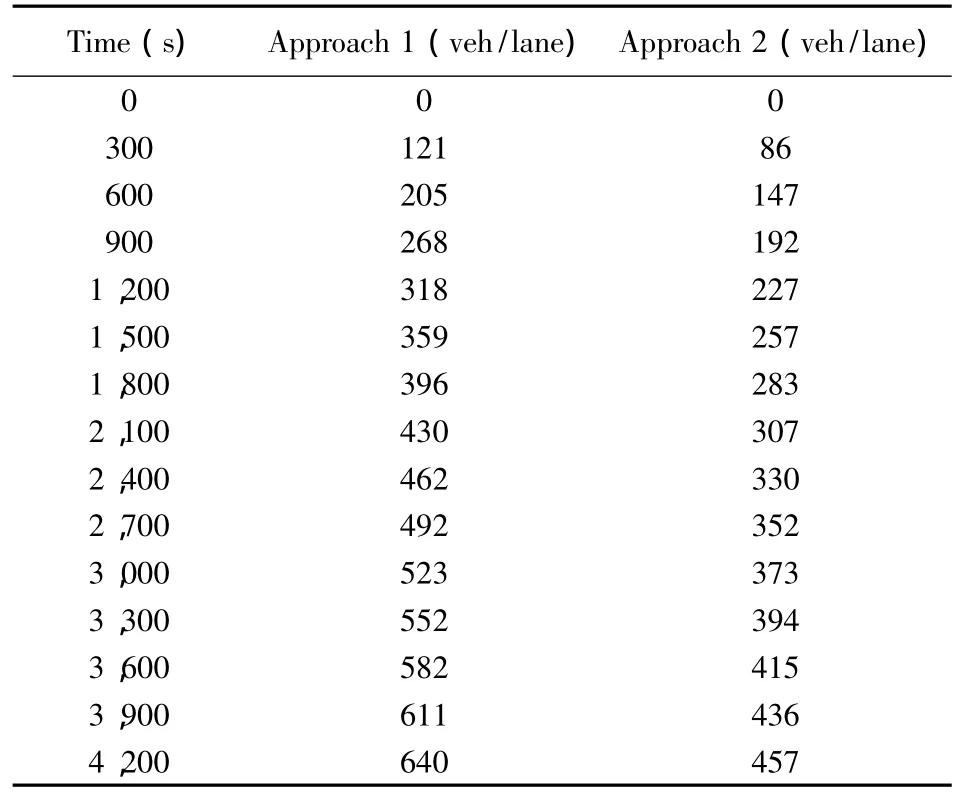
Table 2 Five-minute cumulative arrival volumes

According to Michalopoulos and Stephnopolos and Chang and Lin［3，4］，the optimal signal control scheme of the bang-bang control strategy is summarized in Table 3.The queues on both approaches are dissolved at roughly the same time(approach 1 at 2，100 s，approach 2 at 2，400 s).The switch-over point is at 1，050 s and the termination time is at 2，400 s.The total intersection delay summed from approaches 1 and 2 is 216，738 veh-s，which is equivalent to 124.78 s/veh in terms of average vehicle delay.The signal scheme for the same problem calculated by the LP model is shown in Table 4.

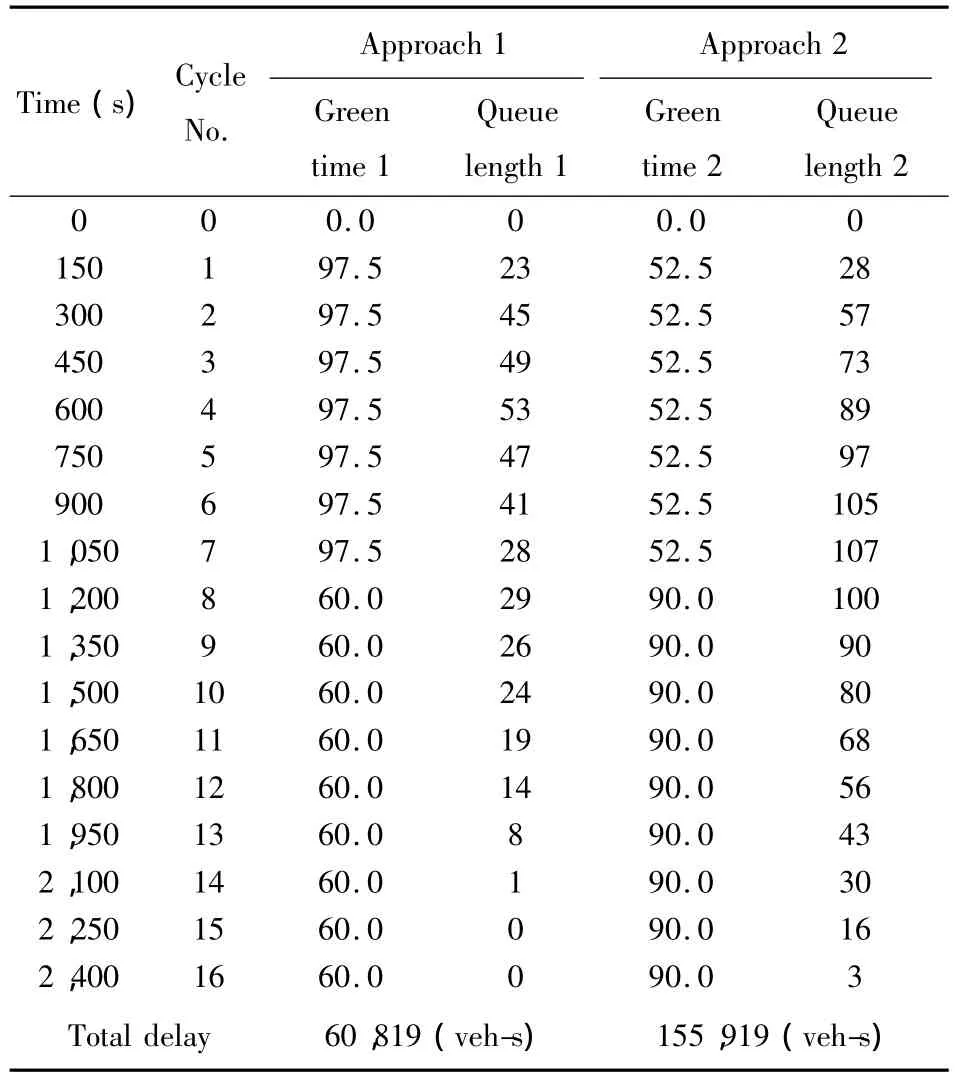
Table 3 Queue length and control strategy by bang-bang control strategy

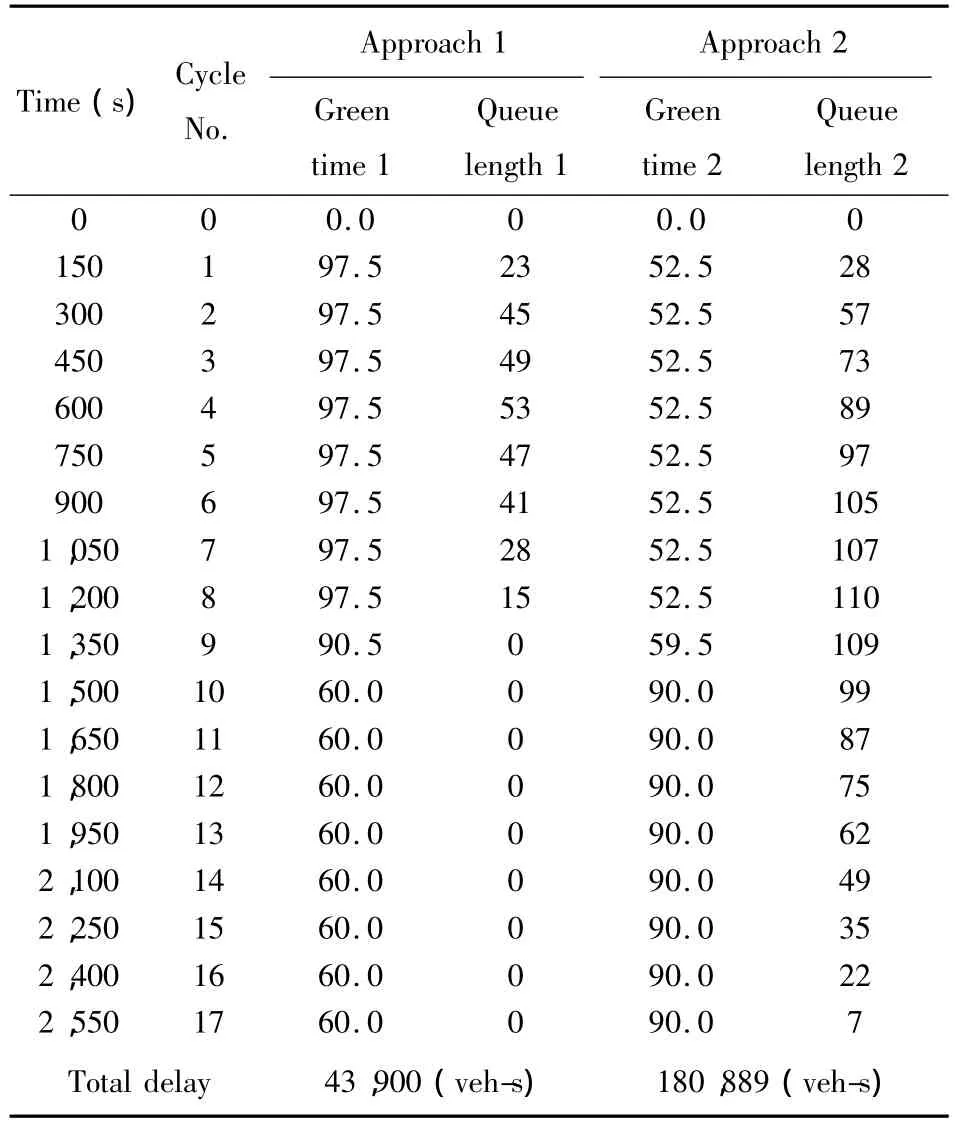
Table 4 Queue length and control strategy of the LP model

The queue on approach 1 dissipates at 1，200 s and the rest of the green time is then allocated to approach 2.The queue on approach 2 dissipates at 2，550 s. Totalintersection delay summed from approaches 1 and 2 is 224，789 veh-s，which is equivalent to 129.41 s/veh in average delay.

By comparing the results provided by these two types of models，it is revealed that the total delay calculated by the bang-bang control strategy is smaller than that of the LP model(216，738 ＜224，789).In the LP model，when the queue on the approach with maximum saturation flow rate is dissolved，the signal needs to be maintained at the saturation state.However，if the arrival rate is smaller than the minimal service rate on that approach，there is effective green time loss.In this example，the queue on approach 1 is dissolved at 1,200 s and queue on approach 2 isdissolved at 2,550 s. There is significant effective green time loss on approach 1 during［1,200 s，2,550 s］，which indicates that the intersection is in a pseudo-oversaturated condition.The constraint of minimal green time is shown in Eq.(28):

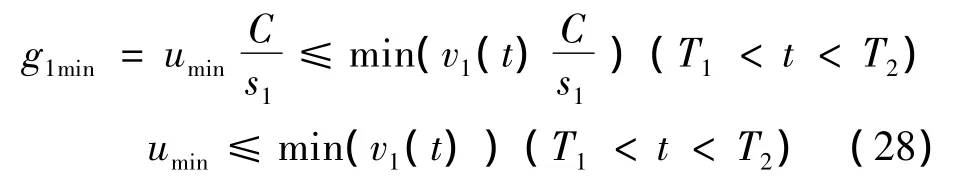
where T1and T2are the queue duration time of approach 1 and 2，respectively.

It is easy to verify that in bang-bang control，the control variable uminmust follow:

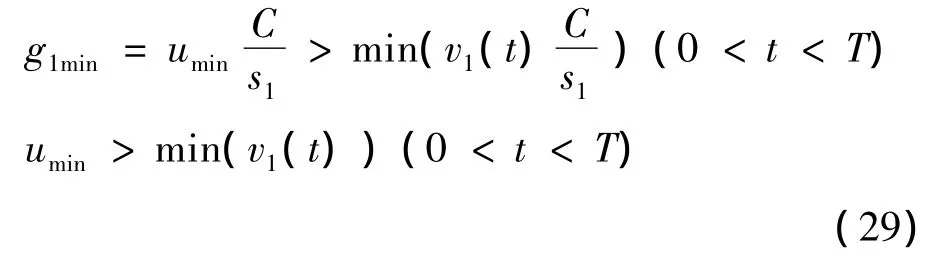
where T is the equalized queue duration time(T=T1=T2).Formula(28)and(29)indicate that the constraint of minimal effective green time has a significant impact on the performance of both groups，especially for the LP model because it is difficult to maintain the state of saturation flow in reality.

3.2 System optimal solution

If the constraint on the minimum green time is removed，the LP model provides a so-called system optimal solution in which the total intersection delay is further reduced.The solution of the same example is shown in Table 5.It is clear that the system optimal solution may not be practical since the drivers on approach 2 are punished too much.However，it provides an upper boundary threshold and can be used as a reference to evaluate other solutions.

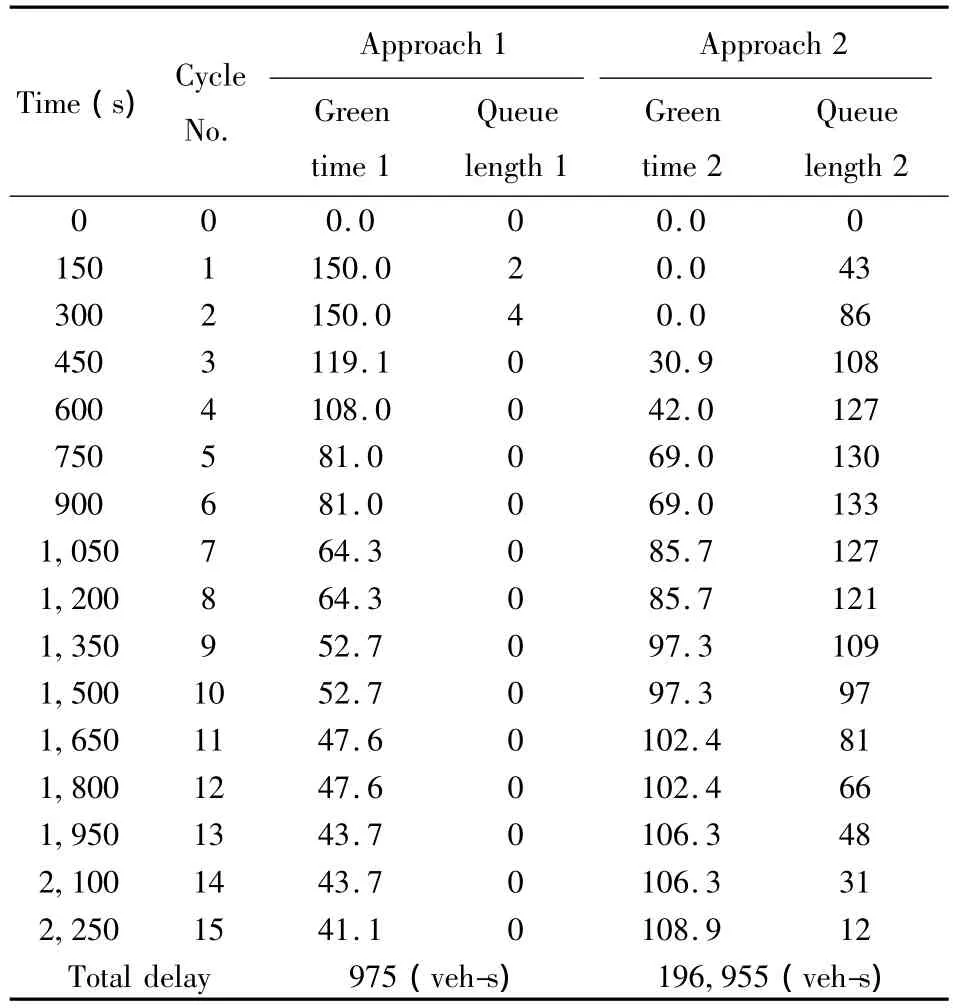
Table 5 Queue length and control strategy of system optimal solution

3.3 Evaluation of the queue dissipation patterns

The major difference between the two types of modelsis the queue dissipation pattern. Gazis proposed the principle that queues should be dissolved simultaneously for minimum intersection delay［2］.However，the assumption Gazis made is that:“throughput is the same in both directions so that the total throughput of the intersection remains constant.”The departure curves of two approaches D1and D2will thus be:

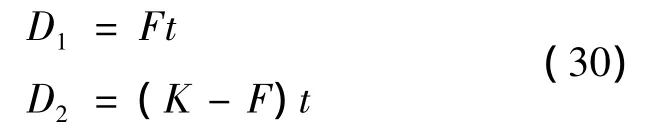
where K is a constant and F is the average service rate on approach 1，and:

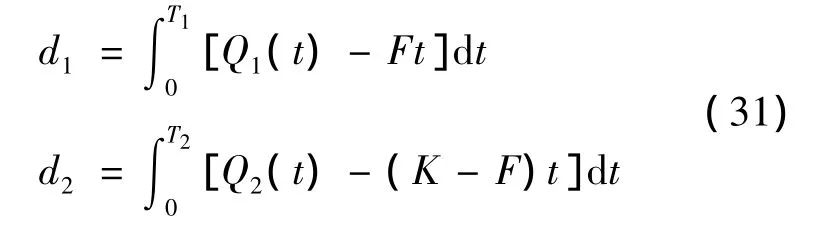
The total departure of each approach at the end of congested period is:

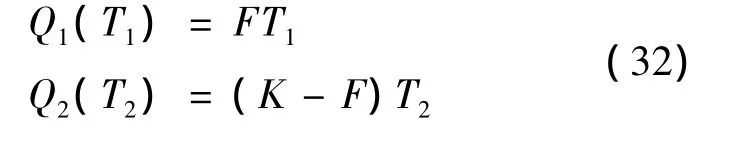
The total delay reaches minimum when:

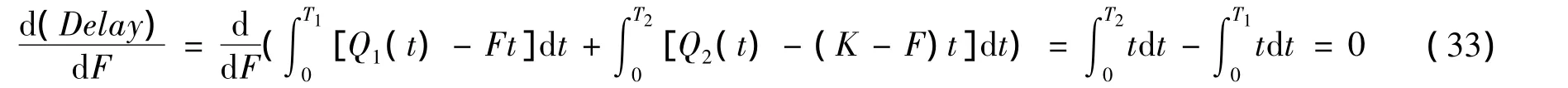
Therefore，T2=T1which indicates the queues will dissipate at the same time.

The fundamental assumption for the above result is that:“total throughput remains constant.”If the total throughput of one cycle is defined as P，then:

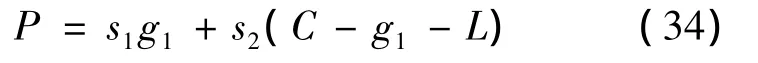
where L is the total lost time of the cycle and C is the cycle length.If the total throughput remains constant，then:

Equation(35)shows that the assumption Gazis made is valid only when S1=S2.In other words，dissolving queues simultaneously for delay minimization is valid only when the saturation flow rates of the(critical)approaches are equal or close.Therefore，the strategy should be only considered for the cases where the intersection approaches have same or similar saturation flow rates(e.g.，intersections at two major streets).If the saturate flow rates of intersection approaches are significantly different with each other(e.g.，where a major street intersects with a minor street)，the strategy of bang-bang type control cannot provide the optimal solution. This finding is of particularsignificance to traffic engineers when applying the Gazis’s principle to practice.

Applying the Gazis’s principle to other types of intersections cannot lead to an optimal solution.For the previous example，we keep the saturation flowrate of approach 2 constant(s2=1,000 pcu/h)and calculate the total delay by the bang-bang control strategy and compare the result with the system optimal solution with different saturation flow rates on approach 1(s1=1,000，1,200，1,400，1,600，1,800 pcu/h).By using the system optimal solution asa reference，the bang-bang controlstrategy becomes lesseffective with the increase ofthe difference in saturation flow rate.

The difference can also be visualized by inspecting Fig.3，which compares the bang-bang control with the system optimal solution by changing the saturation flow rates of the two intersection approaches. Forinstance， when S1/S2=1.8，compared to the system optimal solution，the bangbang control strategy increases total delay by about 21.6%.

4 Evaluation of synchro and TRANSYT-7F

Synchro and TRANSYT-7F are two widely used offline traffic signal optimization models.Both models have proven to be powerful tools when they are applied to undersaturated conditions. Recent development of the models also provides，to varying extent，strategies for timing oversaturated signals.Synchro and TRANSYT-7F are the models of choice because they represent the other two popular approachesin green time optimization. Synchro assigns green time among signal phases by using the Highway Capacity Manual’s method，which was basically designed for undersaturated signals;TRANSYT-7F’s green time allocation strategy is based on advanced formulation rather than a clearly defined phase switching policy.A comparison analysis of these two commercial tools and the classic models would be helpful for this study in assessing potential benefits of improved methods.As the focus of this paper is on isolated intersections，only their green time allocation/splits strategies are evaluated.

4.1 Synchro

Synchro is an offline signal optimization program which implements the Intersection Capacity Utilization(ICU 2003)and Highway Capacity Manual 2000(HCM 2000)for intersection capacity analysis and signal timing design.From Synchro 6，congested link analysis and optimization was included in the software package［21］. A new totaldelay conceptwhich includes the traditional control delay plus a new term of queue interaction blocking delay was embedded into Synchro 6.However，although the delay function was enhanced in terms of optimized cycle length and offset，there seems no improvement made on splits optimization.

In the latest version of Synchro 7，green time is allocated based on the flow ratio，which is the ratio of the flow rate and the saturation flow of the critical movement［21］. The split optimizer respects the minimum splitsetting foreach phase whenever possible.When optimizing splits，it first attempts to provide enough green time to serve the 90th percentile lane group flow.If there is no enough cycle time to meet this objective，Synchro attempts to serve the 70th percentile traffic and then the 50th percentile traffic.Extra green time，if any，is given to the main street.In under-saturated conditions，this method tends to give lower v/c ratios(Eq.(36))to the lane groups with low traffic demands.When traffic volume exceeds capacity，Synchro attempts to balance v/c ratios for each phase，while still respectingall minimums.

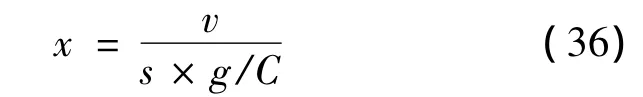
It is clear that in under-saturated conditions，Synchro’s policy for green time split is based on the adjusted Webster method which favors the main street phases.It is worthy of note that Synchro 5.0，6.0，and 7.0 uses the same strategy for oversaturated conditions.Furthermore，because of its singleperiod optimization method，Synchro cannotmodelthe accumulation of residual queues from one cycle to the next in oversaturated conditions.

4.2 TRANSYT-7F

TRANSYT-7F is another popular signal timing optimization tool，which applies genetic algorithm to optimize cycle length，phasing sequence，splits，and offsets.In its latest release，Version10.3［15］， a multi-period optimization process was added.The purpose of multi-period optimization is to develop an effective signal-timing plan for handling oversaturated conditions and residual queues.The program can optimize the splits and offsets of one timing plan across all time periods.Genetic algorithm(GA)optimization is a theoretical improvement over the traditional hill-climb optimization technique that has been employed by T7F formany years. Itis advantageous in searching the“global optimum”without being trapped in“local optimum”solutions.

4.3 Evaluation

The example used in section 4 is carried out to evaluate the performance ofSynchro 7.0 and TRANSYT-7F Version 10.3，the results are shown in Figs.4 and 5.Fig.4 illustrates the performance of Synchro，TRANSYT-7F，and the theoretical models in terms of the total intersection delay which is presented by the area between the arrivaland departure curves.

For oversaturated intersections，the length of queue needs to be carefully managed because the queues blocking back to the upstream intersection may cause serious damage to the whole system.Fig.5 compares the models’performance in terms of the queue length in number of vehicles.

It is not surprising that the system optimal model stands out from the others in both categories.But our earlier analysis has shown that this approach is not practical because of its extremely imbalanced green time allocation strategy.Here，it is used again as a reference.The bang-bang type of control performs fairly well，which is only next to the ideal solution from the system optimum model in both categories.The intersection delay from Synchro is slightly higher than that from the bang-bang strategy but the queue clearance time is almost the same.The LP model is next to the above three models due to its green time loss as described earlier.The TRANSYT-7F model，interestingly，performs least effectively in terms of intersection delay due to its relatively longer queue clearance time.

As for the queue length control，the three theoretical models outperform Synchro and TRANSYT-7F.As can be seen from Fig.5，the maximum number of vehicles in queue resulted from Synchro and TRANSYST-7F is over 150，which is higher than that from the three theoretical models.

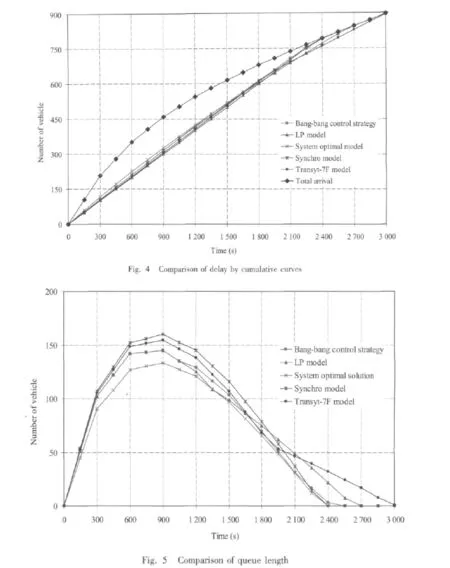
In summary，the findings from the evaluation can be summarized as follows:(1)The models with clearly defined phase switching or green time allocation policies(the bang-bang control models，the LP model，and Synchro)perform betterthan the formulation based approach TRANSYT-7F in both intersection delay and queue clearance time.(2)The classic models with policies specifically designed for the oversaturated conditions(the bang-bang control model and the LP model)are advantageous in queue management compared to Synchro，which uses the same policy for under-saturated signal design，and the formulation based TRANSYT-7F.(3)The bang-bang type control models developed on the basis of the simultaneous queue dissipation philosophy are applicable only to the situation that the saturation flow rates of(critical)intersection approaches are equal or close.In addition，traffic demands during the whole congested period must be given in advance，which makes the bang-bang control strategy difficult to implementin practice，especially for real-time applications.(4)The LP model can lead to the system optimal if the constraint on minimum green time is relaxed and the condition of saturation is satisfied at all intersection approaches during the entire congested period.The solution can be taken as a reference to scale the performance of the other models.

5 Conclusions

The authors examined two groups of classic models and compared their performance with TRANSYT-7F and Synchro in signal timing of isolated and pretimed intersections.Focuses were placed on their green time allocation or phase switching policies under oversaturated traffic conditions.The bang-bang type of models follow the policy that queues are discharged simultaneously on all (critical)intersection approaches;the LP model is consistent with the strategy thatpriority isgiven to the oversaturated approaches with higher saturation flow rates;Synchro follows the principle that green time is allocated based on the flow ratio of critical intersection approaches.These three models all allocate green time according to a clearly defined control policy.TRANSYT-7F，on the other hand，features signal timing optimization through advanced computation which does not rely on a predefined policy.

The analyses conducted in this research revealed the necessity of embedding the classical models(with clearly defined phase switching policy)with the existing signal timing tools.When these integrated toolsare applied， however， particularattention should be paid on the applicability of these models for best performance.For practical application of the results concluded from this research，the following guidance can be used for timing isolated oversaturated intersections.

(1)Intersections need to be classified based on their geometric layout(in terms of number of lanes at intersection approaches and associated saturation flow rates)and different type of intersections needs to be treated differently.

(2)For the intersections with asymmetric layouts(e.g.，the intersections crossed by a major and a minor road)，the policy of giving priority to the major street with higher saturation flow rate should apply and the LP model can be used.Particular attention should be paid to two points for best performance:(a)the minimum green interval of minor streets needs to be carefully designed to avoid effective green time loss;(b)the growth of residual queue needs to be restrained according to the storage capacity of the link to avoid queue spilling back to the upstream intersection.

(3)For the intersections with symmetric layout and without significant difference in saturation flow among(major)intersection approaches(e.g.，the intersections crossed by similar class of roads，minor＆ minorormajor＆ major)，the policy of simultaneous queue discharging and bang-bang type of models can be applied if the traffic demands during the entire congested period is available in advance.Otherwise，the policy ofassigning green time according to flow ratio(i.e.，Webster’s method)would be sufficient and Synchro type of tools will work.

［1］Gazis D C，Potts R B.The Oversaturated intersection.Proc.，2nd Int.Symp.on Theory of Road Traffic Flow，Paris，France，1963，221-237.

［2］Gazis D C.Optimal control of a system of oversaturated intersections.Operations Research，1964，12:815-831.

［3］Michalopoulos P G，Stephnopolos G.Oversaturated signal systems with queue length constraints-I single intersection. Transportation Research 11， 1977，413-421.

［4］Chang T H，Lin J T.Optimal Signal timing for an oversaturated intersection.Transportation Research，Part B，2000，34(6):471-491.

［5］Chang T H，Lin J T.Optimal Signal timing for an oversaturated intersection.Transportation Research，Part B，2004，38(8):687-707.

［6］Yin Y.Robust optimal traffic signal timing.Transportation Research Part B，2008，42:911-924.

［7］Dans G，Gazis D C.Optimal control of oversaturated store-and forward transportation networks，Transportation Science，1976，11(1):1-19.

［8］Lieberman E B，Chang J，Prassas E S.Formulation of real-time control policy for oversaturated arterials.Transportation Research Record 1727，Transportation Research Board，Washington，D.C.，2000，77-98.

［9］Lo H K，Chow A H.Control strategies for oversaturated traffic.J.of Transp.Eng.，2004，130(4):466-478.

［10］Won C K，Wong S C，Lo H K.A special queuing approach to optimize coordinated signal settings to obviate gridlock in adjacent work zones.Journal of Advanced Transportation，2010，44:231-244.

［11］Park B，Messer C J，Urbanik II T.Traffic signal optimization program foroversaturated conditions:genetic algorithm approach.Transportation Research Record 1683， Transportation Research Board，Washington，D.C.，1999，133-142.

［12］Park B，Messer C J，Urbanik II T.Enhanced genetic algorithm for signal-timing optimization of oversaturated intersections.Transportation Research Record 1727，Transportation Research Board，Washington，D.C.，2000，32-41.

［13］Abu-Lebdeh G，Benekohal R F.Genetic algorithm for traffic signalcontroland queue managementof oversaturated two-way arterials. Transportation Research Record 1727，Transportation Research Board，Washington，D.C.，2000，61-67.

［14］Li H，Prevedouros P D.Traffic Adaptive control for oversaturated isolated intersections: Model development and Simulation testing.J.of Transp.Eng.，2004，130(5):594-601.

［15］Hale D.Traffic Network Study Tool-TRANSYT-7F.McTrans， University of Florida， Gainesville，Florida，2006.

［16］Transportation Research Board(TRB).Highway Capacity Manual 2000［M］，Transportation Research Board，Washington，D.C，2001.

［17］Daganzo C F.Fundamentals of Transportation and Traffic Operations.Pergamon，New York，1997.

［18］Webster F V.Traffic signal settings.Road Research Technical Paper，No.39，Road Research Laboratory，London，1958.

［19］Fang F C，Elefteriadou L.Modeling and simulation of vehicle projection arrival-discharge process in adaptive traffic signal controls. Journal of Advanced Transportation，44(1010)176-192.

［20］Michalopoulos P G，Stephnopolos G.Optimal control of oversaturated intersections theoretical and practical considerations.Transportation Engineering ＆ Control，1978，5:216-221.

［21］Husch D，Albeck J.Trafficware SYNCHRO 7 User Guide，Trafficware，Albany，California，2004.