“几何画板”绘制机械振动的关系图示
2013-09-19王明美
王明美
(合肥师范学院,安徽 合肥 230601)
按振动系统的受力或能量转换情况,振动可分为自由振动和受迫振动。自由振动又可分为无阻尼自由振动和阻尼振动。最基本的振动是谐振动。任何复杂的振动都可看作有若干个谐振动的叠加[1-4]。几何画板绘制图示有多种方法,常用的参量函数轨迹法包括三个重要步骤,即在合适的坐标系上设置参量、设置函数、构造轨迹,应用实例可详见文献[2-3],以下将此法用于绘制机械振动的各种关系图示。
1 谐振动中的位移与时间关系的图示
谐振动中的位移与时间的关系为

以下是《几何画板5.05》的操作步骤。
(1)新建画板文件。使用菜单命令“文件/另存为”,将画板文件保存为“机械振动模拟.gsp”。
(2)设置直角坐标系。选择“自定义工具/蚂蚁坐标系/直角坐标系[无参数]”,单击选择[系统初始化],出现x0y坐标系,设置为第一象限,隐藏刻度线,隐藏刻度值。
(3)设置自变量。用“点工具”在x轴上作点P,选中A,执行菜单命令“度量/横坐标”,出现自变量x的取值,此例中的自变量为角频率w。
(4)设置参量。振幅A、角频率w、初相位a。用线段工具作线段A,选中线段,执行菜单命令“度量/长度”出现线段A的长度取值,将线段的标签改为A,并测出长度。使用“数据/新建参量”,分别新建另两个参数,角频率w=1,初相位a=60可以不用单位。
(5)设置函数y。执行菜单命令“数据/计算”,在“新建计算”对话框中输入函数
(6)作出函数的点。选中自变量x的取值和应变量y函数,使用菜单命令“绘图/绘制点(x,y)”得P点。
(7)作图。选中A点和P 点,使用菜单命令“构造/轨迹”,现在可以将横坐标的标签改为t,纵坐标的标签改为x,隐藏不需要显示的点和线,完成图1中的谐振动位移与时间的关系。

图1 谐振动位移与时间的关系图示
2 阻尼振动的位移与时间关系的图示
阻尼振动的位移与时间的关系为

使用参量函数轨迹法。取φ0=0,设置参数为A0=5、δ=1和w=5,函数有三个,图中的实线对应的函数是, 虚线对应的函数是作图1的步骤,分别作出三条函数图线,最后将横坐标和纵坐标的标签分别改为t和x,见图2。
3 不同阻尼下的阻尼振动和阻尼过大时的非周期运动的图示
用实线、虚线和点状线分别表示欠阻尼(δ<ω0)振动、过阻尼δ>ω0和临界阻尼δ=ω0时的位移与时间的关系图示。
使用参量函数轨迹法。取φ0=0,设置参数为A0=6、δ=1和ω0=6,函数有三个,欠阻尼振动的函数是过阻尼的函数是临界阻尼的函数是按照制作图1的步骤,分别作出三条函数图线,最后将横坐标和纵坐标的标签分别改为t和x,见图3。
4 受迫振动的位移与时间曲线
受迫振动的位移与时间的关系为


图3 不同阻尼下的阻尼振动和阻尼过大时的非周期运动
使用参量函数轨迹法。取φ0=0,φ=0设置参数为A0=3.20、A=3.30、δ=0.2、w0=10和Acos(50ωdx)。按照制作图1的步骤,作出函数图线,最后将横坐标和纵坐标的标签分别改为t和x,见图4。

图4 受迫振动的位移与时间的关系图示
5 受迫振动的速度振幅值与外力频率的关系图线
受迫振动的速度振幅与外力频率的关系为

式中γm为速度振幅值,F0为驱动外力的幅值,m为振子的质量,ω0为振子的固有角频率,φd为驱动外力的角频率,δ为阻尼系数。
使用参量函数轨迹法分别作出阻尼较大、阻尼较小的三条实线。设置参数为F0/m=8、ωd,函按照作图1的步骤,分别作出三条函数图线,最后将横坐标和纵坐标的标签分别改为γm和ωd,见图2。
为了绘制时的两条虚线,需要用到分段函数法,设此时的函数分别为
当ω<ωd时
当ω>ωd时
最后,在ω=ωd处设置一条虚线,见图5。
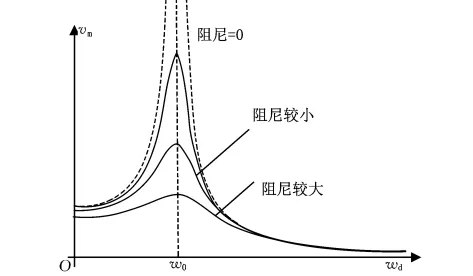
图5 受迫振动的速度振幅值与外力频率的关系
用几何画板绘图,不仅操作简单,形象直观,而且利用修改参数形成动态图示演变效果,有利于教学。参数函数轨迹法作为常用绘图法具有操作步骤少、易于操作、而效果明显的特点[5-6]。
[1]程守洙,江之永.普通物理学(下册)[M].6版.北京:高等教育出版社,2006:1,4,21,23,24.
[2]安宝生.中小学教师信息技术培训[M].北京:北京师范大学音像出版社,2001:241-251.
[3]刘胜利.几何画板与微型课件制作[M].北京:科学出版社,2001.
[4]喻力华,陈昌胜.用matlab软件模拟振动实验[J].大学物理实验,2011,24(3):79-81.
[5]刘成华.运用几何画板探究动态物理问题的策略研究[J].物理通报,2007(10):43-45.
[6]戴湘云,韩建光.几何画板中的交互功能[J].山东教育,2003:54-55.
