一种基于距离图的QC-LDPC构造算法

杨 帆，文晓聪，张会生，李立欣，王鲁杰

（西北工业大学 陕西 西安 710129）

自从LDPC码被发现以来，许多专家学者都致力于寻找好的构造算法，要求构造的LDPC码既要具有优异的译码性能，又有较低的硬件实现复杂度。目前LDPC的构造方法主要有两类，一类是随机构造法，另一类是结构构造法。与结构码相比，随机码具有更好的译码性能，特别是在码长较长的情况下[1]。 例如，BF[2]、PEG[3-4]等随机构造法得到的 LDPC码能够使圈长达到最大，同时其码长、码率、圈长等参数选择比较灵活，但由于行列之间的连接不确定性，大大增加了硬件实现复杂度。结构构造法对校验矩阵的行列之间的连接进行一定地约束，使之具有结构性，减小了硬件编译码复杂度，但是一般的结构码在码率、码长和圈长等方面的限制，减少了其应用范围。

本文利用了随机构造的思想，并加入了一些约束行条件，提出了一种基于距离图的搜索算法，它有两种实现方式—顺序搜索方式和随机搜索方式。这种算法能够保证得到的LDPC码具有准循环特性和给定的圈长，并且码率、码长和圈长等参数能够在很大范围内选取。仿真结果表明：随机搜索方式的性能明显优于顺序搜索方式；文中采用随机搜索方式构造的（1 500，3，6）QC-LDPC码，具有非常优异的误码率性能，与随机码接近，当信噪比为3时，误码率甚至可以达到10-9。与随机构造法相比，这种算法构造的码都具有准循环特性，因此易于硬件编码和译码，并且构造速度更快；与其他结构构造法相比，该算法更加灵活，应用范围也大大增加。

1 距离图的定义

距离图中的一个循环是由顶点x为起点并以x为终点的一条闭合路径构成的，最短的循环称为最小圈长，简称圈长（girth）。在距离图中，长度为g的循环相当于校验矩阵中长度2g为的循环。距离图中圈长等于闭合路径中顶点个数或边数，而在校验矩阵中，圈长等于“1”的个数，所以距离图中的圈长为校验矩阵圈长的一半。图1（a）中的虚线代表一个长度为3的循环，对应的校验矩阵循环长度为6，如图1（b）中虚线所示。

距离图和校验矩阵是一一对应的关系，可以利用不同的距离图得到不同的校验矩阵，从而构造出许多种不同长度、码率、girth大小的准循环LDPC码。接下来将介绍基于距离图的LDPC码的搜索算法。

图1 LDPC码的距离图以及对应的校验矩阵Fig.1 Structure diagram of the distance graph and the corresponding check matrix

2 基于距离图的搜索算法

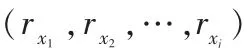
1）假设一个LDPC码的距离图的顶点个数为M，行重为k，列重为j，顶点的个数即为校验矩阵的行数。将行（或者顶点）分成 j个大小相等的组，记为（G1，G2，…，Gj）。 每个组包含p行，其中p=M/j，p一定要大于理论上的最小值。第x行记为rx，Uxj记为所有与rx距离不超过g的行的集合。在距离图上，两个行（或顶点）最短路径的边数作为两个行（或顶点）之间的距离，g就是期望的圈长的一半。

2） 将（G1，G2…，Gj）一共 j个组作为一个子组，一共取 k个这样的子组，子组依次标记为（GP1，GP2…GPk）。

3） 对于每个子组 GPt，令 t=1，2，…，k：

①从GPt中选取第一组G1作为参考组；

②从G1中选取第一行r1作为参考行；

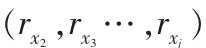
④令:z=1，…，p-1

如果（rx2+z，rx3+z…，rxj+z）与 r1+z的距离至少为 g，则使 r1+z与（rx2+z，rx3+z…，rxj+z）相连，连接完成之后，则转入第 3）步继续执行，直到循环结束。否则重新执行上一步操作3。

4）把得到的距离图转换为LDPC的校验矩阵H。距离图中的顶点对应H矩阵的行，j个顶点的每一次连接都构成H矩阵的一列。

5）将得到的H矩阵按列分成k块，每一块的大小为p，对每一块进行循环移位操作，移位偏量q随机选择，q∈{0，1，…，p-1}。

这两种算法构造的LDPC码的结构、误码率性能上会有较大的差异。下面分别介绍这2种搜索方式。

2.1 顺序搜索方式

图2是利用顺序搜索方式构造一个圈长为8的（20，2，4）QC-LDPC的过程。由图可知，行的总个数M等于10，行组的个数为2，因此每组的大小p为5，记为组1和组2，组 1 为（r1，r2，r3，r4，r5）行，组 2 为（r6，r7，r8，r9，r10）行。 由于行重k=4、列重j=2，因此子组的个数为4，每个子组都由组1和组2组成。每个子组需进行一次连接操作，因此一共进行4次连接过程。要求构造的LDPC码的圈长为8，因此距离图中两行之间的距离不能小于4。第一次连接，顺序搜索组2中第一行即r6，由图可知满足与参考行r1的距离大于等于4的条件，因此使 r6和行 r1相连，组 1 剩下的行（r2，r3，r4，r5）分别与组 2 剩余的行（r7，r8，r9，r10）相连。第二次连接，顺序寻找到组 2的下一行即r7，由图可知r7满足与参考行r1的距离不小于4的要求，因此使 r7与 r1相连，使剩余的行（r2，r3，r4，r5）分别与（r8，r9，r10，r6）相连。 第三次连接，顺序寻找到组 2 中的下一行r8，由图可知r8满足与参考行r1的距离不小于4的要求，因此使 r8与 r1相连，同理使行（r2，r3，r4，r5）分别与行（r9，r10，r6，r7）相连。第四次连接，顺序寻找到组2中的下一行r9，由图可知r9满足与参考行r1的距离不小于4的要求，因此使r9与r1相连，同理使行（r2，r3，r4，r5）分别与行（r10，r6，r7，r8）相连，这样就完成了四次连接过程，并且图中不存在长度为4的循环，满足了圈长为8的要求。图3为顺序搜索时对应的校验矩阵。由图可知，校验矩阵按列分为4个块，每一块对应一次连接过程；按行分为两部分，上部分对应（r1，r2，r3，r4，r5）行，由 4 个 5×5 的单位子矩阵组成的，下部分对应（r6，r7，r8，r9，r10）行，由 4 个循环移位子矩阵组成。由于采用顺序搜索方式，因此分别向左循环移0、1、2、3位。图4是对图3中的校验矩阵进行随机循环移位（即随机列变换）所得到的校验矩阵，每一块分别向右循环移 3、1、2、2位，增加了“1”分布的随机性。 由图 4可以看出不存在长度小于8的循环。

图2 顺序搜索时圈长为8的（20，2，4）码的距离图构造过程Fig.2 Graph representation of the construction process of a girth-8（20，2，4）code using sequential search

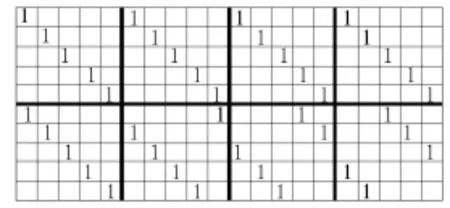
图3 顺序搜索时圈长为8的（20，2，4）码对应的校验矩阵Fig.3 Check matrix representation of a （20，2，4）code with girth eight using sequential search

图4 随机循环移位得到的校验矩阵Fig.4 Obtained check matrix using random cyclic shift

2.2 随机搜索方式

图5是采用随机搜索方式构造一个圈长为8的（20，2，4）QC-LDPC的过程。第一次连接，随机选择组2中的行r8，由图可知r8与参考r1的距离大于4，因此使r8与r1相连，并且分别使组 1 剩下的行（r2，r3，r4，r5）分别与组 2 剩余的（r9，r10，r6，r7）相连。 第二次连接，随机搜索到行 r6，由图可知 r6与r1的距离大于4，使行r6与r1相连，并且使组1中剩下的行（r2，r3，r4，r5）分别与组 2 剩余的行（r7，r8，r9，r10）相连。 第三次连接随机搜索到行r10，由图可知与r1的距离大于4，同理使行（r1，r2，r3，r4，r5）分别与行（r10，r6，r7，r8，r9）相连。 第四次连接，随机搜索到r7，由图可知r7与参考行r1的距离不小于4，因此使行（r1，r2，r3，r4，r5）分别与行（r7，r8，r9，r10，r6）相连。 经过 4 次这样的连接，就构成了一个完整的距离图。

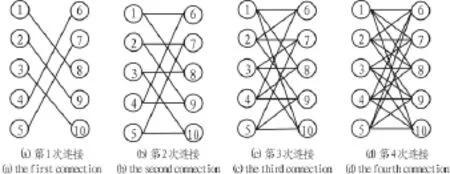
图5 随机搜索时圈长为8的（20，2，4）码的距离图构造过程Fig.5 Graph representation of the construction process of a girth-8（20，2，4）code using random search

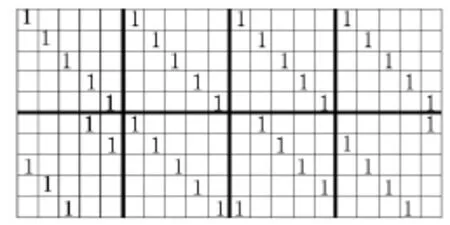
图6 随机搜索时圈长为8的（20，2，4）码对应的校验矩阵Fig.6 Check matrix representation of a （20，2，4）code with girth eight using random search

图7 随机循环移位得到的校验矩阵Fig.7 Obtained check matrix using random cyclic shift

图6是采用随机搜索方式时对应的校验矩阵。图6的上半部分是由4个的单位字矩阵构成，下半部分是由四个循环移位字矩阵构成，分别向右循环移3位、0位、1位、4位。由于采用随机搜索的方式，因此4个循环移位子矩阵的移位偏移量也是随机的。由图可以看出非零元“1”的分布比顺序搜索方式更加具有随机性，因此误码率性能也将会提高。图7是对图6中H矩阵进行随机循环移位所得的校验矩阵，每一块的分别向右循环移 3、3、1、0 位，这样非零元“1”的分布更具有随机性。

3 算法的复杂度分析

假设LDPC码的行数为M，行重为k，列重为j，那么算法的复杂度分析如下。

1）行组的个数为j，每一行组的的大小为p=M/j；

2）对于每一个子组，非参考组里的每一行，在算法搜索之前需要更新与参考行r1的距离，如果要求与参考行的距离不小于g，那么每次更新需要g步运算。对于一个行组，则要进行pg次运算，因为一共有j-1个非参考行组，因此一共需要pg（j-1）次运算，才能完成更新运算。

由此可知，算法的实现复杂度与码长成正比，因此一般情况下能够较快的构造出所需的码字。算法的复杂度还与实现的搜索方式有关，顺序搜索法可能会需要很长的时间，特别是当行组p很大时。对于行组p越大的码，搜索算法成功的机率越大期望的圈长可以设置的越大。利用上文中基于距离图的搜索算法可以很容易得到圈长为6、8、10甚至超过12的码。

4 仿真结果

本文利用基于距离图的两种构造方式—随机搜索方式和顺序搜索方式，构造了一组圈长为分别为6、8、10的QCLDPC码，其码长为1 500，行重和列重分别为6和3。为了进行对比，用 PEG 算法构造一种圈长为 8的（1 500，3，6）PEG随机码。仿真是在AWGN信道下，采用BPSK调制，译码采用了基于整数运算的最小和译码算法[7]，迭代次数20次。图8是采用随机搜索方式下（1 500，3，6）码的性能仿真图。图9是采用顺序搜索方式下（1 500，3，6）码的性能仿真图。图10是2种搜索方式的性能比较图。从以上3个仿真图可以得出：随机搜索方式的性能明显优于顺序搜索方式；采用同样方式构造的码，随着圈长的增大误码率性能越来越好；在相同的圈长下，PEG算法比文中随机搜索方式的性能好，但相差不大；本算法中随机搜索方式构造的QC-LDPC码性能非常优异，当SNR为3 dB时，误码率甚至可以达到10-9，非常适合小信噪比环境下通信。

图8 采用随机搜索方式时得到码的误码率性能Fig.8 BER performance curves for codes using random search

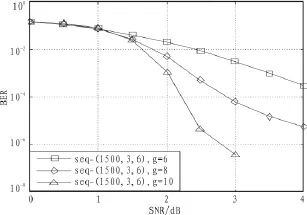
图9 采用顺序搜索方式时得到码的误码率性能Fig.9 BER performance curves for codes using sequential search

图10 两种搜索方式的误码率性能比较Fig.10 BER performance curves for codes using sequential search and random search

5 结 论

文中设计了一种基于距离图的搜索算法，它有两种实现方式—顺序搜索方式和随机搜索方式，其中随机搜索方式的性能更优，与随机码的性能接近。这种构造算法具有以下几个优点：第一，圈长可以设定，能够构造出圈长为6、8、10甚至12的QC-LDPC码；其次，其行重、列重和码长在一定条件下也可以设定，灵活性好，适用范围大；此外，与随机构造法相比，这种搜索算法构造的LDPC码具有准循环特性，易于硬件实现，并且构造速度更快；第四，文中采用随机搜索方式构造的 （1 500，3，6）QC-LDPC码，具有非常优异的误码率性能，与随机码接近，当信噪比为3时，误码率甚至可以达到10-9，非常适合小信噪比环境下通信。

[1]HU Xiao-Yu.Progressive edge-growth tanner graphs[D].Switzerland:the SwissFederalInstitute ofTechnology Lausanne，2001.

[2]Campello J，Dodha D S，Rajagopalan S.Designing LDPC codes using Bit-Filling [C]//In Proceedings of the International Conference on Communications，2001:55-59.

[3]Uchoa A G D，Healy C， de Lamare，et al.Design of LDPC codes based on progressive edge growth techniques for block fading channels[J].IEEE Communication Letters，2011（15）:1221-1223.

[4]HUANG Li-qun，WANG Yu-liang，GONG Ping.An improved construction method of QC-LDPC codes based on the PEG algorithm [C]//Circuits， Communications and System（PACCS），2011:1-4.

[5]Fossorier M P C.Quasi-cyclic low-density parity-check codes from circulant permutation matrices[J].IEEE Transactions on Information Theory，2004，50（8）:1788-1793.

[6]Sullivan M E O.Algebraic construction of sparse matrices with large girth[J].IEEE Transactions on Information Theory，February 2006，52（2）:719-727.

[7]LI Li-xin，CHEN Zheng-kang，FAN Jie，et al.Implementation of LDPC codes decoding based on maximum average mutual information quantization[J].International Review on Computers and Software （I.RE.CO.S.），2011:1135-1139.