二次曲线（面）所围图形的面（体）积

汤 宇1，赵 虹2

(1.吉林工商学院基础部，吉林长春 130062；2.长春师范学院数学学院，吉林长春 130032）

二次曲线（面）所围图形的面（体）积

汤 宇1，赵 虹2

(1.吉林工商学院基础部，吉林长春 130062；2.长春师范学院数学学院，吉林长春 130032）

本文首先讨论二元(三元)二次曲线(面)所围封闭图形的面(体)积计算，之后将结果推广到n元二次曲面所围n维封闭图形的体积，并给出所围n维封闭图形体积的一般表达式.

二次曲(线)面；n维超椭球体；体积；欧拉函数

由解析几何[1]知二次曲线表示的图形有9种，非退化的实轨迹有3种：椭圆、双曲线、抛物线，只有椭圆为封闭图形；二次曲面有17种，非退化有实轨迹的有5种：椭球面、单叶双曲面、双叶双曲面、椭圆抛物面、双曲抛物面，其中只有椭球面为封闭图形.本文将讨论这些封闭图形所围图形的面积或体积，并给出在二次曲线或二次曲面为一般表达式下的所围图形的面积或体积公式，最后将结果推广到一般n元超曲面所围超立体体积.

1 基本知识

定义1x,y关于的二元二次的实系数方程

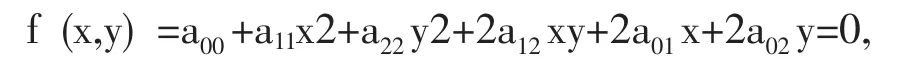
（其中a11,a12,a22不全为0）所表示的曲线，称为地次曲线，分别称

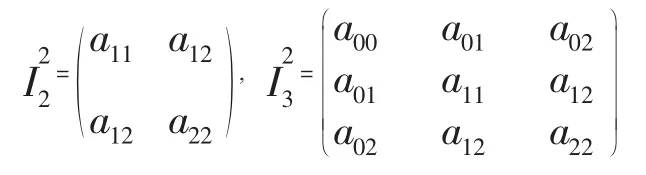
为二次曲线的二次项系数矩阵和系数矩阵.

称det(-λE)=0为二次曲线的特征方程，其根称为二次曲线的特征根.

定义2 称关于x,y,z的三元二次实系数方程

（其中a11,a22,a33,a12,a13,a23不全为0）表示的曲面称为二次曲面，分别称为二次曲面的二次项系数矩阵和系数矩阵.

称det-λE)=0为二次曲面的特征方程，其根称为二次曲面的特征根，同样利用矩阵乘法，可把f(x,y,z)表示为，称为二次曲面的矩阵表示.

定理1.1的证明见一般的空间解析几何书[1].

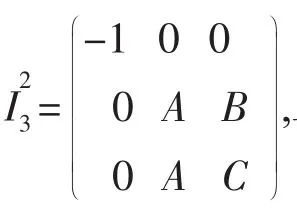
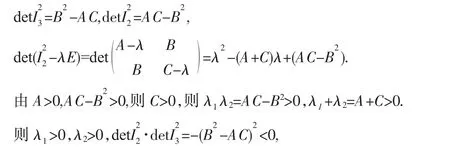
由定理1.1的(2)知f(x,y)=Ax2+2Bxy+Cy2-1=0 在A＞0，AC-B2＞0 时表示椭圆.

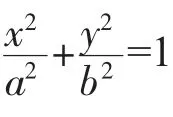
证明见一般的数学分析书[2].

2 二次曲线所围图形的面积

定理2.1 二次曲线f(x,y)=(1x y)(1x y)T=0在表示椭圆时，其面积为

又由特征根性质，λ1λ2=det,则

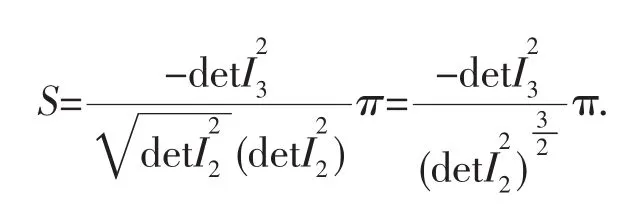
I=时，表示的椭圆所围的面积为

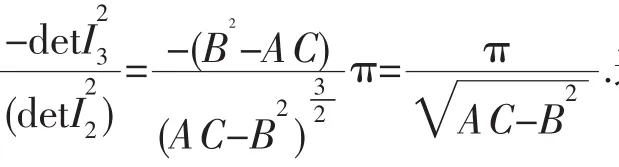
3 二次曲面所围图形的面积

定理3.1 二次曲面一般方程f(x,y,z)=(1x y z)I(1x y z)T=0时在表示椭球面时，其所围成的体积为

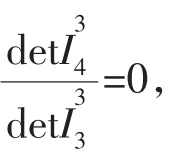
注 一元的二次函数f(x)=a00+a11x2+2a01x=0也有类似结论.

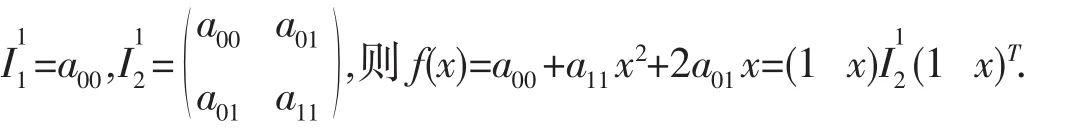
在a11＞0,a012-a00a11＞0时，能围一线段（即两个实根间线段），且此线段长为

4 n元二次超曲面围超椭球体体积

由上面的推导此可推测，对n元二次超曲面

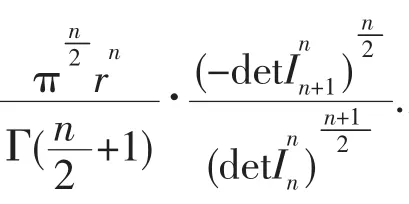
[参 考 文 献]

[1]周建伟.解析几何[M].北京:高等教育出版社,2005.

[2]华东师范大学数学系.数学分析下册[M].4版,北京:高等教育出版社,2010.

[3]林源渠,方企勤.数学解题指南[M].北京:北京大学出版社,2003.

Areas(Volumes)of N-dimension Ellipsoid Enclosed by Quadratic Curve(Surface)

TANG Yu1,ZHAO Hong2
(1.Department of Basic Course,Jilin Business and Technology College,Changchun Jilin 130062,China；2.Department of Mathematics,Changchun Normal University,Changchun Jilin 130032,China)

This paper deals with area（volume）calculation of enclosed graphic by quadratic curve(surface).The result has been generalized to the case of the volume calculation of enclosed graphic by n-variete quadratic surface.At last,general expression of volume of n-dimension enclosed graphic are given.

quadratic curve(surface)；n-dimension ellipsoid；volume；Euler Function

O174

A

1008-178X(2013)01-0004-04

2012-10-16

长春师范学院自然科学基金资助（长师院自科合字政策[2010]第019号）。

汤 宇（1971-），女，吉林长春人，吉林工商学院基础部副教授，硕士，从事函数论研究。