谈文科生数列极限概念的教学设计

张文军

（长春师范学院初等教育学院，吉林长春 130032）

谈文科生数列极限概念的教学设计

张文军

（长春师范学院初等教育学院，吉林长春 130032）

本文借助实例及几何图形的描述，从静态到动态、有限到无限、具体到抽象的认识过程来探讨数列极限概念的教学设计过程。

高等数学；文科生；数列极限；教学设计

对于大一新生来说，他们一方面对高等数学充满了新鲜感和神秘感，另一方面他们的学习方法和思维方式往往还停留在初等数学学习阶段，很少涉及“无限”概念，习惯于用一种静态不变的观点来分析问题，而这正是学习高等数学需要转变的。对于文科学生来说，这点更为明显。因此对文科生高等数学概念的教学应该是重在理解，讲求应用。《数列极限的概念》这节课的显性内容不多也不复杂，但它隐含的意义却是经典的、深邃的，由它衍生了“连续”“导数”“微积分”等诸多重要概念，对其理解实质上就是一种数学思想的渗透、一种数学思维方式的建立，它对后续内容的学习起着举足轻重的作用。总结以往的教学经验，为了使学生尽快地找到学习这门课程的基本方法，笔者从五个方面来阐述对这节课的设计。

1 模型驱动，认识“无限”

首先设计了以下两个问题：

问题1“我们都知道，一条线段是由无数个点组成的。请大家思考：这些点的长度是多少？”（出示课件）

对于这个问题，学生从没想过“这些点”有长度，他们的好奇心一下子被激发起来。学生踊跃发言，热烈讨论，可是却找不到正确答案。因为这个问题在初等数学的有限范围内是解决不了，那么引入“无限”概念就势在必行。

问题2《庄子·天下篇》中有这样一句话：“一尺之棰，日取其半，万世不竭”（出示课件）。并用数轴表示出来。

(1)每次截取完后，剩余长度是多少？(2)这个过程会不会完结？

学生易于解答这两个小问题，并得到如下数列（继续演示课件）

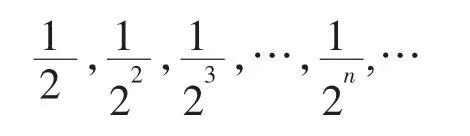
通过问题1和问题2这种“剥洋葱”式的问题串，引发学生强烈思想冲突和数学思考，同时也向学生释放出一个信号：从现在开始，我们要研究无限数列，教师可以就势给出无穷数列的定义。

定义1无穷数列的定义 按一定次序排列的无穷多个数x1,x2,…,xn,…成为无穷数列，简称数列，可简记为{xn}。其中的每个数称为数列的项，xn称为通项（一般项），n称为{xn}的下标。

接下来通过观察5个数列的变化趋势来进一步深化思维，直观极限的概念（演示课件）。

2 深化思维，直观概念

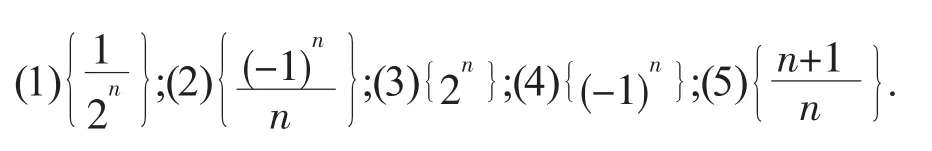
学生通过对这些数列的比较、观察，可以得出它们各自的变化趋势适时指出：像(1)、(2)、(5)这样的无穷数列称为有极限的数列，而这个常数称为该数列的极限。接下来和学生一起得到数列极限的描述性概念（出示课件）。这个概念虽然比较笼统，却为下一步精确定义奠定了基础。

针对这个定义，利用计算机模拟刘徽割圆术，介绍我国古代数学家对数列极限思想所做的贡献，其一是通过史料的简单介绍对学生进行爱国主义教育；其二是在概念形成阶段，为学生提供感性认识的基础；其三可对学生所得的结论加以验证、完善，加深对问题的理解，巩固所学的概念。通过这一实例，学生加深了对“无限增大”、“无限趋近于”、“极限”等概念的直观认识，初步感知从有限中认识无限，从量变中认识质变的这种极限思想，既突破了难点，又对学生进行了爱国主义教育。

概念中的“无限增大”与“无限接近”很模糊，增大到什么程度？接近到什么程度？用数学语言如何表述？需要进一步对学生进行讲解。

3 突出重点，精确概念

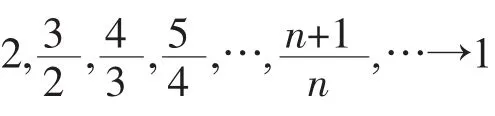
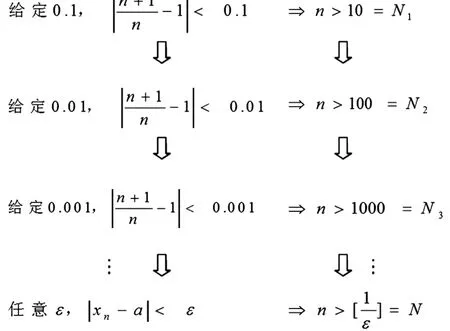
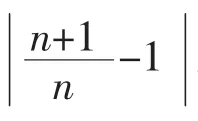
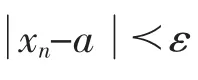
在这个过程中，学生通过由特殊到一般再到特殊的认识规律，“经历了概念的形成过程”[3]。这样，数列极限的精确概念在层层递进的教学活动中揭开了神秘的面纱，完全展现出来了。

4 巩固成果，定性分析

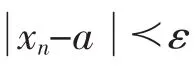
5 数形结合，感性回归

回归到概念的几何意义，学生会进一步明确数列极限的概念。极限的概念不是一节课就能完全建立起来的，它需要一个逐渐的过程。正如北宋思想家张载说：“教之而不受，虽强告之无益。”因此，作为极限概念这部分的教学是以问题解决为主线，充分发挥学生主体作用，引发学生的数学思考，主动探索，亲身体验数学概念形成的过程，对文科生理解数列极限概念起到很好的学习效果。

[参 考 文 献]

[1]刘仁云,赵虹.高等数学[M].北京:科学出版社,2011:19-22.

[2]同济大学应用数学系.高等数学[M].5版,北京:高等教育出版社,2002.

[3]顾庆凤.数列极限定义的教学过程设计探讨[J].科技创新导报,2011(34):152.

On the Teaching Design of Limit of a Sequence Concept for the Students Studying Liberal Art

ZHANG Wen-jun

(Changchun Normal University，Changchun Jilin 130032，China)

The paper explores the teachingdesign ofthe concept oflimit ofa sequence in the cognitive process of from static to dynamic states,from finite to infinite,from concrete to abstract by means of the description of cases and geometrical figures.

higher mathematics;the students studyingliberal arts;the limit ofa sequence;teachingdesign

G642

A

1008-178X(2013)01-0119-03

2012-10-05

张文军（1975-），男，吉林长春人，长春师范学院初等教育学院讲师，硕士，从事小学数学教育教学研究。