应用弹簧－质点模型的图像边缘检测算法的改进

高 山，邱明国，张绍祥，廖大成

(中国人民解放军第三军医大学 a.学员旅十三队;b.医学信息与医学图像学教研室;c.基础部解剖学教研室，重庆 400038)

数字图像的边缘是指灰度值发生剧变的区域分界线。边缘处包含大量的图像信息，因此如何使边缘尽可能真实、精细地凸显出来，对图像的后续处理(如特征提取、模式识别等)具有重要意义。目前用于图像边缘检测的算法很多［1－8］，经典的有 Roberts、Prewitt、Sobel、LOG 和 Canny 等。它们在边缘定位、抗噪声能力、方向性、检测的精细程度和真实程度等方面各有优劣［1］。

目前基于物理模型的边缘检测方法的文献报道尚不多。Sun等［9］根据万有引力定律建立力学模型，将图像的像素点看作宇宙中的天体，将灰度值看作天体的质量，根据万有引力公式及力的矢量叠加计算出某一个像素点受到周围点万有引力的合力，若该合力大于给定的阈值则判定该像素点为组成边缘线的点。Lopez-Molina等［10］对该方法进行了改进。

弹簧－质点模型最初用来进行布料等织物运动变形的计算机仿真［11－13］。徐遥等［14］受力学模型的启发提出了基于弹簧－质点模型的图像边缘检测算法:将像素点视为质点，相邻像素点间用相同材质、不同长度的轻弹簧相连，弹簧长度取决于该弹簧连接的2像素点的灰度值之差;依据胡克定律求出中心点受到其8邻域质点的弹簧力合力，如果合力大于阈值就可以判定中心点为边缘线上的点［15］。

1 改进的弹簧－质点模型

通过研究文献［14］发现其所述的弹簧－质点算法存在以下缺陷:第一，将相邻像素点的灰度值之差作为弹簧拉伸后的长度，求解时每式中都有弹簧的新长度减去自由长度这一项，显得繁琐;第二，检测效果显示边缘线条很粗，无法精确提取物体轮廓。从这2点出发，本文提出了改进方案。

对于一幅图像(如图1)，为兼顾处理计算量和覆盖面，研究某中心点P(i，j)及其8邻域(即3×3模板)，并假设:① 连接各质点的弹簧为不同材质，弹性系数k定义为该弹簧所连接2像素点的灰度差;② 各弹簧的自由长度都非常小;③ 水平及竖直连接相邻2点间的弹簧经拉伸后的长度为L。由假设可知:整幅图像中所有弹簧都处于拉伸状态，剪切弹簧(即斜向连接质点的弹簧)产生的弹力与水平、竖直方向的夹角均为特殊角(θ=45°)。这些弹簧的伸长量可分别用L和来近似表示。3×3模板的弹簧力示意图如图2所示。依据胡克定律y=kΔx=k(x－x0)=kL，对中心点P(i，j)列x轴方向的受力方程为

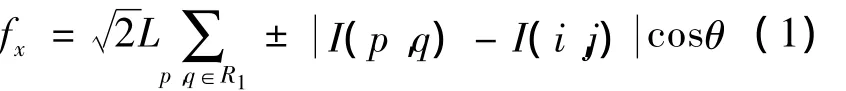
式(1)中:I(i，j)和 I(p，q)分别表示2个像素点的灰度值;R1为8 邻域除去(i，j－1)和(i，j+1)的坐标集(因为位于这2个坐标的质点在x方向没有弹力贡献)，当中心点受力的x轴分量为正时取正号，反之取负。注意到和cos45°总是在剪切弹簧作用时同时出现，并可抵消，故式(1)进一步化简为

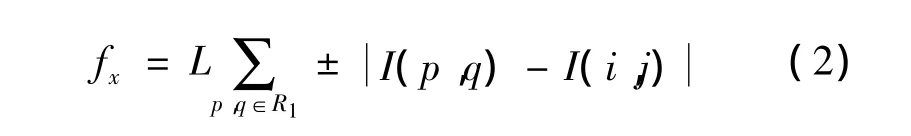
同理，y方向的受力方程为

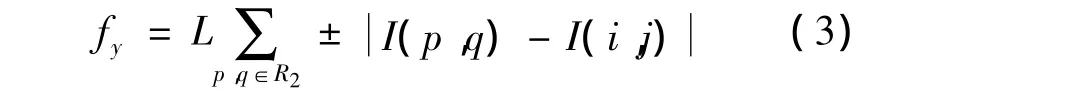
式(3)中，R2为8 邻域除去(i－1，j)和(i+1，j)的坐标集。为了得到更好的检测效果，引入参数C，即:

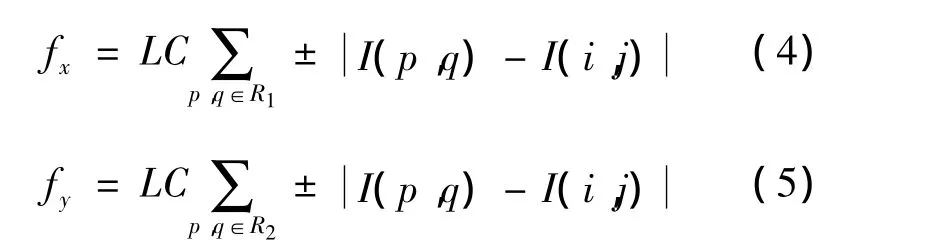
该参数是Etienne等［8］提出的，表达式为

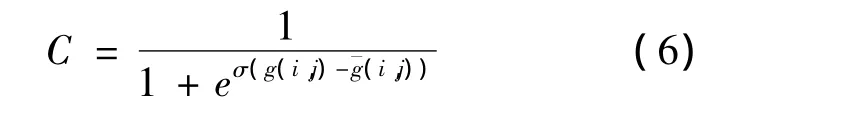
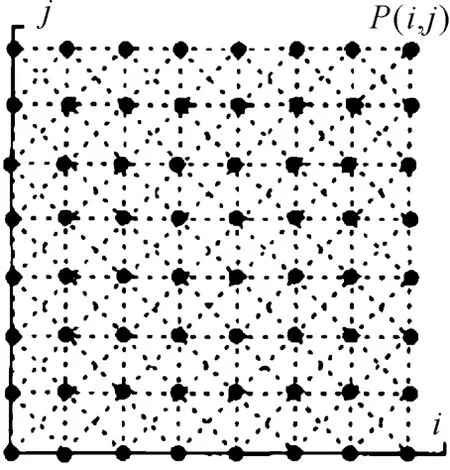
图1 弹簧－质点模型

由式(4)、(5)可知，点 P(i，j)受到的合力及力的方向分别为:

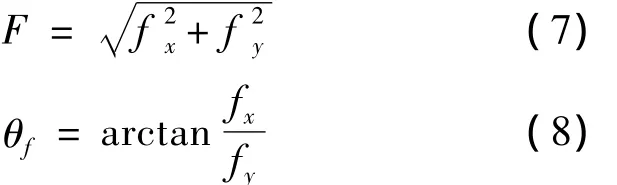
使用最大类间方差法(otsu’s method)时需设定一个阈值。将式(7)的结果与阈值比较就可以确定P(i，j)是否参与构成边缘线。式(8)给出了中心点处边缘线的走向趋势。依照该算法遍历所有像素点，就可以把边缘线条检测出来。图2(a)的中心点左侧受力明显较右侧大，下侧明显较上侧大，因此该中心点所受的合力较大，该点可能为边缘线上的点;图2(b)的中心点受到各方向弹力大小相差不大，合力很小，所以该点不能被检测出来。事实上图2(b)的中心点与它所处的环境反差很大，可能是噪声点。

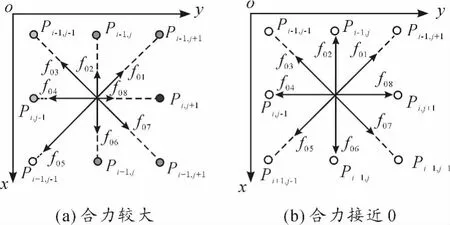
图2 3×3模板的弹簧力示意图

2 实验结果

为证明本文算法的有效性，进行了4组实验:①验证在无噪声情况下，本文算法对图像的边缘检测能力;②把本文算法的结果与文献［14］作比较;③验证在噪声情况下本文算法对图像的边缘检测能力;④测试参数L对算法性能的影响，以便通过调节L来获取最优的边缘检测效果。实验所用的操作系统为Windows 7，程序环境为Matlab R2008b，实验中选取L为0.015，算法中的阈值通过最大类间方差法(otsu’s method)获得。

2.1 无噪声情况

图3为无噪声情况下针对lena图像(图3(a))、肺部CT影像(图3(e))和腹主动脉瘤DSA影像(图3(i))，本文算法与几种经典算法的边缘检测效果。

结果显示:2种一阶算子(图3(b)、(j))都漏检了很多有用的边界;Canny算法(图3(c))的边界连续性稍好，却产生伪边缘而导致人物面部严重失真;LOG算法(图3(k))使血管影像出现了意外的间断。本文算法能较真实地反映原图:图3(d)中人物的眼睛和帽子边缘清晰、连续性好;在图3(h)中肺与纵隔的边界清楚，且脊柱的轮廓清晰完整;在图3(l)中血管的连续性完好。

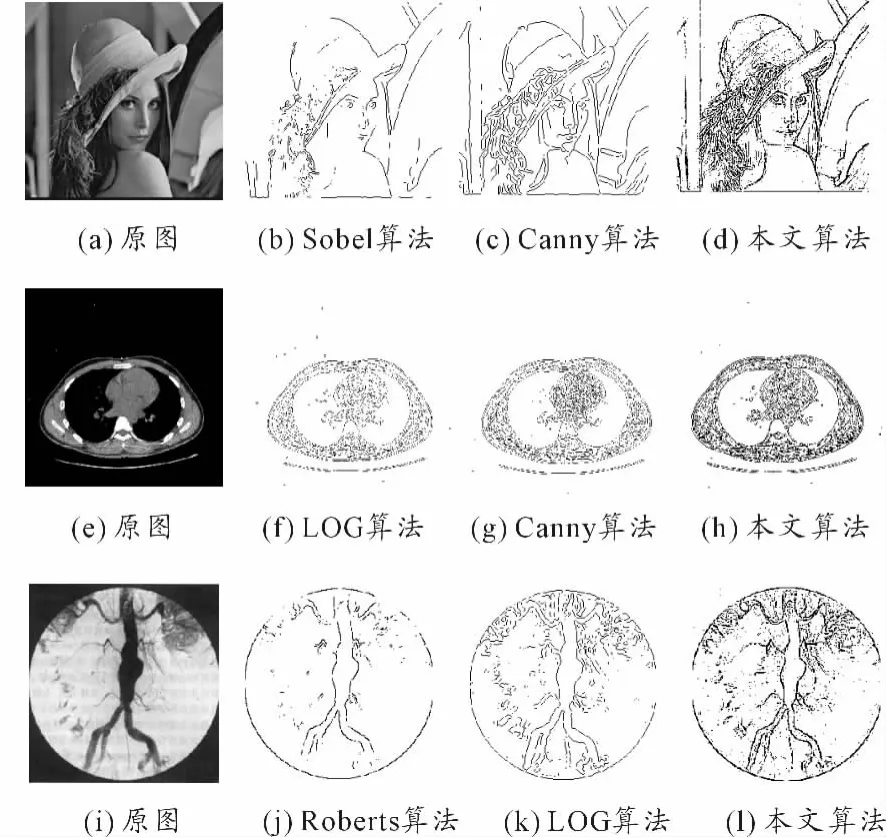
图3 无噪声图像的边缘检测效果

2.2 与弹簧－质点算法对比

为了方便与文献［14］的结果进行对比，需将本文算法处理后的lena图像进行反转。

图4的检测结果表明:采用本文算法检测到的图像边缘线条精细、清晰，效果优于改进前的算法。

图4 与文献［10］对比的检测结果

2.3 噪声情况

图5为噪声情况下(噪声类型为椒盐噪声，强度为0.02)针对北京市地图截图(图5(a))和器皿图像(图5(e))，本文算法与几种经典算法的测试结果。

图5(a)～(d)表明在检测加噪的地图图像时，本文算法检测效果较好。强噪声对边缘检测的结果影响不大，图5(d)中主干道以外的部分小街道仍可轻易识别，地图上的部分文字可以辨认。图5(h)则显示强噪声导致本算法的结果中出现很多矩形小方块，严重影响了整体效果。实际上，在图2(b)中质点的受力示意图表明:噪声点和周围的环境反差较大时质点所受的合力接近0。但相邻点受到噪声点施加的弹力会很大，容易被误判为边缘，这就是图5(h)中出现很多小矩形方块的原因。所以本算法对噪声的滤波作用比较有限。

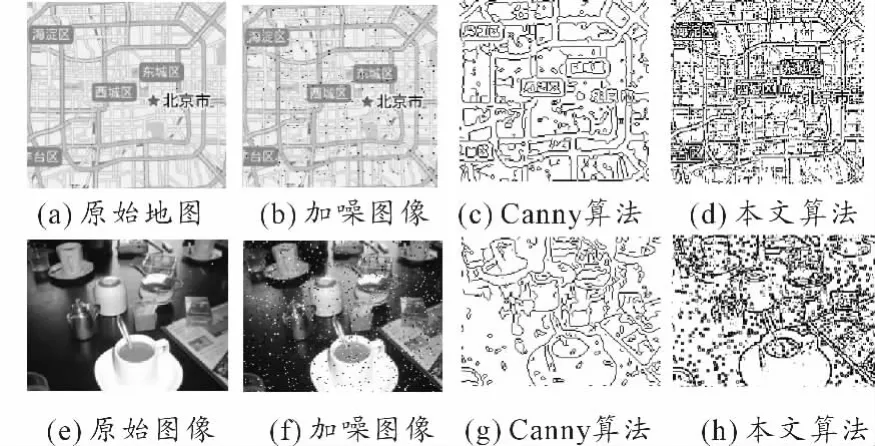
图5 抗噪声测试结果

2.4 参数L的作用

本文算法中弹簧伸长量L是一个很重要的参数，对整个算法的灵敏度具有调节作用。选取lena图像作为检测对象进行研究。图6(a)～(d)展示了当L取不同值时本文算法的检测结果。

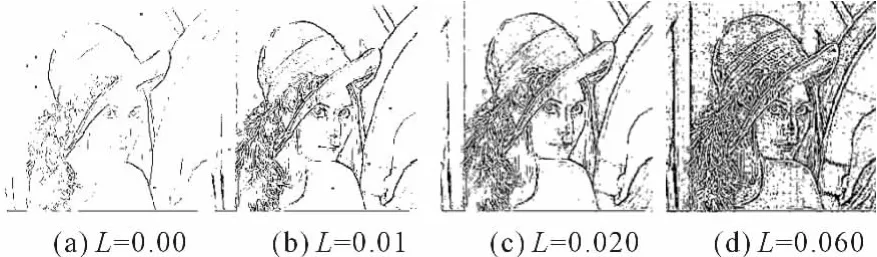
图6 改变变数L对检测结果的影响

结果显示:当L取值增大时，边缘线条也随之变得明显(如图6(a)～(c));但如果L过大则会导致部分背景也被误判为边缘点(如图6(d))。因此，为了达到较好的效果，需要设定合适的弹簧长度L。通过大量实验发现:当阈值使用最大类间方差法计算时，L为0.01～0.03比较适宜。

3 讨论

本文算法的优越之处主要表现在:①原理简单、过程简洁。基本依据是胡克定律，并将弹性系数k视为可变、弹簧长度L视为常量，使计算简化、便于编程。②对于无噪声图像边缘检测效果好。图3中的3组图像对照表明:本文算法既能保持细节处边缘的连续性，又能防止产生伪边缘。③引入2个参数C和L。C加强了中心点与其邻域的联系，使检测效果明显改善;L则实现了对算法灵敏度的调节。

本文算法有以下几点不足:①对图像噪声的处理机制存在缺陷，实际应用中应在预处理过程进行去噪处理。②对于组成整幅图像边界的像素点尚无法进行处理。这些像素点仅受图像内侧点的作用，在外侧无弹簧连接，因此受力不平衡，所以有必要忽略整幅图像最外层的像素点。

4 结束语

本文采用弹簧－质点模型对图像边缘检测算法进行了改进。实验对比结果表明:该算法具有较好的检测效果。若与去噪算法配合使用将能克服自身不足，能在尽量保留原图细节的同时提取到连续性较好的边缘。下一步将在抗噪声方面对本文算法进行研究。

［1］王智文.几种边缘检测算子的性能比较研究［J］.制造业自动化，2012，34(6):14 －16.

［2］任丽莎，贾瑞芝，杨莹.基于特征探测函数的图像去噪［J］.重庆理工大学学报:自然科学版，2011，25(9):43－47.

［3］林旭云.基于二值化增强的边缘检测算法［J］.重庆理工大学学报:自然科学版，2012，26(5):94－100.

［4］张利红，梁英波，支联合，等.基于多结构多尺度形态学梯度的医学图像边缘检测［J］.激光杂志，2012，33(3):31－32.

［5］袁源，樊万梅.基于背景统计的ROI提取方法［J］.重庆理工大学学报:自然科学版，2012，26(3):89－92.

［6］田微晴，朱卫岗，杨顺隆，等.基于相位一致性的SAR图像边缘检测［J］.四川兵工学报，2012，33(9):89－91.

［7］唐晓强，孟庆柏，赖惠成.利用自适应灰度形态学检测噪声图像边缘［J］.激光杂志，2011，32(1):12 －14.

［8］孙军，黎琪，李和睿.基于集合映射的彩色图像边缘检测［J］.四川兵工学报，2012，33(10):86 －87.

［9］Sun G Y，Liu Q H，Liu Q.A novel approach for edge detection based on the theory of universal gravity［J］.Pattern Recognition，2007，40(10):2766 －2775.

［10］Lopez M C，Bustince H，Fernandez J.A gravitational approach to edge detection based on triangular norms［J］.Pattern Recognition，2010，43(11):3730 －3741.

［11］余昌盛，许力.基于弹簧质点模型的织物变形仿真技术［J］.江南大学学报:自然科学版，2005，4(3):261－265.

［12］刘凌霞，宋强.基于简化的质点－弹簧模型织物变形仿真研究［J］.计算机仿真，2011，28(5):406－409.

［13］李健，崔栋梁.基于简化的质点弹簧模型的布料模拟［J］.计算机工程与设计，2010，31(4):819 －821.

［14］徐遥，张如艳，王士同.一种新的基于改进弹簧质点模型的图像边缘检测方法［J］.计算机应用研究，2011，28(4):1573－1583.

［15］Etienne V，Robert L.Detecting and matching feature points［J］.Journal of visual communication and image representation，2005，16(1):38 －54.