巧用割补，化难为易

湖北 全福林

巧用割补，化难为易

湖北 全福林

在组合图形中，除了多边形外，还有由圆、扇形、弓形与三角形、长方形、平行四边形、梯形等图形组合而成的不规则图形。为了计算它们的面积，常常需要变换图形的位置或对图形进行分割、旋转、拼补，使它变成可以计算出面积的规则图形。在多边形的组合图形中，为了计算面积，有时也要用到割补的方法。请看下面几题，相信你会大有收获。

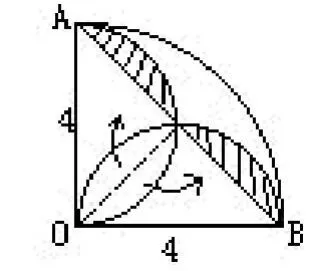
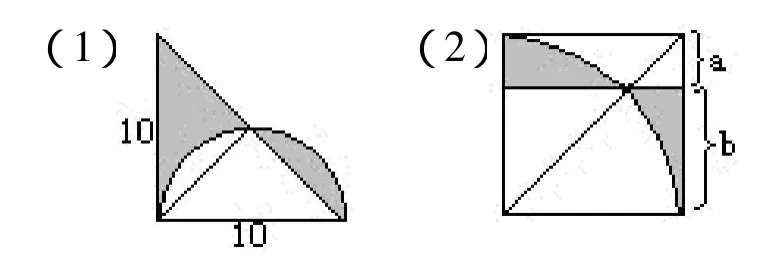
1.求下列各图中阴影部分的面积。

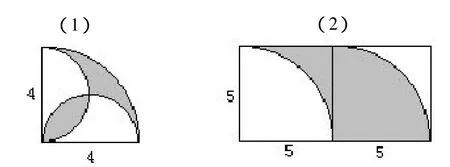
分析与解：（1）如左下图所示，将左下角的阴影部分一分为二，然后按照右下图所示，将这两部分分别拼补在阴影位置。可以看出，原题图的阴影部分等于右下图中AB弧所形成的弓形，其面积等于扇形OAB与三角形OAB的面积之差。（2）在题图虚线分割的两个正方形中，右边正方形的阴影部分是半径为5的个圆，而左边正方形中空白部分也是半径为5的个圆。

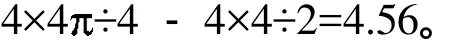
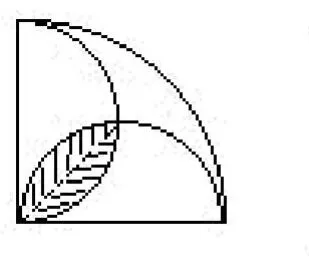
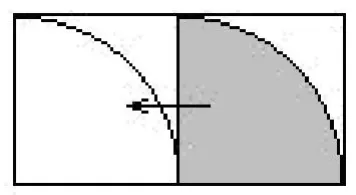
如下图所示，将右边的阴影部分平移到左边正方形中。可以看出，原题图的阴影部分正好等于一个正方形的面积，为5×5=25。

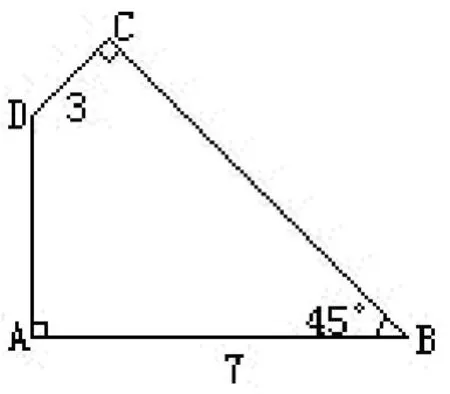
2.在左下图的直角三角形中有一个长方形，求长方形的面积。

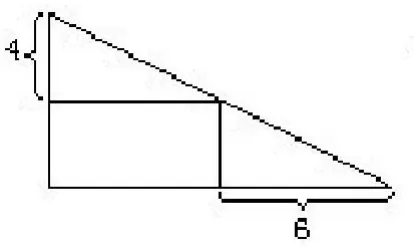
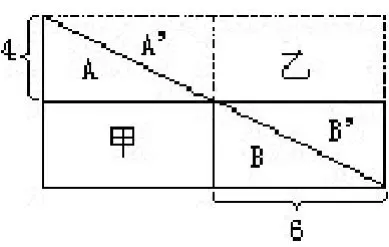
分析与解：题中给出了两个似乎毫无关联的数据，无法沟通与长方形的联系。我们给这个直角三角形再拼补上一个相同的直角三角形（见右上图）。因为A与A′，B与B′面积分别相等，所以甲、乙两个长方形的面积相等。乙的面积是4×6=24，所以甲的面积，即所求长方形的面积也是24。

3.下图中，甲、乙两个正方形的边长之和是20厘米，甲正方形比乙正方形的面积大40平方厘米。求乙正方形的面积。

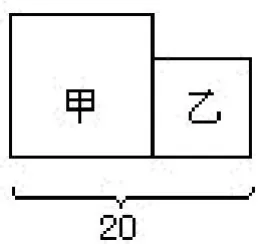
分析与解：如果从甲正方形中“挖掉”和乙正方形同样大的正方形丙，所剩的A，B，C三部分之和就是40平方厘米（见左下图）。

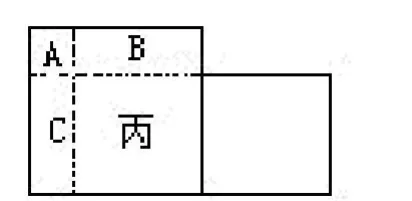
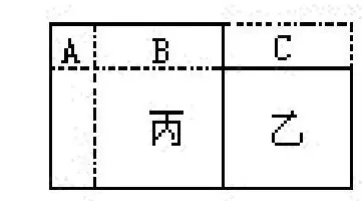
把C割下，拼补到乙正方形的上面（见右上图），这样A、B、C三块就合并成一个长为20厘米的长方形，面积是40厘米2，宽是40÷20=2（厘米）。这个宽恰好是两个正方形的边长之差，由此可求出乙正方形的边长为（20-2）÷2=9（厘米），从而乙正方形的面积为9×9=81（平方厘米）。

同学们，你们学会了将不规则图形转化为规则图形的“移花接木”之术了吗？赶快一试身手吧！

练一练：

1.求下列各图中阴影部分的面积。

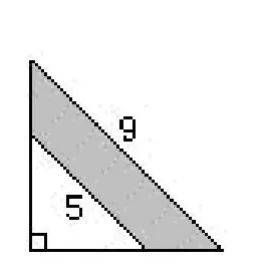
2.如左下图所示，在一个等腰直角三角形中，削去一个三角形后，剩下一个上底长5厘米、下底长9厘米的等腰梯形（阴影部分）。求这个梯形的面积。

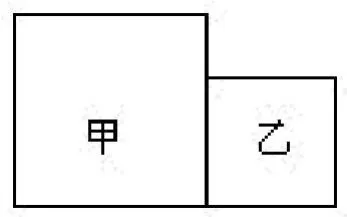
3.下图是甲、乙两个正方形，甲的边长比乙的边长长3厘米，甲的面积比乙的面积大45平方厘米。求甲、乙的面积之和。

4.求下图（单位：厘米）中四边形ABCD的面积。