三维编织物增强复合材料横向冲击频域响应特征
2013-09-17张岩,孙宝忠
三维编织物增强复合材料横向冲击频域响应特征
张 岩,孙宝忠
(东华大学 纺织学院,上海201620)
采用改进型分离式霍普金森杆测试三维编织物增强复合材料在横向(试样厚度方向)冲击加载模式下动态力学响应特征.试验结果表明,最大载荷随冲击速度增加而增加,从试样破坏显微照片中可以得出,随着冲击速度增加,三维编织物增强复合材料失效模式由树脂开裂变为纤维束断裂.采用快速傅里叶变换方法将三维编织物增强复合材料横向冲击时间-载荷曲线转换为频域内频率-振幅曲线,从曲线中可以得出横向冲击应力波频率主要集中于低频区域,且应力波振幅随冲击速度增加而增加.
三维编织物增强复合材料;横向冲击;霍普金森杆;快速傅里叶变换;频域特征
三维编织物由3根或3根以上纱线相互缠绕或正交交错交织而成.三维编织物加强了织物厚度方向的力学性能,因而由其制成的三维编织物增强复合材料在受力时不会像层合复合材料一样出现分层现象.基于三维编织物的整体结构、坚固耐用、设计灵活等特征,三维编织物及其复合材料广泛用于生物医学、航空航天、体育等领域[1].三维编织复合材料在以上领域应用过程中不可避免会受到冲击载荷作用,因此研究其在冲击载荷下的动态力学性能有重要意义.针对三维编织物增强复合材料动态力学性能的研究已有很多[2-7],但这些研究主要集中于时域内,均是在时间尺度上表征三维编织物增强复合材料动态力学响应.本文采用时频转换方法将时间尺度上动态力学特征转换到频域内,在频域内探究三维编织物增强复合材料动态力学性能.
1 三维编织物增强复合材料及测试
1.1 三维编织物增强复合材料
使用日本东丽公司(Toray®)生产的T300-6k碳纤维束,采用四步法1×1编织方法编织三维织物.三维编织物的纱锭分布为29×5,编织角为(28±3)°,节长为(3.2±0.2)mm.常温下,采用树脂传递模塑方法(RTM)将环氧树脂(TDE-85)注入三维编织物.固化工艺:首先在130℃下固化2h,然后升温至150℃固化1h,继续升温至160℃固化8h,最后在180℃条件下固化3h.
最终固化后的三维编织物增强复合材料如图1所示,其尺寸为125mm(长)×25mm(宽)×3mm(厚),纤维体积分数约为58%.

图2 改进型分离式霍普金森杆装置Fig.2 Modified split Hopkinson bar apparatus

图1 三维编织物增强复合材料形态Fig.1 Photograph of 3-D braided fabric reinforced composite
1.2 横向冲击测试
采用改进型分离式霍普金森压杆(如图2所示)测试三维编织物增强复合材料横向冲击性能.该装置由气枪、撞击杆、输入杆和动力捕获装置组成,撞击杆和输入杆长度分别为300和800mm,撞击杆和输入杆及输入杆半球形端部直径均为14.5mm.
改进型分离式霍普金森杆的工作原理如图3所示.根据一维应力波理论,当撞击杆撞击输入杆时,产生一个长度为撞击杆长度两倍的弹性波长,并沿输入杆向前传播.当应力波到达输入杆和试样接触面处时,弹性应力波分为两部分:一部分进入试样内部,另一部分应力波则沿原路返回.沿原路返回的应力波在到达输入杆端部时,因自由面反射,再次变为冲击波沿输入杆传播并撞击试样.这一过程将持续多次直至应力波消散或试样断裂.为了记录应力波传播历史,两个应变片串联后呈180°贴于输入杆中间位置.这种贴法可以尽量避免输入杆在冲击过程中左右扰动引起信号偏差.
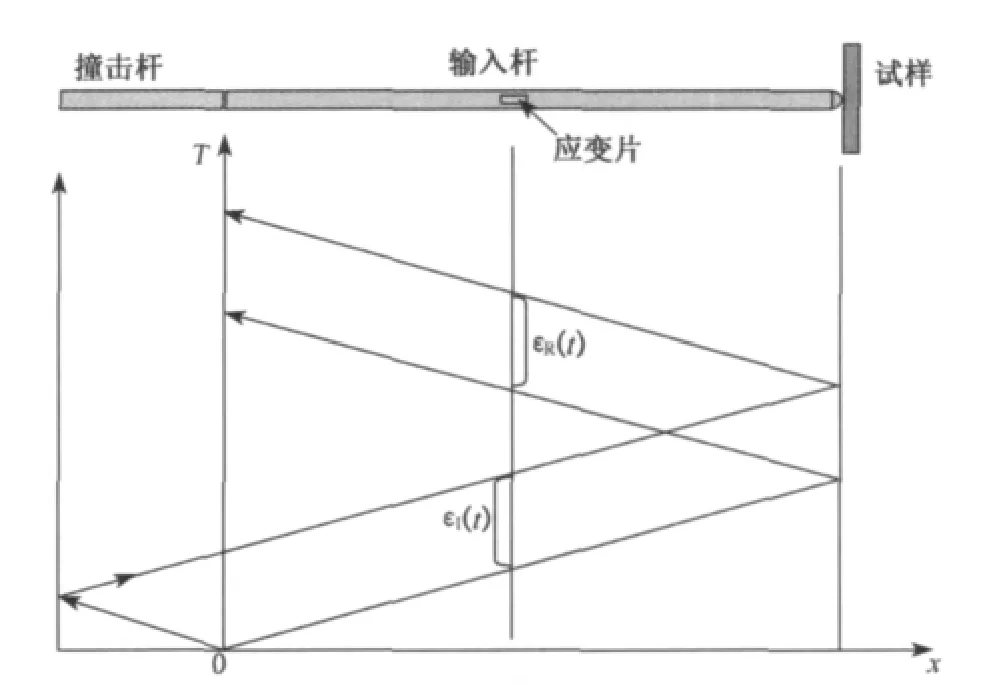
图3 改进型分离式霍普金森杆测试原理Fig.3 Testing principle of modified split Hopkinson bar
横向冲击试验中试样所承受载荷、位移、应力波速度及能量吸收可由式(1)~(4)[8]计算得:
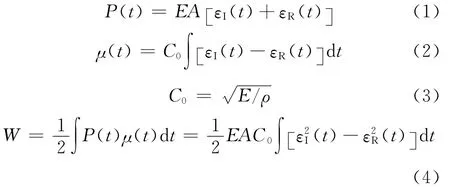
其中:εI(t)和εR(t)分别为应变片采集到的输入脉冲和反射脉冲;E,A,ρ分别为输入杆杨氏模量、横截面积和密度;t为时间.由式(1)~(4)可得试样所受冲击载荷及位移均为时间函数,故可以通过消去时间得到三维编织物增强复合材料载荷-位移曲线.本文采取3个冲击速度分别为13.6,17.8和22.8 m/s,每个速度进行3次重复试验,以得到重复性较好数据.
2 结果与讨论
2.1 动态力学响应
由式(1)~(4)计算得到三维编织物增强复合材料载荷-位移曲线如图4所示.根据分离式霍普金森杆工作原理可知,输入杆会对试样进行多次冲击,所以载荷-位移曲线表现出波动性.由于较高冲击速度拥有更大冲击能量,冲击载荷最大值随着冲击速度增大而增大.在任一冲击速度下,载荷最大值随着冲击次数增加而减小,其随冲击次数的变化如表1所示.经过4次冲击后,在13.6,17.8和22.8m/s 3种冲击速度下,相应的最大载荷分别下降了36.2%,38.7% 和30.9%.图4中同一冲击速度下试样受到单次冲击位移变化如表2所示,随着冲击次数的增加,试样位移逐渐减小.同时也可以观察到试样位移随冲击速度的增加而增加.
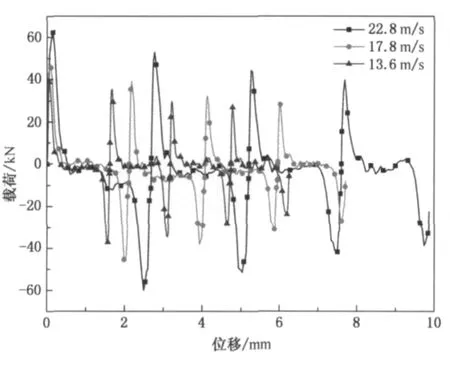
图4 三维编织物增强复合材料横向冲击载荷-位移曲线Fig.4 Load-displacement curve of 3-D braided fabric reinforced composite under transverse impact
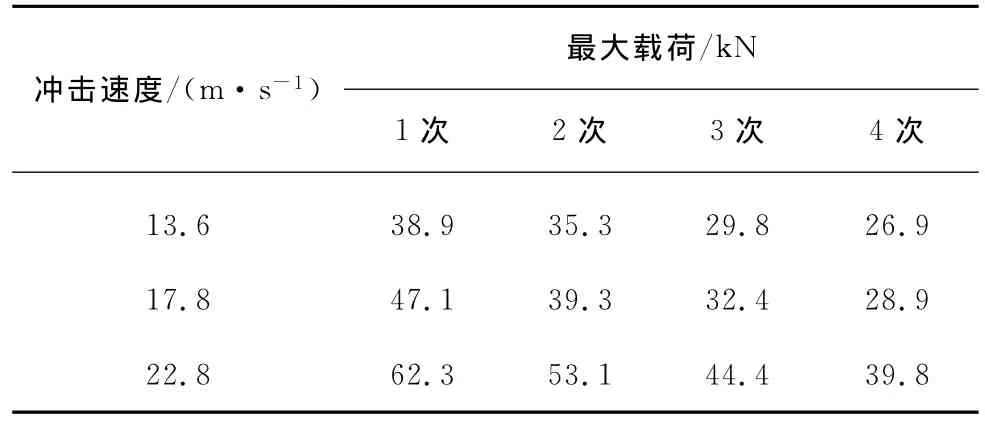
表1 三维编织物增强复合材料在3种冲击速度下的最大载荷Table 1 Peak load of 3-D braided fabric reinforced composite under 3different impact velocities
2.2 破坏形态及失效模式
三维编织物增强复合材料在3种冲击速度下横向冲击加载模式的局部失效形态如图5~7所示.由图5可知,从正面形态中可以看到在输入杆与试样冲击点处有凹坑,为输入杆冲击过程中对试样压缩所致,冲击点附近可以明显观察到树脂裂痕及纤维束与树脂界面脱黏;相比于正面破坏形态,背面形态中只有碳纤维束和树脂基体脱黏引起的微小裂痕.三维编织物增强复合材料在13.6m/s冲击速度下失效模式主要为树脂开裂和纤维束与树脂脱黏.
在17.8和22.8m/s冲击速度下三维编织物增强复合材料完全断裂,所以取一半试样进行观察.由图6和7可以清晰地观察到树脂开裂和纤维束的断裂.可见三维编织物增强复合材料在17.8和22.8m/s冲击速度下的失效模式为树脂开裂和纤维束断裂.


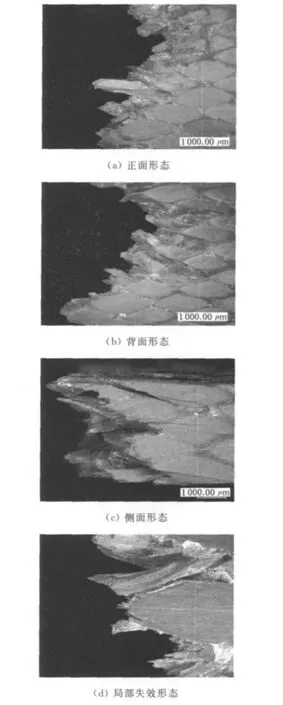
图7 三维编织物增强复合材料横向冲击失效形态(v=22.8m/s)Fig.7 Fracture morphology of 3-D braided fabric reinforced composite under transverse impact(v=22.8m/s)
3 频域响应特征
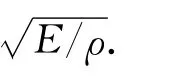
三维编织物增强复合材料横向冲击时间-载荷曲线经FFT变换后得到频率-振幅曲线如图8所示.由图8可知,冲击应力波频率分布在0~200kHz之间,其中振幅较高同时也是冲击能量较为集中部分主要在0~50kHz之间.由此可以看出,三维编织物增强复合材料横向冲击应力波能量主要集中于低频部分.
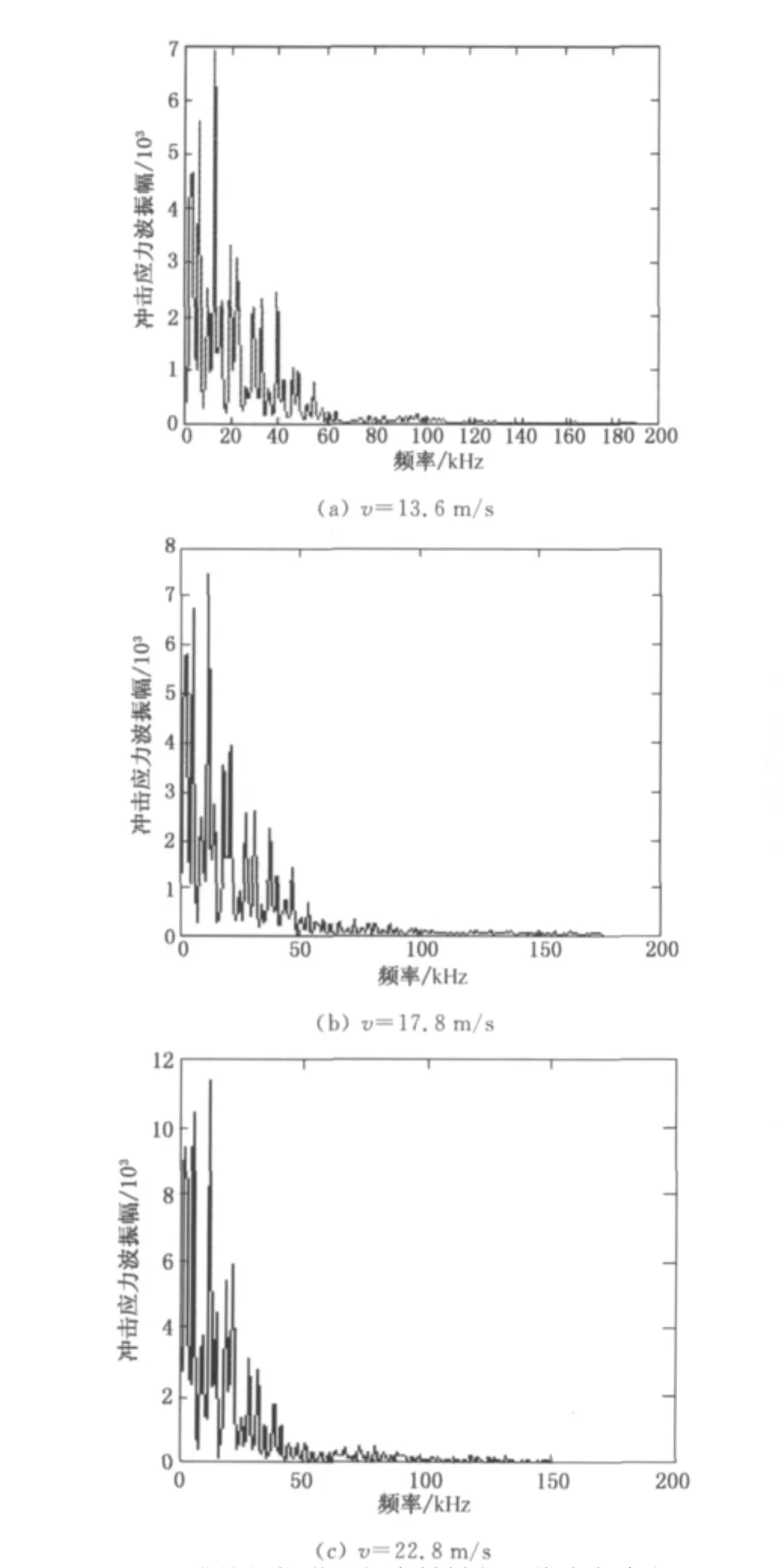
图8 三维编织物增强复合材料在3种冲击速度下频率-振幅曲线Fig.8 Frequency-amplitude curve of 3-D braided fabric reinforced composite under 3different impact velocities
三维编织物增强复合材料在3个冲击速度下局部频率(0~50kHz)特征对比如图9所示.由图9可以看出,随着冲击速度增加,冲击应力波振幅逐渐增加,但振幅最大值对应频率无明显变化.由此可以得出,三维编织物增强复合材料在低速范围内横向冲击加载速度变化对应力波频率几乎无影响,也即三维编织物增强复合材料在3种冲击速度下振动频率相同,但对应力波振幅幅值影响较大.
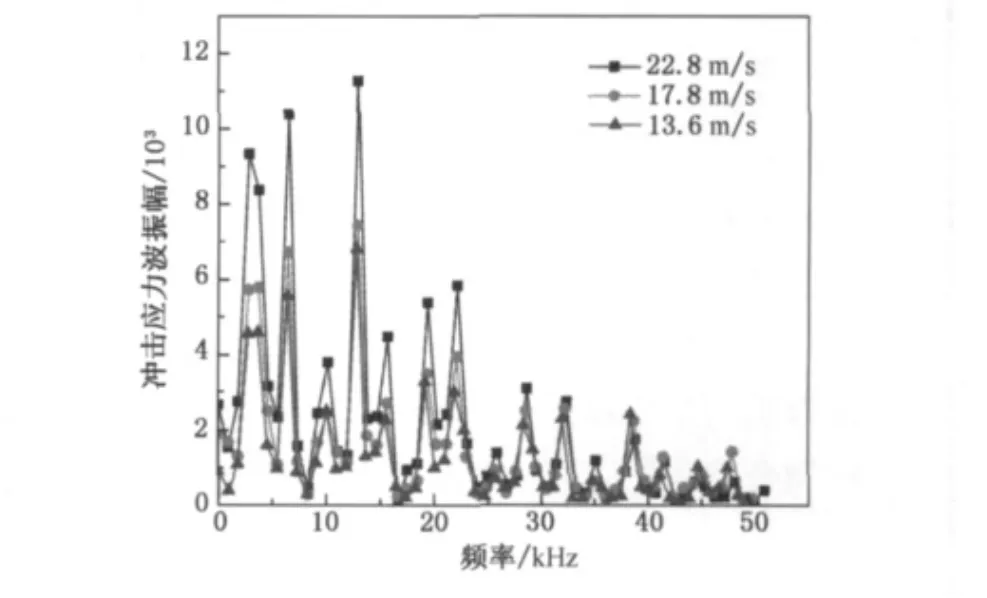
图9 三维编织物增强复合材料在3种冲击速度下局部频率-振幅曲线Fig.9 Local frequency-amplitude curve of 3-D braided fabric reinforced composite under 3different impact velocities
4 结 语
本文测试了三维编织物增强复合材料在横向冲击加载模式下动态力学性能,从载荷-位移曲线中可以看出最大载荷及最大载荷处对应位移均随冲击速度增加而增大.而在同一冲击速度下,最大载荷及其对应位移随冲击次数增加而减小.从破坏形态中可以得出,三维编织物增强复合材料在13.6m/s冲击速度下的失效模式以树脂开裂以及纤维束与树脂脱黏为主,而随着冲击速度增加,失效模式主要表现为纤维束断裂.三维编织物增强复合材料横向冲击时间-载荷曲线经快速傅里叶变换(FFT)后发现冲击应力波频率主要集中于低频段,冲击应力波振幅随着冲击速度增加而逐渐增大,而在3种冲击速度下的冲击应力波振幅最大值对应频率相同.
参 考 文 献
[1]ECKHARD U, PARWIS C. Endocardial carbon-braid electrodes[C]//66th Scientific Sessions of the American Heart Association.Atlanta,US,1993:88.
[2]FLANAGAN M P,ZIKRY M A,WALL J W,et al.An experimental investigation of high velocity impact and penetration failure modes in textile composites[J]. Journal of Composite Materials,1999,33(12):1080-1103.
[3]JENQ S T,MAO J J.Ballistic impact response for two-step braided three-dimensional textile composites [J]. AIAA Journal,1996,34(2):375-384.
[4]JENQ S T,KUO J T,SHEU L T.Ballistic impact response of 3 -D four-step braided glass/epoxy composites[J].Key Engineering Materials,1998,141/142/143:349-366.
[5]SHAKER M,KO F,SONG J.Comparison of the low and high velocity impact response of Kevlar fiber-reinforced epoxy composites[J].Journal of Composites Technology & Research,1999,21(4):224-229.
[6]SUN B Z,LIU F,GU B H.Influence of the strain rate on the uniaxial tensile behavior of 4-step 3-D braided composites[J].Composites Part A,2005,36(11):1477-1485.
[7]SUN B Z,GU B H.High strain rate behavior of 4-step 3-D braided composites under compressive failure[J].Journal of Materials Science,2007,42(7):2463-2470.
[8]MEYERS M A.Dynamic behavior of materials [M].New York:John Wiley &Sons Inc,1994:296-322.
The Frequency Domain Character of 3-D Braided Fabric Reinforced Composite under Transverse Impact
ZHANGYan,SUNBao-zhong
(College of Textiles,Donghua University,Shanghai 201620,China)
The dynamic mechanical response of three-dimensional (3-D)braided fabric reinforced composite under transverse impact was tested with modified split Hopkinson bar.The experimental results showed that the peak load increased with the increase of impact velocity.Based on the fracture morphologies of 3-D braided fabric reinforced composites,the failure mode was changed from resin crack to fiber tows breakage with the increase of impact velocity.The frequency-amplitude curve in frequency-domain can be obtained from time-load curve in time-domain by fast Fourier transform (FFT)method.It can be observed from the curve that the impact stress wave mainly concentrated on the low frequency area and the stress wave amplitude increased with the increase of impact velocity.
3-D braided fabric reinforced composite;transverse impact;Hopkinson bar;fast Fourier transform;frequency-domain character
TB 332
A
1671-0444(2013)01-0037-05
2012-06-21
张 岩(1986-),男,山东东营人,博士研究生,研究方向为三维编织复合材料动态力学性能.E-mail:zhangyan1986@mail.dhu.edu.cn
孙宝忠(联系人),男,副教授,E-mail:sunbz@dhu.edu.cn
