锌电极放电过程及失效机制数值分析

宋 辉 徐献芝 李 芬

(中国科学技术大学近代力学系,合肥230027)

1 引言

由于具有优异的电化学性能,如低平衡电位、高比能量与能量体积密度、储量丰富、成本低廉及对环境友好等,锌材料自电池发明以来一直被广泛采用作为一次、二次电池的阳极材料.如支配助听器市场的锌-空气纽扣电池,在一次电池市场占据主导地位的锌-二氧化锰电池,以及镍锌电池,锌银电池等.据估计锌基电池占有整个500亿美元电池市场的三分之一.1

目前对锌阳极的研究集中在可充式二次电极及机械可再充式.2但二次电极一直受困于两个问题,即在充电过程中锌电极的形状改变和枝晶生长.这些问题阻碍了性能优越的锌镍电池和二次锌-空气电池等的商业化发展,使其目前还主要处于实验室研究阶段.对于二次锌-空气电池而言,它还需要一个双功能的空气电极:在放电时作为正极而充电时作为负极.而机械可更换式锌电极的应用却逐渐在商业上普及开来.机械可再充的定义是:在电池结束放电后,用新的锌阳极替换旧的锌阳极继续工作,旧阳极则被送回电解厂循环再生.目前商业上应用的锌-空气电池基本都采用了这种循环方式.如,1995年以色列Electric Fuel有限公司进行了为期两年的电动邮政车的试运行,在64辆邮政车上采用锌-空气电池电源;32004年,Arotech公司为以色列安全局研制微型无人机使用的锌-空气电池;武汉泓元伟力新能源科技公司于2012年1月研制了首辆锌-空气电池纯电动城市公交客车.2012年初,台湾屏东科技大学研制了一辆采用锂离子和锌-空气电池作为混合动力的电动汽车.这些项目的开展也表明了锌-空气动力电池研究的迅猛发展以及良好前景.

在电池领域中,研究方法以实验为主,它可以提供电池系统最直观真实的数据,帮助研究者了解电池的工作机理.借助于实验可以测试包括电极制作工艺、电解液成分、电极添加剂、电极材料特性(如孔隙度、颗粒度)、催化剂含量等多个因素对电池性能的影响,从而获得关于电极优化设计的可信数据.如欧秀芹和梁广川4研究了烧结工艺对于气体扩散电极性能的影响;李芬等5从多个角度研究了提高气体扩散电极输出功率及延长电极循环使用寿命的方法.李思振等6研究了电解液中添加Carbopol树脂以及电极中添加Bi对锌电极电化学行为的影响.但一般情况下,电池是一个封闭的体系,内部由电解液及电极材料填充,电极材料一般也为多孔结构,导致很难通过实验方法直接测量其内部物理量的分布,尤其是实时变化的测量,从而很大程度上影响了研究者对于电池运行规律的认识.在这种情况下,数学模型提供了一个很好的选择.只要模型、参数及边界条件选择建立恰当,其结果就可以准确地模拟电极内部的物理化学过程.相对于实验研究,数学建模成本较低;其建模过程也有助于了解电极运行规律.

锌电极的运行涉及多个物理化学过程,包括物质传递、电化学反应、异相化学反应等,相应地其反应机理非常复杂.这在一定程度上也促进了数学模型的应用.Choi等7针对二次银锌电池建立数学模型,分析了电池的形状改变,充电过程中活性材料的重新分配等.数值计算表明电极的形状改变主要是由电极内部的对流引起的,消除对流可以有效地改变这一问题.Sunu等8,9通过建立一维数学模型研究了圆盘多孔锌电极在放电过程中多个物理量如锌、氧化锌的体积分数,离子浓度,交换电流密度等的分布变化以及过电位的变化.并对电极的失效机制进行了深入探讨.数值结果显示电极反应高度不均匀,反应区域靠近电极表面,且非常薄.在放电后期固体氧化锌的大量析出会造成电极的孔堵塞,进而引发失效.该实验及理论模型揭示了锌电极过程的基本规律,为后来的研究者认识及设计锌电极提供了非常大的帮助.Isaacson等10建立了二维模型以模拟可充式镍锌电池在二次和三次循环过程中的不均匀性电流密度分布,Zn与ZnO的重新分布,及氧化锌溶解-析出对电极性能的影响.由于循环使用的需要,模拟中设置的电极最大放电容量只相当于实际容量的1/3,放电电流密度也较小,加之假设电极孔隙度为常数,因而该模型只适用于模型小电流下镍锌电池的循环过程.Podlaha和Cheh11基于Sunu的模型建立圆柱形锌锰电池的全电池模型,以模拟高放电速率下的放电规律.与实验结果的比较显示考虑氧化锌在隔膜中析出过程的模型最符合实验结果,这说明了研究锌酸根离子浓度分布的重要性.模拟表明隔膜堵塞是电极失效的最主要原因.另外作者对多个电极参数进行了敏感性分析,表明隔膜的孔隙度及初始氢氧根离子浓度对电极性能有重要影响.Mao12通过建立一维数学模型模拟了一次锌-空气电池的放电过程,考虑了空气电极与隔膜内的离子浓度分布.其结果显示阳极材料利用率受氢氧根离子损耗的限制;相对于孔隙度,电极厚度对材料利用率的影响较小;增大电极活性材料的装载量会降低电极材料的利用率及放电容量.Venkatraman和Vanzee13针对银锌电池建立了一维数学模型,重点研究了放电过程中反应前沿在锌电极中的推进.该模型认为锌酸根离子的浓度远小于氢氧根离子因而不予考虑.相应地也没有考虑锌酸根离子-固体氧化锌的溶解-析出异相反应,这个原因造成模拟结果中电极孔隙度的改变很小.实际上在放电过程中锌酸根离子的浓度相对初始浓度会增加很多,而氢氧根离子的浓度将持续减少,因而锌酸根离子浓度不再是可忽略的;而锌酸根离子及溶解-析出异相反应对于分析电极的失效机制具有极其重要的作用,因而建模中的忽略会带来一定的误差.Torabi和Aliakbar14针对银锌电池讨论了电池建模技术,建立了一个一维的单域(single domain)数学模型,模拟了短时间内(300 s)电极内部的物理量分布及电池对间断式电流的响应,并针对电极参数(电解液浓度、传递电流密度)进行了敏感性分析.

以上各个数学模型模拟的都是一次或二次电池,电池的放电电流及容量都较小,而目前工业设计中普遍采用的机械可更换式锌电极具有与一次、二次锌电极不同的技术特点.它的使用方式类似于一次电极,用完即更换,没有充电过程;工作方式类似于二次电极,工作电流密度较一次电极显著增加.但其容量一般比二次电极更大,多用做动力电源.这种大电流大容量的特性决定了机械可更换式锌电极呈现出不同于一次,二次电极的放电规律.

锌基电池的工作电流对电池效率的影响非常大.章小鸽15比较了AA碱性电池的放电容量,发现当放电电流从0.1 A增加到1 A时,放电容量从2.5 Ah降低到1 Ah,只相当于理论容量的30%.这说明电流的变化使电极内部的放电规律发生了重大变化.另外实验表明电极容量的增加也会导致电极材料的利用率显著下降.可见研究大容量大功率工作条件下锌电极的放电规律及其失效机制对于提高锌基电池的性能具有重要的意义.虽然对于锌电极的放电过程,已有理论模型及实验结果9,16都显示,传递电流密度高度不均匀引发局部的固体氧化锌大量析出,造成局部氢氧根离子耗尽是导致锌电极失效的主要原因,但目前对于大容量锌电极在大功率下的放电规律还未见深入的研究,如大电流下电极内部的电流密度分布规律,氧化锌的生成规律,其对质量传输的限制作用等.

本文针对锌电极的放电过程建立了一维数学模型,通过数值方法模拟多个物理量,如离子浓度、电流密度、孔隙度、固体氧化锌体积分数等在电极内部的分布变化.研究高电流密度下锌电极的的放电规律及失效机制,并讨论其设计优化.

本文所采用的数值算法有别于传统电池领域广泛使用的BAND(j)程序,而是在分析控制方程组中各方程数学性质的基础上将其解耦求解,从而提高了计算效率.

2 数学建模

在锌-空气电池的放电过程中,Bockris等17跟据实验提出了碱溶液中锌的反应机制:

其中第三步是整个反应的速率决定步.

根据Butler18测定的平衡常数,Boden等19总结认为,在电解液中只有锌酸根离子的浓度是稳定的、可估量的,其它几种锌的化合离子浓度都非常小.这一结论已被其它研究者所证实.因而所研究的溶液体系中只包含三种离子:Zn(OH)42-、OH-、K+.

在本文中,采用如下的锌电极过程:

反应(1)是电极的电化学反应式,反应(2)描述了溶液中的锌酸根离子与固体氧化锌相互转化的异相反应.

为方便数学描述,以上两个方程可以分别写成一个一般形式的化学计量方程(stoichiometric equation):

其中,Mi表示反应物或生成物的化学式,si、si*分别表示其在化学反应(1)、(2)中的计量系数,如s1=−s1*=−1,s2=4,s2*=2.而zi为其电荷数,n表示电化学反应中传递的电子数,对于电极反应(1),n=2.

放电过程(1)使锌溶解到碱液中,生成锌酸根离子,当锌酸根离子继续聚集以至于其浓度超过平衡浓度后,将失水析出成为固体的氧化锌.氧化锌在电解液中的作用是双重的:一方面,在电解液中加入一定量的氧化锌可有效地阻止锌电极的自放电行为;另一方面,随着电极放电氧化锌固体会逐渐析出,有可能包裹锌颗粒发生钝化,从而造成电极性能下降甚至失效.

锌-空气电池中锌电极的结构示意图如图1所示.图中的CA、CB分别表示本体溶液中的锌酸钾及氢氧化钾的浓度,Φ、i分别表示电势及电流密度,其下标1、2分别表示电子相与离子相.CAS、CBS表示电极内部固/液反应界面上的离子浓度.该表面浓度与本体溶液溶度有一定的差别.

电极底部是一层集流体,一般为高导电性的金属,负责将电子引出电池.在x=0到x=L之间是锌颗粒组成的多孔结构的锌电极,在凝胶剂的作用下它们分散在KOH溶液中.锌电极上层是一层薄膜,然后是薄薄的一层空气电极,空气电极的厚度一般极小.电池放电时,锌电极内部的锌颗粒与表面的碱液发生反应,溶液中的离子在反应点与本体溶液之间发生质量传递.在溶液中,带电离子的定向移动形成离子电流;锌颗粒之间电子的定向移动形成电子电流.

本文建立一个一维的多孔结构的锌电极数学模型,以预测锌电极的电极行为.本模型研究锌电极放电过程中电极内部发生的以下物理/化学过程:(1)放电过程中溶液内部离子的质量传递过程;(2)氧化锌/锌酸根溶解-析出的异相反应;(3)电极反应过程中的锌材料消耗;(4)电极多孔结构的变化规律;(5)电极内部电流密度的分布.

模型基于以下假设:(1)双电层的厚度一般为纳米量级,远小于毫米量级的电极厚度,所以可忽略双电层效应;(2)锌电极在常温下运行,其温度变化在几十度的范围内,不会显著影响电极性能,因而本文不考虑电池内部的温度变化.(3)多孔锌电极中由于加入了聚丙烯酸钠等凝胶剂,在放电过程中不会产生宏观流动,固忽略对流作用.

模型中对多孔介质的描述采用与渗流力学20相同的连续介质方法.即定义多孔介质的特征体元ΔV*,该特征体元的体积比单个孔隙的容积大得多,包含足够数量的孔隙,使其不受孔隙间微观差异的影响;另一方面,它必须比整个研究区域的尺寸小得多,这样才能代表其所处点的物理量.这种定义方法允许我们将所研究的多孔介质视为连续介质,从而其内部各点的物理量是连续分布的,为各物理量的微积分运算提供了理论基础,使我们可以借助于微分方程这个有力的工具来描述电池内部的各种物理化学过程.

2.1 物料方程

根据Fick第二定律,我们可以将电解液中的物料守恒方程表示如下:

其中ε为锌电极的孔隙度,为时间和位置的函数;下标1、2分别代表 Zn(OH)42−、OH−离子.Ci表示离子浓度,Ni表示离子流量.∇为哈密顿算子.Ri代表了电化学反应(1)及溶解-析出反应(2)对于物质生成/消耗速率的贡献.可以表示为

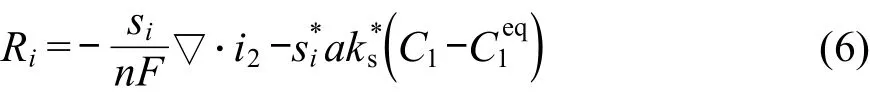
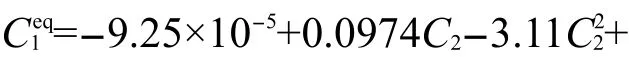
图1 锌电极结构示意图Fig.1 Structure diagram of zinc electrode

带电离子的流量可表示为

其中,上标A、B分别代表锌酸钾(K2Zn(OH)4)和氢氧化钾(KOH).zi是第i种离子的化合价,Di是扩散系数,D1、D2分别表示锌酸钾、氢氧化钾在电解液中的扩散系数.vji代表第j种化合物的一个分子中所包含的第i种离子的个数.由于锌酸根离子只包含在锌酸钾(A)分子中,而氢氧根离子只包含在氢氧化钾(B)分子中,因而为了表述方便可以将vij简写为νi.F为法拉第常数;ti为离子的迁移数;为初始时刻第i种离子的迁移数(transference number);τ为电极的迂曲度.

在多孔介质中,物性参数需要进行修正.如对于一个物性常数,如电导率、扩散系数等,其有效值一般由Bruggeman修正表示为

在溶液中,带电离子的定向移动形成离子电流,即

将流量表达式带入物料守恒方程中,我们得到如下的方程:

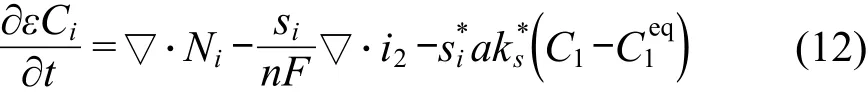
在电极内部双电层之外,电中性假设很好地描述了电解液中各种离子浓度之间的关系:

2.2 固体骨架中的欧姆定律

固体骨架中,电子在电势梯度的作用下形成电子电流.这一过程可用欧姆定律表示为:

其中,εm为电极中导电材料的体积分数,I为电极输出电流密度.固体骨架的导电率可由固体组分有效导电率的加权平均得到:

其中,σZn、σZnO分别为锌金属及氧化锌的导电率,εZn、εZnO分别为其体积分数.

2.3 溶液中的欧姆定律

在溶液中,离子电流不但受到电势梯度的影响,还与溶液中物质的化学势梯度有关.可以用修正过的三相溶液体系中的欧姆定律表示:23

其中,κ为溶液的电导率.KOH溶液的电导率采用如下经验公式:11

μi为第i种物质的化学势.根据Mao:12

其中,γA、γB分别为物质A、B的平均活度系数,假设其与电解液浓度无关.

同前一节一样,此处的电导率也做了修正,使其适用于多孔结构的锌电极.

2.4 电化学速率表达

发生在固-液界面上的电化学反应(1)可以用Butler-Volmer方程来描述,伴随反应发生的还有离子从锌颗粒表面的反应点(reactive sites)向本体溶液(bulk solution)的扩散,或反向扩散.

Podlaha11在对一次性Zn-MnO2电池的建模中,针对锌阳极的电极过程基于Bockris17的数据对各项指数进行拟合,得到采用如式(20)的Butler-Volmer方程.该模型考虑了锌酸根和氢氧根的局部传质过程,本文采用它描述锌电极过程.

式中,j为单位面积的锌活性表面上所产生的电流密度,单位为mA·cm−2.ia,ref为在参考状态下测量得到的交换电流密度.各项指数表征了电流密度对于浓度的依赖性.αa和αc分别为阳极反应和阴极反应的传递系数.

电荷守恒要求:

其中,am为单位体积电极中固-液界面上电极反应的反应活化点的面积.

在电极表面,反应物离子在锌颗粒表面的活化点位置与本体溶液之间存在一个局部的微观质量传递过程.为描述这一过程,我们定义一个特征厚度为δ的质量传递边界层,在此边界层内,反应物的浓度由表面浓度增加/减小到本体溶液中的浓度Ci.这二者之间的关系可以由下式决定(一维):

其中,x为电极厚度方向的坐标,ki为第i种物质在此局部微观传递过程中的质量传递系数.

2.5 固体材料的物质守恒

在锌电极的固体结构中,随着电极反应以及溶解-析出反应的发生,锌会溶解到溶液中,而固体形态的氧化锌会析出.这些固态物质的量的变化会引起电极孔隙度的变化,这一过程可以描述为:

式中,右边第一项表示随着电极反应的发生金属锌逐渐减少,从而电极孔隙度增加;第二项表示随着溶液中锌酸根析出为固体氧化锌,电极的孔隙度逐渐减小.其中VZn,VZnO分别为锌及氧化锌的偏摩尔体积.同样地,我们可以描述金属锌的消耗及氧化锌的生成过程:

在方程(23)中我们没有考虑固体锌酸钾的析出.一般来说,固体锌酸钾的析出几乎是瞬时的,它会很快地溶解到溶液中或者进一步析出为固体氧化锌.在溶液中OH-损耗严重的情况下,锌酸钾固体可能会大量析出,但此时电极早已由于钝化失效.

上面建立的六个方程:浓度守恒(5)、电子电势方程(14)、离子电势方程(16)、Butler-Volmer方程(20)、孔隙度方程(23),构成了一个封闭的非线性微分方程组.包含六个未知函数C1、C2、ϕ1、ϕ2、i2、ε,每个都是时间t与坐标x的函数.其中电子电势方程(14),离子电势方程(16),Butler-Volmer方程(20)的耦合最为紧密,它们描述了电极内部的电流-电势本构关系,为了方便起见我们将其合称为Butler-Volmer方程组(Butler-Volmer equations).

2.6 初始条件与边界条件

初始时刻,浓度均匀分布,即Ci(t=0)=Ci0.

在x=0处,由于集流体的存在,此处溶液的流量为零.由于电流从集流体中引出到外电路,同时有i1=I,即i2=0.由于集流体的存在,此处离子的流量为零,即Ni=0.

在x=L处,离子流形成的离子电流从空气电极经隔膜流入锌电极,所以此处有i2=I,相应地,ia=0.离子可以与隔膜内的离子交换,所以其流量在边界上连续.电势的边界条件可以通过电流的边界条件导出.锌电极内的离子可以与隔膜内的离子交换,所以其流量在边界上连续.此处假设在隔膜内离子浓度保持为初值,这是一个较理想的条件,相当于认为锌电极内的溶液可以不断从边界上获得补充.具体表达式为

其中各个物理量的上标b表示边界上的值,与隔膜的性质有关.d可取为隔膜的厚度.

另外,需注意 Butler-Volmer方程组(14)、(16)、(20)三式的性质.电势的绝对值没有意义,这一性质也反映在这三个方程中.明显地,电子电势与离子电势同时加减一个常数C后得到的新电势值仍然满足这三个方程.所以若不对电势的边界条件进行改进,那么进行数值求解时得到的系数矩阵将是奇性的.此处我们通过规定电子电势在边界上的值解决这一问题.

综上,我们有如下的初始及边界条件:

2.7 数值求解

John Newman于上世纪60年代发布了著名的BAND(j)程序,用来求解电池/燃料电池系统的数值模拟问题.该程序实质上是用Gauss消元法求解用有限差分方法离散得到的代数方程组,然后使用牛顿方法求解对应的非线性问题.至今仍有不少文章使用该程序来模拟电池系统.但从计算效率方面来说,该程序所采用的算法还需加以改进.该算法对方程组统一耦合求解,这对计算机的内存有一定的要求.假设对于一维问题计算区域分为N个网格点,那么耦合求解在每一个迭代步需要求解6N×6N的jocobi矩阵,当计算区域较大或网格分布较密时,这一过程将消耗大量的计算资源.解耦求解则可以有效地降低计算资源的需求.

Um24和Wang25等曾对电池/燃料电池系统的方程组进行归类,参考流体力学中的雷诺输运方程而将方程都写成相似的形式,进而利用CFD中的成熟算法进行求解.

本文对锌电极数学模型中各个方程的数学性质进行分析,将其分为三个子方程组进行解耦求解以提高求解效率.分别为,将描述电流−电势关系的Butler-Volmer方程组耦合求解,描述浓度演化的两个方程(5)与描述孔隙度变化的方程(23)分别独立求解.

采取有限体积方法(FVM)离散控制方程组.有限体积法,或者称为有限容积法,基本思想是在一个个“控制容积”内对控制方程进行积分,以此导出离散方程26,27.其优点在于导出的离散方程仍具有守恒特性,离散方程系数的物理意义明确.在处理边界条件时,采用附加源项法(additional source term method)可以利用统一模式来处理三类边界条件,缩小计算区域,减小计算量.方便了程序的编制,也节省了计算时间.

对于非稳态的浓度方程(5)和锌消耗方程(23),采用隐式格式离散,将方程中的非线性项线性化后求解.在每一时间步的求解中采用预估-校正格式(predictor-corrector).在实施中,可以规定校正的次数:

1≤m≤M

或者规定校正终止的条件:

其中,上标n表示时间步,m表示校正次数.

采用MINPACK28软件包求解Butler-Volmer方程组离散后得到的非线性代数方程组.该软件包采用全局收敛算法搜索方程的根,克服了Newton方法局域收敛的缺点.

本文的计算程序采用Fortran语言编写.在计算中时间步长的调整是一个自适应过程,会根据收敛情况自动增减,规定其最大为30 s,最小约0.05 s.程序使用intel的编译器ifort在Linux平台下运行.测试结果表明,采用全耦合算法的程序求解一个时间步的变量平均约需7.48 s,而本文采用的解耦算法只需1.80 s.其中求解Butler-Volmer方程组的non-Solver子程序占用了绝大部分的cpu时间,这反映了这几个子问题的计算特点,也验证了本文将电极方程组解耦求解是合理的.全耦合算法没有考虑子问题自身的特点而将其耦合求解,一方面相当于将求解浓度,孔隙度/体积分数与求解Butler-Volmer方程组同等对待,增加了大量不必要的计算;另一方面由于方程阶数的增加而导致求解难度增加,所用cpu时间急剧增加,这两方面的原因导致了全耦合算法的效率远低于解耦算法.

图2 算法流程图Fig.2 Flowchart of the algorithm

本文计算程序的算法流程图如图2所示.

3 模型可靠性分析

为验证本文模型的可靠性,我们将数值结果与实验数据进行比较.

图3显示了数值模拟得到的电极过电位曲线.其参数为孔隙度ε=0.73,电极厚度L=0.4 cm,工作电流密度为I=50 mA·cm−2.图中的过电位曲线明显可以分为4个区域.区1显示了当电池刚接通时,有一个瞬间的过电位产生,约8 mV左右,这主要是由电极的活化极化造成的.随后为一个非线性上升区2,这是电极内的物质传输由初始态向准稳态过度引起的.此后电极内的物质传输趋于一个“稳态”,过电位开始随时间线性增加,即区3.随后由于电极内固体氧化锌引起的钝化,过电位开始迅速增加(区4),按照这一趋势,电池电压将很快下降至无法正常工作的状态,因而可视为电极失效的标志.从过电位曲线也可以看出,锌电极在整个运行过程中性能都非常稳定.

图3 锌电极过电位(η)随放电深度(DOD)的变化Fig.3 Overpotential(η)of zinc electrode as a function of depth of discharge(DOD)

图3 与章小鸽测量电流密度为20 mA·cm−2的凝胶锌粉电极得到的数据15曲线规律非常相似,只是由于电极参数的差异而在具体阶段各有不同.这也从一个方面说明了本文数学模型的有效性.

章小鸽15测量了将5 mm厚的锌电极5等分之后不同部分的电流变化.为比较,我们对ε=0.73,L=0.6 cm的电极进行模拟,同样将其5等分,计算不同部分的电流.比较结果如图4所示.可以看出,两个子图的前半部分趋势非常相似,电极开始放电后大部分电流来自于电极靠近表面的第一部分.随着放电的继续,第二部分的电流开始逐步增加,而后三个部分的电流较小.这说明后面几部分的锌直到放电后期才开始溶解.不同的是,实验数据中在放电后期后三个部分的电流开始有较显著的增加,而模拟中其电流一直非常小.这种差异应与电极的各种参数以及边界条件有关.在放电后期,电极内部准稳态的物质传输已经被破坏,参数、边界条件的差异对于电极性能的影响变得越来越明显,决定了电极内固体氧化锌的聚集程度及其后的电极失效方式.部分表现为电极内不同部分的电流变化.

从以上比较可以看出,本文的模拟结果反映了锌电极的基本放电规律,表明了模型的有效性.可以预见,若能够获得实验电极的各确切参数值,本模型的计算结果应与实验结果符合良好.另外在下一节的结果分析中也有多处与已有文献结果的比较分析,也可作为佐证.

4 数值结果分析

4.1 放电规律及电极失效机制

本节讨论锌电极放电的基本规律及其失效机制.首先对电极参数进行说明.电池用多孔锌电极的孔隙度一般在50%−80%之间.电极工作电流密度随用途而变化,一次性电池工作电流一般很小,而动力电池的电流密度则较大,约50 mA·cm−2.计算程序设定最大放电深度为80%,模拟中很少有电池能达到此值.一般计算中如果电极过电位开始急剧增加,则表明电极已不能提供稳定的电量,接近失效,计算中这种情况也设定为终止计算的标志.

图4 锌阳极不同部分电流计算值与实验数据15的比较Fig.4 Comparison of currents of different parts of zinc electrode between simulation results and experimental data15

本文数学模型模拟的物理量包括过电位,锌酸根及氢氧根离子的浓度,电极内部传递电流密度,电极孔隙度,金属锌及固体氧化锌的体积分数等.

电极的过电位定义为集流体侧电极过电位与电极表面过电位之差,即

放电深度(DOD)在一定程度上比放电时间更能反映电池的放电状态,定义为电池已释放容量与其理论容量之比,对于本文中的电池,可表示为:

我们分析参数为孔隙度ε=0.73,电极厚度L=0.4 cm,工作电流密度I=50 mA·cm−2的电极内部各物理量的分布变化,以此模拟电极的放电性能,并在此基础上分析电极的失效机制.

图5显示了锌酸根离子在电极内部的浓度分布变化.可以看出,在10%的放电深度内锌酸根浓度迅速增加,而在随后的放电过程中逐渐减小.这一变化趋势与Sunu8,9及Mao12等的预测相同.其原因在于,在10%的放电深度之内,由于电极反应的持续发生,锌酸根离子大量生成,而同时氢氧根离子的浓度还保持在一个相对高的水平;随后,由于反应的消耗,氢氧根的浓度开始下降;相应的锌酸根离子的平衡浓度的降低以及氧化锌固体的析出使锌酸根离子的浓度开始逐渐下降.对于不同的电极,由于具体参数的差异,锌酸根离子浓度变化的“拐点”发生的具体放电深度也不同,但规律相似,即锌酸根离子的浓度会先到达一个顶点,然后开始下降.对于此处模拟的电极,此拐点发生在10%DOD之前.

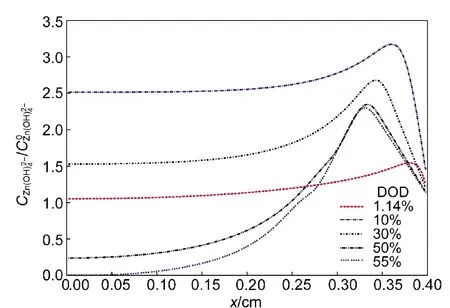
图5 不同DOD时锌酸根离子的浓度分布Fig.5 Distribution of zincate ion concentration at different DOD

图6 是氢氧根离子浓度分布图.从图中可以看到,由于放电过程的持续消耗,且在电极内部越靠近集流体的区域内电迁移作用越弱而导致补充不充分,在电极内部氢氧根离子的浓度不断减小.由于氢氧根离子在锌电极/隔膜界面上可以获得快速的补充,在该界面附近其浓度始终维持在一个较高的值上.

图7是电极内部的传递电流密度的分布图.在放电初期(1%DOD),电流密度在靠近电极表面非常的狭窄区域中远大于其它部分;随着放电过程的继续,这部分区域的锌逐渐消耗,相应地,氢氧根离子的浓度及电导率逐渐降低;而锌酸根离子的表面浓度(非本体溶液浓度)逐渐增加,导致活化极化的产生.这几个因素促使电极反应区域(reaction zone)不断沿反应前沿方向推进.在不到30%的放电深度下,电极表面附近的金属锌已耗尽,这个区域的传递电流为零,成为了电极的一个“负载”.随着放电深度的增加,锌耗尽区域不断扩大,反应区域深入电极内部.

本文中,我们使用“均匀性”一词定性地衡量传递电流密度的分布状态.根据电极的放电规律,传递电流在任一时刻都集中于一个反应区域中,但随着电极参数的不同分布曲线形状各异,一般类似于正弦波.某一时刻,若反应区域内传递电流密度的波形的半峰全宽(FWHM)较大,说明传递电流密度的变化率较缓,峰值较低,描述为传递电流密度分布均匀;反之则反应区域内传递电流密度变化剧烈,峰值较高,描述为其分布不均.

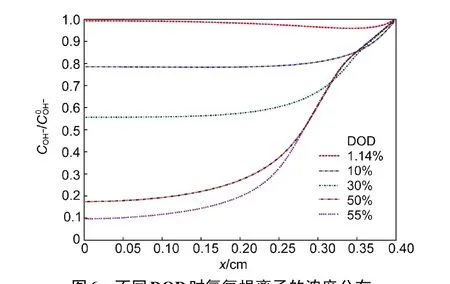
图6 不同DOD时氢氧根离子的浓度分布Fig.6 Distribution of hydroxyl ion concentration at different DOD

图7 不同DOD时传递电流密度(j)的分布Fig.7 Distribution of transfer current density(j)at different DOD

很明显,图7中各时刻传递电流密度的分布呈高度的不均匀性,在某一时刻一个非常狭小的区域提供了绝大部分的电流.这一特征加大了电极内部离子浓度分布的差异,以及相应的极化程度,对发挥电极性能产生了负面影响.

随着电极的运行,氢氧根离子逐渐消耗而锌酸根离子不断生成,导致固体氧化锌开始在电极内析出.其对电极性能影响巨大.锌酸根离子的析出会在电极表面形成一层疏松的多孔状膜,文献中一般称之为第一类钝化膜.这类膜多为白色多孔状结构,它一般不会对电极内部的物质传输过程造成影响.但当第一类钝化膜在电极内聚集,也有可能直接在电极颗粒表面生成第二类钝化膜.这类钝化膜的结构紧致,颜色由亮灰到黑色.29-31它会严重地限制电极内部的物质传输过程,导致局部氢氧根离子耗尽进而造成电极失效.

第二类钝化膜的生成机制32-34与第一类不同,它由氢氧化钾直接析出生成:

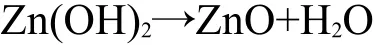
上式决定了这类膜生成条件的复杂性,包括:氢氧根离子在局部几乎耗尽或局部CZn(OH)42−

/COH−

的比值超过了一定的临界值.这两个条件常产生自非常高的阳极电流密度.另外如前所述,当第一类膜的厚度超过一定的值,也有可能限制离子传输从而生成第二类钝化膜.第二类钝化膜的生成机制也决定了锌电极不适宜在很高的电流密度下工作,如作为汽车的点火电源.本文中模拟了第一类膜的生成,而由于第二类膜生成的极端条件,目前通过实验尚未完全揭示其生成机理,模拟中也未见相关研究.

图8给出了电极内部固体氧化锌的体积分数分布及电极的孔隙度分布.从图中可以看出,一旦氧化锌固体开始形成,则只会越聚越多,这说明只要边界条件等外部因素不改变,一旦电极内的固体氧化锌开始析出,则难以溶解,只会继续增加.进而电极的失效是必然的.固体氧化锌对电极的损害还表现在:增加电极的电阻率,从而增加电能损耗;导致电极发热,这种欧姆热是电池温度升高的主要因素;另外,氧化锌有可能会包裹住锌颗粒,使其钝化不能参与电极反应,造成电极容量的损失.

基于以上各图及针对多组电极参数组合的模拟,我们对氧化锌影响电极性能的过程进行更深入的分析.从图5和图6可以发现,每种离子在电极内部的分布趋势差别较大,大约都以x=0.32−0.35 cm这个狭小的区域分界,而这一区域正是固体氧化锌最为集中的区域(图8).多组模拟都验证了这个规律.可见,由于固体氧化锌对传质过程的限制作用,电极内离子的分布规律将受到氧化锌集中析出位置的显著影响.从图6可以看出,在氧化锌集中区域的内侧,氢氧根离子浓度显著降低,对应于高的浓差极化过电位.很自然地我们可以猜测,如果氧化锌的集中区域靠近集流体一侧,那么传质受限区域将会减小,相应地电极性能的下降幅度也会减小.另一方面,如果氧化锌在电极内的析出时间推迟,其对电极性能的限制也将减小.通过比较不同电极参数的模拟情况可以验证,性能好的电极氧化锌的析出时间更晚,其析出位置也更靠近集流体一侧.

氧化锌的生成会限制了电极性能,但并不是体现为完全堵塞电极的孔隙结构进而隔绝了传质过程引起电极的失效.模拟结果显示,即使在电极失效时其最小孔隙度也远大于零,图8中最小孔隙度约为52%.比较不同时刻的浓度图(图5、图6)及氧化锌体积分布图(图8)可以看出,固体氧化锌并不是一析出就开始限制电极的传质过程,实际上锌电极中一般加入少量固体氧化锌以抑制电极的析氢过程.这说明氧化锌积累到一定程度才开始影响电极的传质过程,我们将其定义为一个临界值.当氧化锌的体积分数小于该临界值时,电极内部的传质过程不会受到显著影响,仅由于氧化锌的存在造成电极欧姆极化的增加,表现为图3中过电位曲线线性增加的第3部分;当氧化锌的体积分数超过该临界值后,电极的传质过程开始受限并不断加剧,直至电极失效.表现为图2的第4部分.对多组参数组合的电极进行模拟发现该临界点大约在30%−35%之间,即固体氧化锌的体积分数超过该范围后开始明显限制电极内部的传质过程,也标志着电极失效阶段的开始.

图8 不同DOD时电极孔隙度/固体氧化锌体积分数的分布Fig.8 Distribution of electrode porosity/volume fraction of ZnO at different DOD

结合前面所述二类氧化锌钝化膜的生成机制,我们可以认为当氧化锌的体积分数小于临界区域(εZnO=30%−35%)时,锌电极内生成的是第一类钝化膜,而当其大于临界区域后,第一类钝化膜的量已经足够大,以致开始限制电极内的质量传输过程,进而导致了第二类氧化锌钝化膜的生成.

4.2 电极优化设计

锌电极的设计过程中需要考虑多个因素,如电极的孔隙度、厚度、电解液组分、浓度等.一般来说,电解液的电导率越高相应的电极性能越好.

图9显示了几种不同参数组合所对应电极的过电位曲线.其中ε0=0.5,L=0.1,0.2,0.3 cm的三个电极容量分别接近ε0=0.73,L=0.2,0.4,0.6 cm的三个电极.通过比较可以观察同样容量的电极改变孔隙度及厚度后的性能变化,以及相同孔隙度的电极性能随厚度(容量)的变化.第四条曲线的电极参数为ε0=0.5,L=0.3 cm,但其溶液电导率提高到10倍.这里选取的两个孔隙度ε0=0.5,0.73分别对应于Sunu8,9及Mao12等的模拟,因而本文的模拟结果也可以与其进行比较.

从图9中可以看出,容量相同的情况下,孔隙度大的电极能达到更大的放电深度;提高溶液电导率也会提高最大放电深度,从而增加电极材料利用率.

对于同样的孔隙度,可以看出随着电极厚度即容量的增加其放电深度(材料利用率)有很大的降低.Mao等12针对一次电池的模拟结果显示,锌电极厚度分别为0.2、0.4、0.5 cm时电极所能达到的放电深度几乎没有差别,值得注意的是其所采用的工作电流密度为 20 mA·cm−2,远比本文模拟(50 mA·cm−2)的小.我们采用本文的模型模拟了参数为ε0=0.5,L=0.1,0.2,0.3 cm的三个电极在工作电流密度为10 mA·cm−2的条件下的放电行为,结果也显示其最大放电深度相差无几.当放电到计算程序设定的最大放电深度(80%)时,锌电极的过电位也很小,约为70 mV.

图9 不同电极的过电位曲线比较Fig.9 Comparison of overpotentials of different electrodes

两种工作条件下电极行为的显著差异反映锌电极对于工作电流的敏感性.实际使用中即表现为一次性锌电极与动力电池用锌电极截然不同的放电规律.这种差异性可解释如下.当电极的工作电流密度较小时(20 mA·cm−2以下),放电过程中电极内部传递电流密度的分布较为均匀,反应区域稳定向电极内部推进,氧化锌的生成时间较迟,速率较慢且集中分布位置更靠近集流体一侧,在电极工作的大部分时间里生成的都是第一类氧化锌钝化膜,不会明显限制离子的传输.相应地,锌电极的过电位较低,电池的电势降主要来自正极(空气电极);而作为动力电源使用时,锌电极的工作电流密度约为50 mA·cm−2或更大,放电过程中传递电流密度的分布高度不均匀化(一般为一个尖锐的波峰),峰值很高,导致局部电极极化严重,很快生成第一类氧化锌钝化膜,当其体积分数超过临界区域后开始限制传质过程,逐渐生成第二类氧化锌钝化膜,在电极其它部分的活性材料还没有充分反应的情况下就导致电池失效.

由此可见传递电流密度分布均匀程度的重要性.若传递电流密度分布均匀,则即使在大电流条件下工作,局部的最大值也有限,局部极化程度及离子的浓度变化就较缓和,第二类钝化膜的生成也会延迟,电极的材料利用率就会提高.

传递电流密度的分布受多个因素的影响,最重要的即工作电流密度,其它因素如电极厚度、孔隙度、溶液浓度等.前几个因素与电极的设计规格相关,无法在电极的工作过程中更改.电极内的溶液浓度则不然,可通过技术手段进行动态调节.在试验中为保持锌电极的“富液”环境有时需向其补充氢氧化钾溶液,这一措施可有效延缓电极失效时间,提高电极材料的利用率.另一方面,我们知道第二类钝化膜的生成会限制电极内部的质量传输过程,从而引起电极失效,那么如果人为地向传质受限区域注入氢氧化钾溶液,部分地抵消钝化膜的限制;甚至将氧化锌溶解,电极性能应该会回升.基于此,本文模拟了补液情况下电极的性能变化情况.即选取图9中性能最差的参数组合:ε0=0.5,L=0.3 cm,在30%−40%DOD的放电阶段持续向电极补充氢氧化钾溶液,使其维持在初始浓度.从图10的模拟结果可以看出,在开始补液后过电位有一个突降,这是由于补液消除了部分浓差极化,并提高了溶液的离子电导率造成的.补液的过程中电极的过电位一直维持在一个很低的值上,说明了氢氧根离子浓度的重要性.结束补液之后过电位急剧上升,并很快失效,表明补液并没有从根本上改变电极内部环境.比较固体氧化锌的分布可知其值并没有降低,可见补液并没有溶解氧化锌.若要从根本上使电极性能好转,需要将电极内的氧化锌溶解,可持续向电极内注入高浓度的碱液,同时从边界上引出电极反应生成的锌酸根离子,以促使氧化锌重新溶解为锌酸根离子.

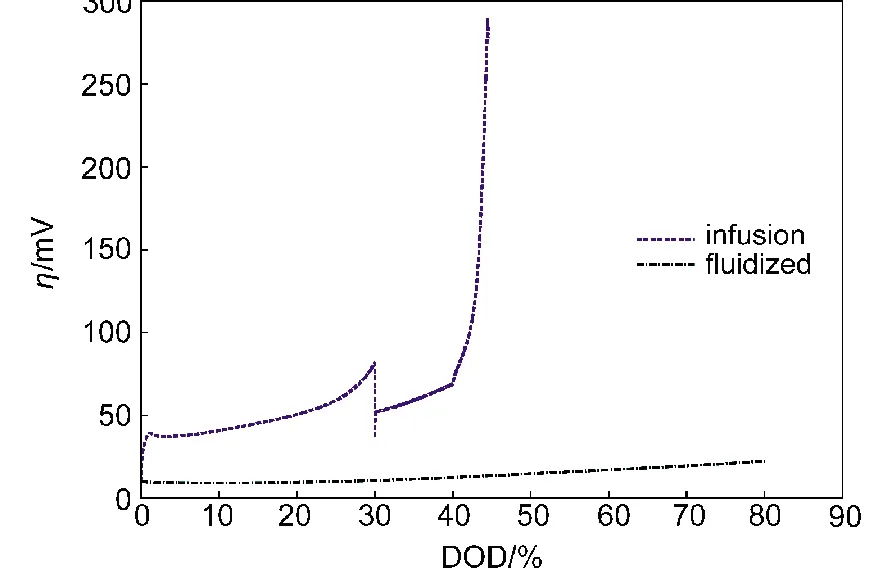
图10 优化后的电极过电位曲线Fig.10 Overpotential curves of optimal electrodes

另一个理想的设计是,保持电极内氢氧根离子与锌酸根离子的浓度为定值,则固体氧化锌将不可能析出,从而电极内部始终维持一个良好的溶液环境.Colborn等35的专利设计了一个流动体系,作为电极材料的锌颗粒与电解液是循环的.通过这种设计使电解液中的离子浓度保持为定值,且消除了氧化锌生成的可能性.因而这种结构的锌-空气电池能够充分地利用锌材料.本文通过将方程组中的离子浓度设为定值而模拟了其它物理量的分布变化.从图10中第二条曲线可以看出,离子浓度恒定情况下的电极过电位非常小,放电过程可一直持续到锌活性材料耗尽(图中放电至80%是由于该值是计算程序设定的最大放电深度).图11显示了此条件下传递电流密度的分布变化情况.明显地,图中传递电流密度分布比图7中的更均匀,峰值更小,相应地各物理量在反应区域内的变化也很平缓,从而各类极化作用较小.这也说明了传递电流密度的集中分布对于电极性能的发挥是不利的.

图11 离子浓度恒定条件下不同DOD时传递电流密度的分布Fig.11 Distribution of transfer current density at different DOD with constant ion concentrations

5 结论

本文针对大功率锌电极的放电过程建立了一维数学模型.考虑到控制方程组中方程的不同数学性质,采用解耦算法对其进行了求解,提高了求解效率.借助数值结果模拟了锌电极的放电规律,失效机制及优化方法.分析了固体氧化锌的析出对于电极内部传质过程的限制过程,如其析出时间及集中分布区域.以及固体氧化锌的体积分数对于电极性能的影响.模拟结果表明:

(1)交换电流密度在电极内部的分布不均匀,且工作电流密度的加大会加剧这种不均匀性.

(2)固体氧化锌的析出所生成的第一类钝化膜会继续聚集,逐渐生成致密的第二类钝化膜,限制质量传输过程,导致电极失效.钝化膜由第一类向第二类的转变大概以30%−35%的体积分数为分界区域.

(3)锌电极运行过程中最重要的是保持电极内部良好的溶液环境,在固体氧化锌已经开始限制电极性能的条件下补液的措施可以延迟电极的失效时间;采用开放式的电极设计方法,驱动电解液循环流动可以将离子浓度保持在一个稳定的范围内,从而消除固体氧化锌的生成以最大限度地利用锌电极材料.这是锌电极中材料利用率最高的一种设计方式,但同时也损失了锌电极密闭便携的特点.

本文建立的数学模型是一维的,其结果可以帮助我们非常直观地了解锌电极的放电规律,也便于与实验结果进行直接对照.由于锌电极在厚度方向远小于其它两个方向的尺度,本文针对电极厚度方向的一维模型对于电极过程是一个非常合理的近似.若需要了解其它两个方向上物理量的变化情况,就应建立二维或三维模型.这需要更多的物性参数,如各个方向的传质系数、电导系数等.相对高维模型所带来的计算量的增加,物性参数的测量是一个更值得注意的问题.而这方面的工作目前非常有限.同样地,对于单电池,电极内的温度变化可以忽略,相反,对于电堆设计,温度是一个必须加以重视的因素.但目前锌电极温度过程的计算模拟中所需的物性参数大部分仍缺乏可靠的实验值,如氢氧化钾溶液/锌酸钾溶液的密度、比热容、热传导系数等.由此可见,物性参数实验测量值的缺乏是目前锌电极过程数值模拟尤其是其热特性研究中面临的一个关键问题.

致谢: 感谢贺缨教授对本文提出的宝贵的修改意见.

(1) Brodd,R.J.;Bullock,K.R.;Leising,R.A.;Middaugh,R.L.;Miller,J.R.;Takeuchi,E.Journal of the Electrochemical Society 2004,151,K1.

(2) Sapkota,P.;Kim,H.Journal of Industrial and Engineering Chemistry 2009,15,445.doi:10.1016/j.jiec.2009.01.002

(3) Goldstein,J.R.;Gektin,I.;Koretz,B.Electric FuelTMZinc-Air Battery Regeneration Technology;In The 1995Annual Meeting of theApplied Electrochemistry Division of the German Chemical Society,Duisburg,Germany,Sept 27−29,1995.

(4) Ou,X.Q.;Liang,G.C.Battery Bimonthly 2006,36,274.[欧秀芹,梁广川.电池,2006,36,274.]

(5) Li,F.;Xu,X.Z.;Song,H.;Xiong,J.;Wu,F.Acta Phys.-Chim.Sin.2009,25(11),2205.[李 芬,徐献芝,宋 辉,熊 晋,吴 飞.物理化学学报,2009,25(11),2205.]doi:10.3866/PKU.WHXB20091119

(6) Li,S.Z.;Sun,L.;Hu,R.G.;Wang,Z.L.;Zhang,X.G.;Lin,C.J.Acta Phys.-Chim.Sin.2009,25(8),1635.[李思振,孙 岚,胡融刚,王志林,章小鸽,林昌健.物理化学学报,2009,25(8),1635.]doi:10.3866/PKU.WHXB20090804

(7) Choi,K.W.;Bennion,D.N.;Newman,J.Journal of the Electrochemical Society 1976,123,1616.doi:10.1149/1.2132657

(8) Sunu,W.G.Transient and Failure Analyses of Porous Zinc Electrodes;University of California:Los Angeles,1978.

(9) Sunu,W.G.;Bennion,D.N.Journal of the Electrochemical Society 1980,127,2007.doi:10.1149/1.2130054

(10) Isaacson,M.J.;McLarnon,F.R.;Cairns,E.J.Journal of the Electrochemical Society 1990,137,2014.doi:10.1149/1.2086856

(11) Podlaha,E.J.;Cheh,H.Y.Journal of the Electrochemical Society 1994,141,15.

(12) Mao,Z.Journal of the Electrochemical Society 1992,139,1105.doi:10.1149/1.2069348

(13) Venkatraman,M.;Vanzee,J.Journal of Power Sources 2007,166,537.doi:10.1016/j.jpowsour.2006.12.064

(14) Torabi,F.;Aliakbar,A.Journal of the Electrochemical Society 2012,159,A1986.

(15) Zhang,X.G.Corrosion and Electrochemistry;Metallurgical Industry Press:Beijing,2008;pp 491,463,464.[章小鸽.锌的腐蚀与电化学.北京:冶金工业出版社,2008:491,463,464.]

(16) Sunu,W.G.;Bennion,D.N.Journal of the Electrochemical Society 1980,127,2007.doi:10.1149/1.2130054

(17) Bockris,J.O.;Nagy,Z.;Damjanovic,A.Journal of the Electrochemical Society 1972,119,285.doi:10.1149/1.2404188

(18) Butler,J.N.Ionic Equilibrium:A Mathematical Approach,10th ed.;Addison-Wesley:Reading,MA,1964.

(19) Boden,D.P.;Wylie,R.B.;Spera,V.J.Journal of the Electrochemical Society 1971,118,1298.doi:10.1149/1.2408309

(20) Kong,X.Y.Advanced Mechanics of Fluids in Porous Media;University of Science and Technology of China Press:Hefei,1999.[孔祥言.高等渗流力学.合肥:中国科学技术大学出版社,1999.]

(21) Kriegsmann,J.Journal of Power Sources 1999,84,52.

(22) Kordesch,K.V.In Batteries,Manganese Dioxide;Marcel Dekker:New York,1974;p 348.

(23) Newman,J.;Thomas-Alyea,K.E.Electrochemical Systems;Wiley:Hoboken,New Jersey,2012;p 303.

(24) Um,S.;Wang,C.;Chen,K.S.Engineering Sciences 2000,147,4485.

(25) Wang,C.Journal of Power Sources 2002,110,364.doi:10.1016/S0378-7753(02)00199-4

(26) Tao,W.Q.Nemerical Heat Transfer,2nd ed.;Xiʹan Jiaotong University:Xiʹan,2001.[陶文铨.数值传热学.第二版.西安:西安交通大学出版社,2001.]

(27) Versteeg,H.K.;Malalasekera,W.An Introduction to Computational Fluid Dynamics:the Finite Volume Method;Pearson Education Limited:New Jersey,2007.

(28) Moré,J.J.;Garbow,B.S.;Hillstrom,K.E.User Guide for MINPACK-1,CM-P00068642,1980.

(29) Powers,R.W.;Breiter,M.W.Journal of the Electrochemical Society 1969,116,719.doi:10.1149/1.2412040

(30) Powers,R.W.Journal of the Electrochemical Society 1971,118,685.doi:10.1149/1.2408145

(31) Powers,R.W.Journal of the Electrochemical Society 1969,116,1652.doi:10.1149/1.2411652

(32) Liu,M.;Cook,G.M.;Yao,N.P.Journal of the Electrochemical Society 1981,128,1663.doi:10.1149/1.2127707

(33) Cabot,P.L.;Cortes,M.;Centellas,F.;Perez,E.Journal of Applied Electrochemistry 1993,23,371.doi:10.1007/BF00296694

(34) Cabot,P.L.;Cortes,M.;Centellas,F.A.;Garrido,J.A.;Perez,E.Journal of Electroanalytical Chemistry and Interfacial Electrochemistry 1986,201,85.doi:10.1016/0022-0728(86)90089-6

(35) Colborn,J.A.;Wright,K.A.;Gulino,R.Method andApparatus for Refueling an Electrochemical Power Source.US Patent 5952117,1999.