中考数学合情推理能力的题型析解

山东省宁阳县教育局教科研中心 尚延亮 （邮编：271400）

合情推理是从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果.在解决问题的过程中，合情推理能产生新知识、新思想、新理论.可见，在某些情况下，教学生合情推理、教会学生猜想，远比教学生论证推理与教证明要有意义得多.最近几年的数学中考命题者们在这方面进行了有益而大胆的探索，试卷中出现了一些引导学生进行合情推理题目，本文从2013年各地的中考试卷中选择部分有代表性的题目进行分析.希望对指导老师们的教学有所启迪.

1 与数形结合思想联系在一起，考查学生类比推理的能力

例1 （重庆卷第10题）下列图形（如图1所示）都是由同样大小的矩形按一定的规律组成，其中第（1）个图形的面积为2cm2，第（2）个图形的面积为8cm2，第（3）个图形的面积为18cm2，…，则第（10）个图形的面积为（ ）.

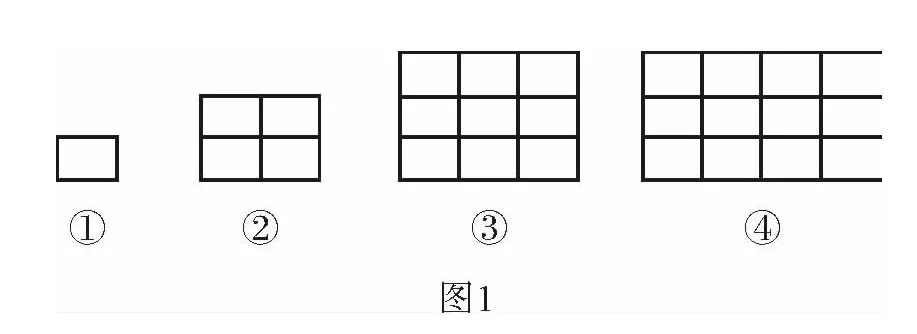
A.196cm2B.200cm2

C.216cm2D.258cm2

解析 本题创设了一个探究图形个数的“数形结合”的数学模型，考查了与图形面积有关的规律探究问题，解答时，需要从简单到复杂进行探究：图中每一个小矩形的面积为2cm2，

第（1）个图形的面积为2＝2×12（cm2）；

第（2）个图形的面积为8＝2×22（cm2）；

第（3）个图形的面积为18＝2×32（cm2）；

第（4）个图形的面积为32＝2×42（cm2）；

……

由此，可以类比猜想得到规律：第10个图形的面积为2×102＝200（cm2）.故选B.

点评 类比推理是根据两个或两类对象有部分属性相同，从而推出它们的其他属性也相同的一种推理.它是一种常用的合情推理形式.

从分析的过程看，本题是借助于“图形”的形象性与直观性逐步得到最终解决的.本题除了考察学生的类比猜想能力外，还渗透了数形结合的思想，使复杂问题简单化，抽象问题具体化，化难为易，获得简便易行的成功方案.本题给我们的启发有二：一是在数学学习中，当遇到一个问题涉及到很多或无穷多情形时，我们可以从问题的简单情形或特殊情形入手，通过简单情形或特殊情形的试验，从中发现一般规律或作出某种猜想，从而找到解决问题的途径.二是在教学中，千万不要就知识点而讲知识点，一定要把这些“显知识”背后所“隐含”的数学思想揭示出来.做到用数学思想方法来“统领”知识点，以达到优化知识结构的目的，因为只有这样被“优化”起来的知识结构才具有生命力和创造性.

2 在算式的计算中，考查学生归纳猜想规律的能力

例2 （山东省滨州卷第18题）观察下列各式的计算规律过程：

5×5＝0×1×100＋25，

15×15＝1×2×100＋25，

25×25＝2×3×100＋25，

35×35＝3×4×100＋25，

……

请猜测，第n个算式（n为正整数）应表示为＝________.

解析 本题以简单的整数计算为载体，以考查学生归纳猜想的能力为主.观察给定的4个算式可以发现，等式的左边都是［10（n－1）＋5］×［10（n－1）＋5］，等式的右边都是（n－1）×n×100＋25，即100n（n－1）＋25，所以第n个算式（n为正整数）应表示为［10（n－1）＋5］×［10（n－1）＋5］＝100n（n－1）＋25.

点评 归纳推理是从特殊到一般的推理，归纳推理是一种合情推理.给定几个代数计算式子，在计算的过程中通过归纳、猜想得到有关的规律，然后用代数变形的方式求某个式子的值或证明猜想的正确性，并利用归纳得到的规律解答给定的问题是一种常见的题型，解答这样的问题需要较强的观察能力、分析判断能力、类比归纳等能力.在教学过程中，教师应结合具体的教学内容，经常设计一些类似的题目让学生去分析和思考，学生的归纳猜想能力，必将得到较大的提高.

3 考查学生用统计的知识进行估算的能力

例3 （广东卷第20题）某校教导处为了解该校七年级同学对排球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情况（每位同学必须且只能选择最喜爱的一项运动项目），进行了随机抽样调查，并将调查结果统计后绘制成了如表1和图2所示的不完整统计图表.

（1）请你补全下列样本人数分布表（表1）和条形统计图（图2）；

（2）若七年级学生总人数为920人，请你估计七年级学生喜爱羽毛球运动项目的人数.

表1 样本人数分布表

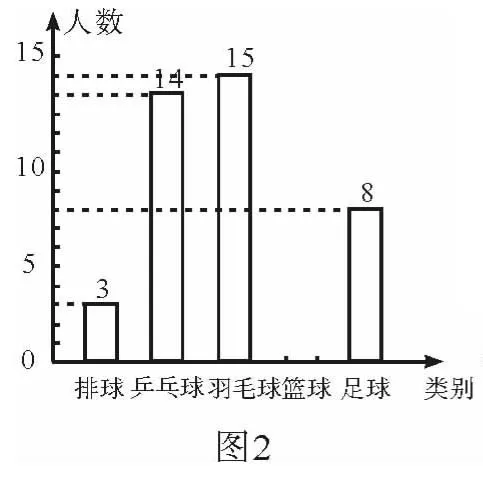
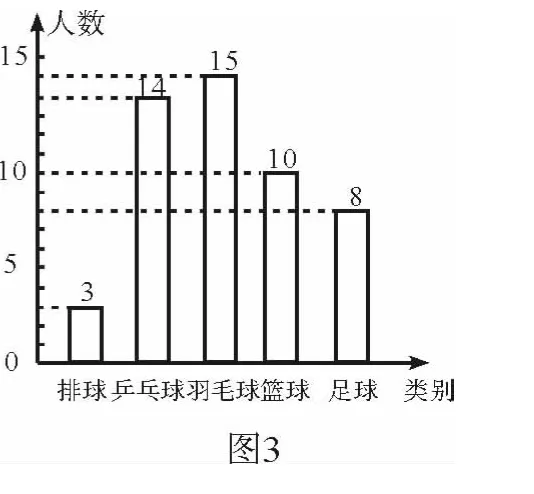
解析 （1）羽毛球占的百分比为100%－6%－28%－20%－16%＝30%，调查的人数为15÷30%＝50.所以喜欢篮球的人数为50×20%＝10.补全条形统计图如图3所示.（2）用样本估计总数，得920×30%＝276（人）.即七年级学生喜爱羽毛球运动项目的约有276人.

点评 统计推理是用样本的资料对总体的某些性质进行估计或推断的不完全归纳推理.统计推理是从样本到总体的推理，是一种常用的统计推理.

本题以学生感兴趣球类运动进行调查为载体，得到了一些基本数据，主要考察同学们对基本统计概念的理解情况，对给定样本数据进行处理的能力以及用样本属性估计总体属性的能力.要求同学们能掌握这些概念和计算方法，正确理解样本数据的特征，能根据计算结果作出准确的判断.用样本估计总体是中考对“统计初步”知识考查的题型之一，求解的方法是用总体乘以考察对象在样本中所占的比例.类似这样的问题对于培养学生“通过分析数据作出判断”的能力是非常有益的.

4 在解答探索型问题的过程中，考查学生的合情推理能力

例4 （云南省八地市卷23题）如图4，四边形ABCD是等腰梯形，下底AB在x轴上，点D在y轴上，直线AC与y轴交于点E（0，1），点C的坐标为（2，3）.

（1）求A、D两点的坐标；

（2）求经过A、D、C三点的抛物线的函数关系式；

（3）在y轴上是否存在点P，使△ACP是等腰三角形？若存在，请求出满足条件的所有点P的坐标；若不存在，请说明理由.

分析 （1）根据E、C两点的坐标求直线EC的解析式，进而求出点A的坐标，由点C的坐标可得到点D的坐标.（2）根据A、D、C三点的坐标，用待定系数法求出抛物线的解析式.（3）观察图形，可以猜想到在y轴上存在点P，使△ACP是等腰三角形.而且这样的点P有多个.

解 （1）、（2）省略.

（3）存在.

①作线段AC的垂直平分线，交y轴于点P1，交AC于点F，如图5所示.

由OA＝OE，△OAE为等腰直角三角形，∠AEO＝45°，

求得 ∠FEP1＝∠AEO＝45°，所以△FEP1为等腰直角三角形.

②以点A为圆心，线段AC长为半径画弧，交y轴于点P2、P3.可求得圆的半径长AP2＝AC＝3.连接AP2，则在Rt△AOP2中，

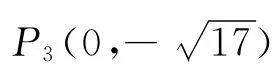
③以点C为圆心，线段CA长为半径画弧，交y轴于点P4、P5，则圆的半径长CP4＝CA＝3，在Rt△CDP4中，CP4＝ 3，CD＝2，，

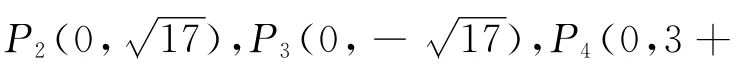
点评 本题是以三角形为载体的探索型问题.所谓探索型问题就是问题的条件或结论不直接给出，需要经过观察、分析、分类、推理、化归、特殊化、一般化、数形结合及猜想等一系列的探索活动，才能完成解答.解答这样的问题，需要学生具有一定的阅读理解能力，比较强的综合分析与判断猜想能力.

就本题而言，前两问比较容易，第三问是需要探索的问题，解答的关键在于能凭借直观猜想到存在这样的点P使△ACP是等腰三角形，然后通过作图探究点P的坐标.

总之，我们在教学中要夯实基础知识、渗透常见的思想方法，通过分析、综合，把所学的知识序列化、结构化.养成勤于思考、善于猜想的良好习惯，强调、重视论证推理的同时，强化合情推理的教育.精心设计教学，结合具体的教学内容，对教学内容进行二次改造，按照“问题情境—建立模型—求解验证”的思路引导学生进行观察、实验、分析、比较、联想、类比、归纳素材，以培养学生的数学猜想意识、猜想习惯、猜想能力.让同学们在经历观察、试验、猜测、验证、推理与交流的过程中，体验数学知识的形成过程.